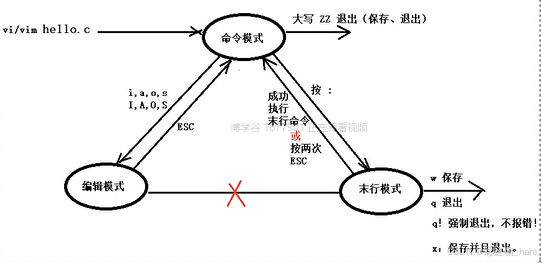
就会一个，是退步了还是太难了。

远看是个RSA，近看不是，只用的分解n

from sympy import isprime
from sympy.ntheory import legendre_symbol
import random
from Crypto.Util.number import bytes_to_long

k=79    #<-- i couldn't stress more

def get_p():
    global k
    while True:
        r=random.randint(2**69,2**70)
        p=2**k*r+1
        if isprime(p):
            return p
        else:
            continue

def get_q():
    while True:
        r=random.randint(2**147,2**148)
        q=4*r+3
        if isprime(q):
            return q
        else:
            continue


def get_y():
    global n,p,q
    while True:
        y=random.randint(0,n-1)
        if legendre_symbol(y,p)==1:
            continue
        elif legendre_symbol(y,q)==1:
            continue
        else:
            return y


flag=b'DASCTF{redacted:)}'
flag_pieces=[flag[0:10],flag[11:21],flag[22:32],flag[33:43],flag[44:]]
#assert int(bytes_to_long((flag_pieces[i] for i in range(5)))).bit_length()==k

p=get_p()
q=get_q()
n=p*q
print(f'{n=}')

y=get_y()
print(f'{y=}')


def encode(m):
    global y,n,k
    x = random.randint(1, n - 1)
    c=(pow(y,m,n)*pow(x,pow(2,k),n))%n
    return c

cs=[]
for i in range(len(flag_pieces)):
    ci=encode(bytes_to_long(flag_pieces[i]))
    cs.append(ci)

print(f'{cs=}')

'''
n=542799179636839492268900255776759322356188435185061417388485378278779491236741777034539347
y=304439269593920283890993394966761083993573819485737741439790516965458877720153847056020690
cs=[302425991290493703631236053387822220993687940015503176763298104925896002167283079926671604, 439984254328026142169547867847928383533091717170996198781543139431283836994276036750935235, 373508223748617252014658136131733110314734961216630099592116517373981480752966721942060039, 246328010831179104162852852153964748882971698116964204135222670606477985487691371234998588, 351248523787623958259846173184063420603640595997008994436503031978051069643436052471484545]
'''

先是生成p,q其中p = 2**k*r + 1 这个r只有70位，一下coopersmith就行。

###################1, coppersmith求p    p = 2^79*x + 1
k = 79
P.<x> = PolynomialRing(Zmod(n))
f = 2^k*x + 1
res = f.monic().small_roots(X=2^70, beta=0.499, epsilon=0.02)
#[1040145546891496498175]
p = int(f(res[0]))
#628729403897154553626034231171921094272614401

然后是生成y这个y对p,q都不是二次剩余(拉格朗日符号不为1)

把flag分成5块每块10字节（79位，与k相同）

c = y^m * rand^(2^k) % n 

这里边由于y对p不是二次剩余，那么如果m为奇数c就不是二次剩余，如果是偶数就是，可以用jacobi符号判断。

然后如果是奇数就除去y再开根号。而后边的rand^(2^k)保证开足够的根号（79）依然是二次剩余

这里有两个小坑，虽然c是模n的，但jacobi符号需要用素数运算，所以这里只能用一个因子来计算。第2是开根号有两个根，需要递归遍历下。

###################2, 二次剩余 求m
#每段flag只有79位， c = y^m * rand^(2*79)
#如果对p是二次剩余 m为0,c开根号            c2 = y^(m    //2)*rand^(2^78)
#否则m为1，c/y再开根号                     c2 = y^((m-1)//2)*rand^(2^78)
from gmpy2 import jacobi,invert 

def rabin(c):
    P.<x> = PolynomialRing(GF(p))
    f1 = x^2 - c
    resp = f1.roots()
    return [int(i[0]) for i in resp]

def getm(c,m):
    global ok,flag
    if ok: return 
    
    #print('Try:',c,m)
    if len(m)>=k:
        print('OK',m, long_to_bytes(int(m,2)))
        flag += long_to_bytes(int(m,2))
        ok = True
        return
    
    if jacobi(c, p) == -1:
        m = '1'+m
        c = int(c*invert(y,p)%p)
    else:
        m = '0'+m
    cs = rabin(c)
    for tc in cs:
        getm(int(tc),m)

flag = b''
for tc in cs:
    ok = False
    getm(tc,'')

print(flag)
#DASCTF{go0_j06!let1sm0v31n_t0_th3r_chanlenges~>_<}