目录
1 关于二项分布的基本内容
2 二项分布的概率
2.1 核心要素
2.2 成功K次的概率,二项分布公式
2.3 期望和方差
2.4 具体试验
2.5 概率质量函数pmf 和cdf
3 二项分布的pmf图的改进
3.1 改进折线图
3.2 如何生成这种竖线图呢
4 不同的二项分布
4.1 p=0.5的时候,正的二项分布,像正态部分
4.2 p=0.2的时候,左偏的二项分布
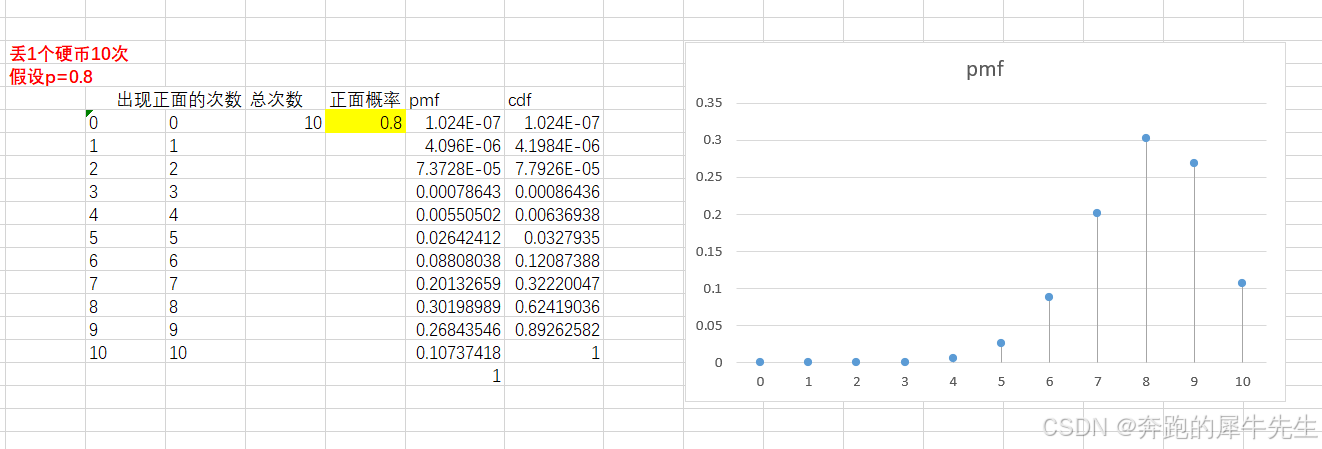
4.3 p=0.8的时候,右偏的二项分布
1 关于二项分布的基本内容
如下

2 二项分布的概率
2.1 核心要素
- 离散的
- 伯努利试验,试验结果可以归类成A,非A
- A类概率 P
- 总试验次数 N
- 成功k次 K
2.2 成功K次的概率,二项分布公式
- 成功K次的概率
- 展开用数学公式计算: C(N,k)*P^k*(1-p)^(n-k) =COMBIN(J$5,I5)*K$5^I5*(1-K$5)^(J$5-I5)
- 用EXCEL封装的公式计算: BINOM.DIST(I5,J$5,K$5,0)
2.3 期望和方差
- 期望 E=n*p
- 方差 VAR=n*p*(1-p)
2.4 具体试验

2.5 概率质量函数pmf 和cdf
- 离散的只有pmf,没有pdf.
- 所以下面的这个图是连续的,有误导性
- 虽然内容是正确的,但不能生成曲线,只能是离散的断点

3 二项分布的pmf图的改进
3.1 改进折线图
- 直接用次数K 和 pmf 画图,这样
- 需要把次数修改为文本就好了,比如用 =""&h1 这样

3.2 如何生成这种竖线图呢
- 双击图形
- 呼出菜单,图表设计
- 最左上角,点击,添加图表
- 线条里可以添加 竖线
- 然后可以设置曲线的透明图为100%搞成看不见即可


4 不同的二项分布
4.1 p=0.5的时候,正的二项分布,像正态部分

4.2 p=0.2的时候,左偏的二项分布

4.3 p=0.8的时候,右偏的二项分布