全文链接:https://tecdat.cn/?p=38496
分析师:Pengyuan Wen
在当今经济研究与商业决策领域,精准的时间序列预测具有极为关键的意义。社会消费品零售总额作为反映人民消费水平以及国民经济状况的核心指标,其发展趋势的精准把握对中国经济高质量发展转型意义非凡。同时,在预测技术的发展进程中,循环神经网络(RNN)逐渐崭露头角,成为具有竞争力的预测方法,然而传统的指数平滑(ETS)和自回归移动平均(ARIMA)等统计模型,凭借其高精度、稳健、高效且自动化的特性,在非专业用户群体中仍占据重要地位(点击文末“阅读原文”获取完整代码数据)。
过往预测领域呈现两极化现象,神经网络曾因多种因素被部分从业者摒弃,且复杂新颖架构未充分对比单变量统计方法。本研究聚焦于此,以全国社会消费品零售总额数据为基础,深入探究乘积季节模型在其中的应用,并结合多源数据展开分析。同时,广泛研究不同的 RNN 架构、循环单元等,通过多数据集实验,涵盖 CIF 2016、NN5 等,对比 RNN 与传统模型,旨在为预测领域提供数据处理、模型构建与应用的全面指南,助力从业者提升预测效果与决策质量。
乘积季节模型的全国社会消费品零售总额的ARIMA建模分析
社会消费品零售总额是反映人民消费水平的重要度量指标,同时也是国民经济体系中的一个重要评价指标,因此,分析研究社会消费品零售总额的发展趋势对于转型期的中国经济高质量发展具有重要意义。
任务/目标
根据服装零售业务营销要求,运用多种数据源分析实现精准销量预测。
数据源准备
数据为从国家统计局官网收集的1998年1月至202年12月的不完整的(从2012年开始每年1月和2月的数据缺失)全国社会消费品零售总额数据。
缺失值填补
首先使用2011年12月之前的完整数据建立乘积季节模型,填补2012年的缺失值,再利用2012年12月之前的完整数据建立乘积季节模型,填补2013年的缺失值,以此类推……采用此逐年预测的方法补全所有的缺失值。
在对2011年12月之前的完整数据建立乘积季节模型的建模过程中,首先绘制了时序图,继而进行了ACF、PACF和ADF检验,发现其为带有明显上升趋势以及季节特性的非平稳序列,对其进行了一次和季节差分,差分后的序列平稳,继而进行系统建模,建模后进行残差分析以及查看q-q图,均通过了模型检验,最后进行用预测值补全缺失值的步骤。
模型建立
对1998年1月至2020年12月的完整数据绘制时序图,而后进行ACF、PACF和ADF检验,发现其为带有明显上升趋势以及季节特性的非平稳序列,对其进行了一次和季节差分,差分后的序列平稳,继而进行系统建模,最终通过三个模型对比,选定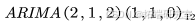 为最优模型,建模后进行残差分析以及查看q-q图,均通过了模型检验。
为最优模型,建模后进行残差分析以及查看q-q图,均通过了模型检验。
划分训练集和测试集
用选定的最优乘积季节模型结合2020年6月之前的数据,将其作为训练样本,对2020年6月至12月进行预测,并将其与真实数据进行对比,发现短期的预测效果很好。然后利用完整的2020年12月之前的数据与其对应的最优模型,对2021年1月至2021年6月的数据进行预测,并给出预测值上下限。
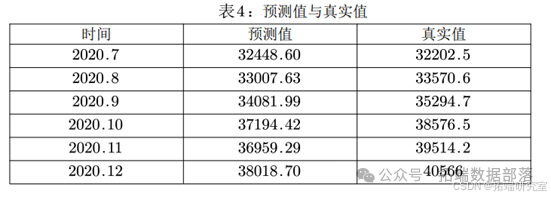
使用2020.6之前的数据作为训练样本,利用模型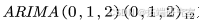 ,预留2020.7至2020.12的月度数据来进行预测结果的评估和展示,如下表,可以看出模型对短期的预测较符合实际情况,而长期预测上的表现并不是很好。
,预留2020.7至2020.12的月度数据来进行预测结果的评估和展示,如下表,可以看出模型对短期的预测较符合实际情况,而长期预测上的表现并不是很好。
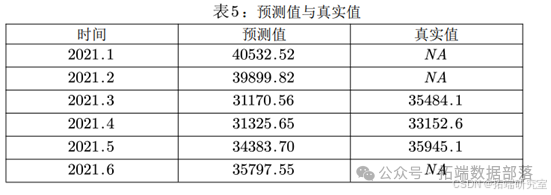
使用predict()函数预测2021.1至2021.6的数据,与真实数据值进行对比如下表,可以看出预测的效果不是很理想,在3月出现了很大的偏差。图中红线为预测值,蓝线为上下限
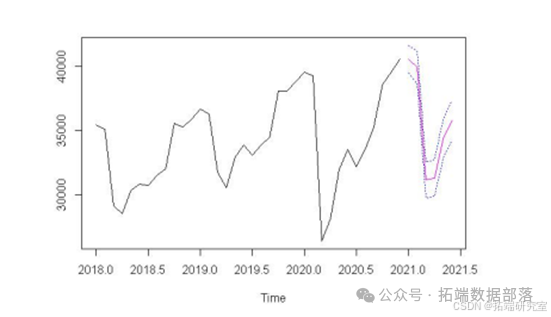
据此看来,带有季节特性的数据在用到季节模型或者乘积季节模型时,在其模型的建立过程中我需要有更好的理解与掌握。整体看来趋势上和实际值拟合情况较好,虽然这是利用学习的TSA手段挖掘出来的数据背后蕴含的规律与大趋势,但最后利用模型进行预测的结果却效果不佳,可能是消费品总额数据也收到政策或者市场自身特性的影响,使得很难做到精准的长期预测。
循环神经网络RNN、指数平滑ETS和、ARIMA模型时间序列预测|附数据代码
循环神经网络(RNN)已成为具有竞争力的预测方法,在近期 M4 竞赛的获胜方法中尤为显著。然而,诸如指数平滑(ETS)和自回归移动平均(ARIMA)等成熟的统计模型不仅因其高精度而广受欢迎,还因其稳健、高效且自动化而适用于非专业用户。在这些方面,RNN 仍有很长的路要走。我们进行了广泛的实证研究,并开发了用于预测的现有 RNN 架构的开源软件框架,这使我们能够制定其使用指南和最佳实践。例如,我们得出结论,如果数据集中的序列具有同质的季节性模式,RNN 能够直接对季节性进行建模,否则我们建议进行去季节化步骤。与 ETS 和 ARIMA 的比较表明,所实现的(半)自动 RNN 模型并非万能,但在许多情况下是具有竞争力的替代方案。
在预测领域的过往情况中,存在两种鲜明的表现。一方面,不少从业者因觉得神经网络(NN)缺乏竞争力而将其摒弃;另一方面,神经网络的爱好者们虽提出诸多复杂且新颖的神经网络架构,却大多未针对更为简易的单变量统计方法展开令人信服的实证评估。诸多时间序列预测竞赛,诸如 M3、NN3 和 NN5 竞赛(Makridakis 等人,2018b;Crone 等人,2011;Crone,2008)均支撑了这一观点,由此神经网络被视作不适用于预测(Hyndman,2018)。
过去神经网络表现欠佳,可能存在多种缘由。其一,单个时间序列往往过短,难以运用复杂方法予以建模。其二,时间序列的特征会随时间发生变化,即便长序列也可能因缺乏足够相关数据而无法拟合复杂模型。故而,若要运用复杂方法对序列建模,序列必须具备足够长度,且由相对稳定的系统生成。此外,神经网络还因黑箱特性而饱受诟病(Makridakis 等人,2018b)。所以,预测从业者向来倾向于选择更为直接的统计技术。
方法论
在本部分,我们将详细描述综合实验研究中所采用方法的细节。我们将介绍不同的循环单元类型、RNN 架构以及在研究中实现与比较的学习算法。
循环神经网络
我们的研究实现了多种 RNN 架构以及不同的 RNN 单元。接下来将详细解释。
循环单元
在文献提及的不同 RNN 单元中,我们选择以下三种类型的循环单元来构建实验中 RNN 的层。
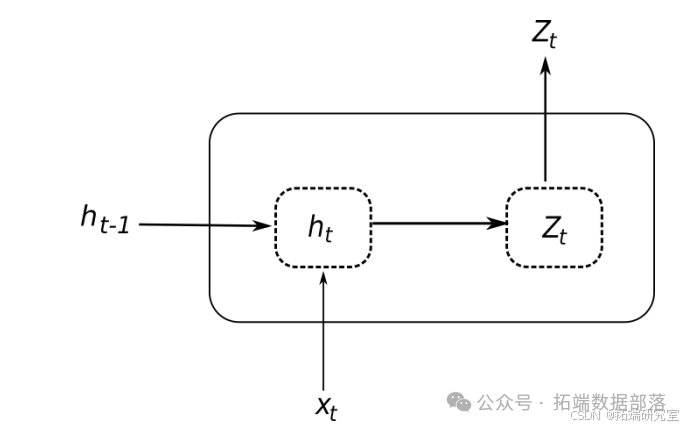
埃尔曼循环单元:基础循环单元由埃尔曼(1990)提出。基本 ERNN 单元的结构如图所示。
多年来,针对这个基础循环单元的缺点,已经引入了其他几种变体。由 Hochreiter 和 Schmidhuber(1997)提出的长短期记忆(LSTM)单元可能是自然语言处理任务中最受欢迎的单元,因为它能够在缓解梯度消失问题的同时捕获序列中的长期依赖关系。LSTM 单元的结构如图所示。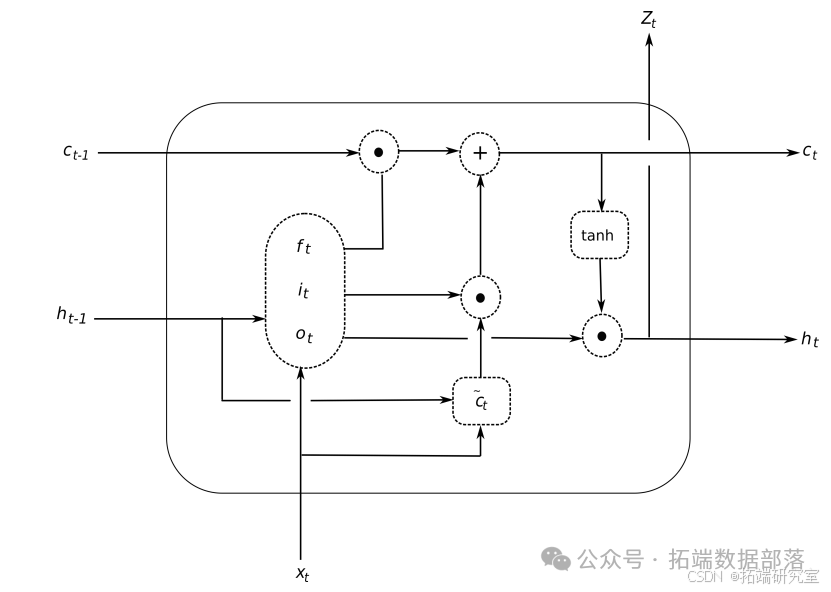
与基本 RNN 单元相比,LSTM 单元的状态有两个组件,隐藏状态和内部单元状态,其中隐藏状态对应于短期记忆组件,单元状态对应于长期记忆。凭借其内部单元状态支持的恒误差传送带(CEC)能力,LSTM 避免了梯度消失和爆炸问题。此外,还引入了一种门控机制,包括输入门、遗忘门和输出门。
堆叠架构
本研究中使用的堆叠架构与 Bandara 等人(2020)工作中提到的架构密切相关。如图所示。图 显示了 RNN 的折叠版本,而图展示了随时间展开的版本。其思想是同一 RNN 单元在每个时间步重复,它们之间共享相同的权重和偏差。单元的反馈回路帮助网络将状态 htht 传播到未来时间步。为了便于概括,图中仅显示了状态 htht;然而,对于 LSTM 单元,htht 应伴有单元状态 CtCt。
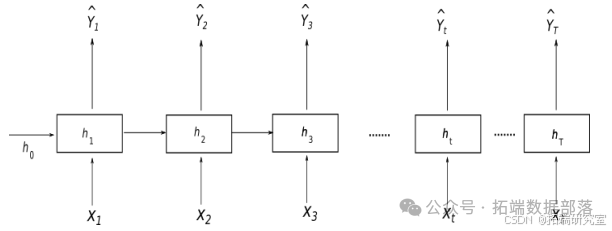
堆叠的概念意味着多个 LSTM 层可以相互堆叠。在最基本的设置中,模型只有一个 LSTM 层。
用于堆叠架构的 XtXt 和 Y^tY^t 是向量而不是单个数据点。在每个时间步,单元使用其现有权重运行并产生输出 ZtZt,该输出对应于时间序列的下一个紧邻输出窗口。同样,最后时间步的 RNN 单元实例的输出 Y^TY^T 对应于特定时间序列的预期预测。然而,单元的输出不符合预期维度,即预测范围(HH)。由于单元维度(dd)是一个外部调整的超参数,它可以取任何适当的值。因此,为了将单元的输出投影到预期的预测范围,在每个循环单元顶部连接一个仿射神经网络层,其权重与循环网络本身一起训练。这个全连接层未明确显示,输出 Y^t∈RHY^t∈RH 对应于组合的 RNN 单元和密集层的输出。
以下是可能涉及的代码示例(此处仅为示意,非完整代码):
# 构建埃尔曼循环单元模型
elman\_model = build\_elman_rnn()
# 构建堆叠架构的 RNN 模型
stacked\_model = build\_stacked_rnn()
# 训练堆叠架构模型
stacked\_model.fit(train\_data)序列到序列架构
本研究中使用的 S2S 架构如图 所示。与堆叠架构相比,S2S 网络有几个主要差异。首先是输入格式。馈入该网络每个单元实例的输入 xtxt 是单个数据点而不是向量。换句话说,该网络不使用数据预处理的移动窗口方案。RNN 单元在每个时间步不断接收输入,从而构建网络的状态。这个组件称为编码器。然而,与堆叠架构不同,不是在每个时间步考虑输出;而是仅考虑编码器最后一个输入点之后产生的预测。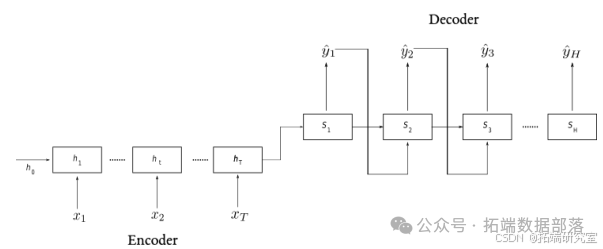
这里,每个 ytyt 对应于预测范围内的单个预测数据点。以这种方式产生输出的组件称为解码器。解码器也由一组 RNN 单元实例组成,预测范围内每个步一个。解码器的初始状态是从编码器构建的最终状态,也称为上下文向量。
在 S2S 网络中有两种基本的输出组件类型。最常见的是如上所述的解码器。受 Wen 等人(2017)工作的启发,也可以使用密集层代替解码器。我们在实验中实现了这两种可能性。然而,由于我们没有将任何未来信息馈入解码器,我们不像 Wen 等人(2017)那样使用局部 MLP 的概念,并且仅为预测范围使用一个全局 MLP。这种技术有望消除解码器中具有自回归连接的误差传播问题。
以下是可能涉及的代码示例(此处仅为示意,非完整代码):
# 构建序列到序列架构的 RNN 模型
s2s\_model = build\_s2s_rnn()
# 训练序列到序列架构模型
s2s\_model.fit(train\_data)实验框架
(一)数据集
本实验采用了多个数据集,均源自过去几年的预测竞赛,具体如下:
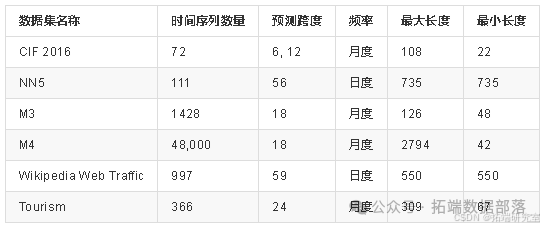
CIF 2016 预测竞赛数据集:包含 72 个月度时间序列,其中 57 个预测跨度为 12,其余 15 个为 6。部分序列为人工生成,其余来自银行领域。
NN5 预测竞赛数据集:共 111 个日度时间序列,代表英国 ATM 机近两年的每日现金提取数据,预测跨度为 56,且存在缺失值。
M3 预测竞赛数据集:2000 年举办,有 1428 个月度时间序列,预测跨度为 18,涵盖多个类别。
M4 预测竞赛数据集:2018 年举办,格式与 M3 类似,包含 100,000 个序列,仅月度子类别就有 48,000 个序列。
Wikipedia 网络流量时间序列预测竞赛数据集:任务是预测维基百科页面的未来网络流量,本研究选取前 997 篇文章在特定时期的数据,预测跨度为 59 天,数据均为整数。
旅游预测竞赛数据集:包含月度、年度和季度时间序列,本实验选用月度类别,共 366 个序列,需预测给定序列的未来 24 个月数据。
由于本研究专注于单变量、多步向前预测且仅考虑单一季节性,对于 NN5 数据集和 Wikipedia 网络流量数据集,因数据为日度且少于两年,仅考虑周季节性;从 M3 和 M4 数据集中仅使用包含单一年度季节性的月度时间序列。
各数据集的详细信息见表 :
(二)数据预处理
本研究实施了一系列预处理步骤:
数据集划分:依据 Suilin(2017)和 Bandara 等人(2020)的思路,从每个时间序列末尾预留一部分作为验证集,其长度等于预测跨度,其余部分作为训练数据。
处理缺失值:
对于 NN5 数据集,采用中位数替换法。因该数据集为日度数据,特定日期的缺失值由该周同一天的所有值的中位数替代。例如,若周二出现缺失值,则取该时间序列所有周二值的中位数作为替换值。此方法优于取所有可用数据点的中位数,因为 NN5 序列具有较强的周季节性。
for (idr in 1: nrow(nn5_dataset)) { oneLine\_df=nn5\_dataset\[idr,\] numericvalue<-as.numeric(oneLine_df) for(i in 1:length(numericvalue)){ if(i%%7==0){ sunday = append(sunday,numericvalue\[i\]) }else if(i%%7==1){ monday = append(monday,numericvalue\[i\]) }else if(i%%7==2){
对于 Kaggle 网络流量数据集,由于其缺失值较多且未区分缺失值和“0”值,对所有缺失值简单替换为“0”。
kaggle\_dataset\[is.na(kaggle\_dataset)\] = 0季节性建模:关于使用神经网络建模季节性,研究者观点不一。早期研究认为神经网络可准确建模季节性,但近期实验表明,在将数据输入神经网络之前进行去季节化处理至关重要,因为神经网络在建模季节性方面较弱。本研究核心是探究神经网络自身建模季节性的能力,因此进行了有无去除季节性的实验。若去除季节性,采用特定的去季节化程序。
稳定数据方差:若使用如 STL 分解等加法季节性分解技术,则需进行方差稳定化处理。对于时间序列预测,对数变换是一种较为直接的方差稳定方法。
多输出策略:预测问题通常是多步向前预测问题。Ben Taieb 等人(2012)对五种多步向前预测技术进行了广泛研究,包括递归策略、直接策略、DiRec 策略、多输入多输出(MIMO)策略和 DIRMO 策略。本研究中,实验表明多输出策略总体效果最佳,DIRMO 策略需谨慎选择输出窗口大小。Wen 等人(2017)也指出直接多水平策略(即 MIMO 策略)性能可靠,因其避免了预测时间步上的误差累积。
趋势归一化:RNN 单元中使用的激活函数(如 sigmoid 或双曲正切函数)存在饱和区域,输出会趋于恒定。因此,使用 RNN 单元时需确保输入充分归一化,使输出不在饱和范围内。为此,对采用移动窗口方案的 RNN 架构执行了每窗口局部归一化步骤。从每个去季节化的输入和相应的输出窗口对中,减去输入窗口最后一个时间步的趋势值(通过 STL 分解得到)。
均值归一化:对于未使用 STL 分解的实验,无法进行上述趋势归一化。在此情况下,在应用对数变换之前,对时间序列进行均值归一化。即每个时间序列除以其自身均值,这种除法而非减法有助于将所有时间序列缩放到相似范围,利于 RNN 学习过程,然后对结果数据进行对数变换。
(三)训练与验证方案
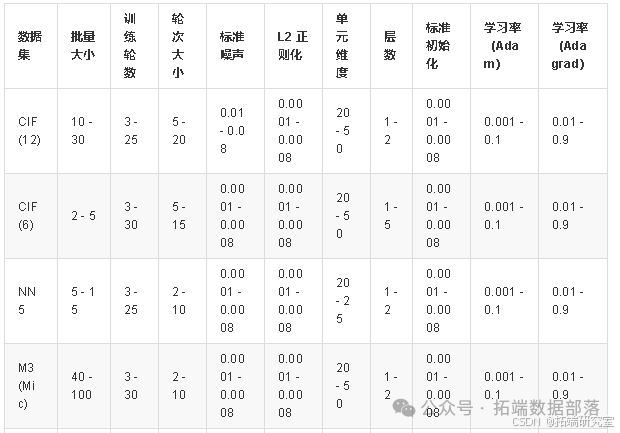
超参数调整:
实验需对多个与模型训练相关的超参数进行适当调整,包括小批量大小、训练轮数、轮次大小、学习率、高斯噪声标准差、L2 正则化参数、RNN 单元维度、隐藏层数、随机正态初始化标准差。
贝叶斯优化:上述方法逐个评估目标函数(验证误差),这意味着从头重新训练机器学习模型,计算量较大。贝叶斯优化旨在限制此类昂贵的目标函数评估次数。该技术使用高斯先验对所有可能的函数建模目标函数(Snoek 等人,2012)。此概率模型嵌入了关于待优化目标函数的所有先验假设。在每次迭代中,选择超参数空间的另一个实例来评估目标函数值。选择下一个评估点的决策取决于一个单独的采集函数的最小化/最大化,该采集函数比目标函数本身评估成本低得多。采集函数有多种形式,Snoek 等人(2012)的实现使用预期改进。采集函数的优化考虑了所有先前的目标函数评估,以确定下一个评估点。因此,与上述网格搜索和随机搜索相比,贝叶斯优化过程在函数评估方面做出更明智的决策。给定每个超参数的初始值范围和定义的迭代次数,贝叶斯优化方法使用一组先前已知的参数配置进行初始化,从而尝试为给定问题找到这些超参数的最优值。基本贝叶斯优化技术有许多实际实现和变体,如 hyperopt、spearmint 和 bayesian - optimization(Bergstra,2012;Snoek,2012;Fernando,2012)。
基于序列模型的算法配置(SMAC):SMAC 用于超参数调整,是 Hutter 等人(2011)提出的贝叶斯优化的一种变体。此实现基于基于序列模型的优化(SMBO)概念。SMBO 是一种基于贝叶斯优化思想的技术,但使用树状结构 Parzen 估计器(TPE)对目标函数建模,而非高斯先验。TPE 算法在每次迭代中为超参数生成一组候选最优值,而不像通常的贝叶斯优化仅生成一个候选值。树结构允许用户定义相互依赖的条件超参数。该过程一直进行,直到达到给定的时间限制或迭代次数。Hutter 等人(2011)的工作通过添加处理分类超参数的能力进一步增强了基本 SMBO 算法。本研究使用的 SMAC 的 Python 实现可作为 Python 包获取(Lindauer 等人,2017)。
各数据集的初始超参数范围见表 :
处理模型过拟合:机器学习模型中的过拟合是指在验证数据集上的性能远差于训练数据集上的性能。在神经网络模型中,这主要是由于大量参数导致的复杂性。为使模型更具通用性并捕捉未见过的模式,本框架采用两种技术。一种是向输入添加噪声以部分扭曲它,这里应用的噪声分布是均值为零的高斯分布,标准差作为另一个超参数处理。另一种技术是 L2 权重正则化,在损失函数中使用岭惩罚。权重正则化通过将权重纳入损失函数来避免网络权重过度增长,从而对网络增加复杂性进行惩罚。
(四)模型测试
找到最优超参数组合后,使用这些值训练模型并获得最终预测。测试时,模型使用所有可用数据进行训练,并将最终预测写入文件。为解决参数不确定性,在 10 个不同的 TensorFlow 图种子上训练所有模型,但使用相同的初始调整超参数。不重新运行超参数调整,因为这在计算上非常昂贵。不同的种子为网络提供 10 个不同的初始化。从每个模型针对不同种子获得 RNN 预测后,通过取种子间的中位数将它们组合起来。
数据后处理
为计算最终误差指标,需对生成的预测进行反向预处理操作。对于使用 STL 分解的实验,后处理步骤如下:
通过添加最后一个输入点的趋势值来反转局部归一化。
通过加回季节性成分来反转去季节化。
通过取指数来反转对数变换。
若数据包含 0,则减去 1。
对于整数数据,将预测值四舍五入到最接近的整数。
将所有负值截断为 0(使预测中仅允许正值)。
对于未使用 STL 分解的实验,预测的后处理如下:通过取指数来反转对数变换。
若数据包含 0,则减去 1。
将每个序列的预测值乘以其相应的均值以反转均值缩放的效果。
对于整数数据,将预测值四舍五入到最接近的整数。
将所有负值截断为 0(使预测中仅允许正值)。
结果分析
本实验所使用的数据集在季节性强度、时间序列数量和单个时间序列长度等方面差异较大,因此可合理假设所选数据集涵盖了足够多的不同时间序列特征,以得出一般性结论。
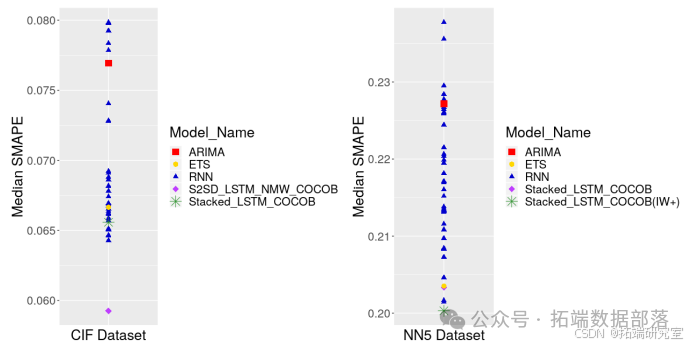
可以看出,在 CIF2016、M3、旅游和 M4 数据集上,没有模型明显优于这两个基准。在 NN5 数据集上,RNN 模型仅在性能上明显优于 auto.arima,但不优于 ets。此外,在所有数据集中,可以发现明显优于基准的 RNN 模型大多是堆叠架构的变体。并且,仅在 Wikipedia 网络流量数据集上,回归模型的合并版本明显优于基准 auto.arima。
一般而言,将滞后数量从 10 增加到 RNN 的输入窗口大小可提高所有数据集上回归模型的准确性。在 Wikipedia 网络流量、M3 和 NN5 数据集上,仅包含交叉序列信息就有效果,因为增加滞后数量的合并回归模型比未合并版本的回归模型表现更好。此外,在 Wikipedia 网络流量和 NN5 数据集上,增加滞后数量的合并回归模型优于独立作用于每个序列的 auto.arima 模型。
尽管在 CIF、旅游和 M4 数据集上合并模型的表现比未合并模型差,但 RNN 模型在这些数据集上大多优于未合并和合并回归模型。这表明,即使这些数据集中的序列不太适合构建全局模型,RNN 架构对最终准确性也有明显影响。实际上,在 CIF 数据集上,RNN 架构的选择效果优于两个统计基准 ets 和 auto.arima。在 Wikipedia 网络流量、M3 和 NN5 数据集上,RNN 也优于统计基准以及回归模型的两个版本,这意味着在这些数据集上,交叉序列的纳入以及 RNN 的选择共同导致了更好的准确性。
另一个重要观察结果是,在许多数据集上,贝叶斯优化和针对合并回归模型的 L2 正则化参数的 10 折交叉验证的超参数调整选择的值接近 0,使得模型实际上几乎没有 L2 正则化。这就是为什么在许多数据集中,有正则化和无正则化的平均 SMAPE 值相同。因此,对于合并回归模型,不能得出 L2 权重正则化可提高模型性能的结论。没有任何 L2 正则化的模型已经是数据的合适拟合。对于未合并回归模型,得到的结果好坏参半。正如 Bergmeir 等人(2018)所讨论的,虽然通用的 k 折交叉验证可用于检测过拟合,但对于欠拟合的模型可能会导致交叉验证误差的低估。然而,我们的合并回归模型没有表现出这种行为,因为它们具有非常小的 L2 正则化参数。对于未合并模型,尽管对于某些序列 L2 正则化参数较高,但 10 折交叉验证和普通交叉验证的情况相同。
(一)RNN 架构的相对性能
在所有数据集上,依据所有误差指标比较不同 RNN 架构的相对性能。图的小提琴图展示了这些结果。可以看出,最佳架构因误差指标而异。在平均 SMAPE 方面,不带移动窗口的具有密集层的序列到序列(S2SD)架构表现最佳。然而,在所有其他误差指标上,堆叠架构表现最佳。关于排名误差图,显然堆叠架构在大多数时间序列上产生最佳结果。因此,平均 SMAPE 的结果表明,堆叠架构对于某些异常时间序列会导致较高误差。S2SD 架构的两个版本(带和不带移动窗口)表现相当不错,尽管在大多数情况下不如堆叠架构。因此,在 S2SD 架构的两个版本之间,很难得出关于最佳模型的明确结论。整体而言,带解码器的 S2S 架构表现最差。
p <- ggplot(data, aes(factor(Input\_Window\_Size), Mean\_MASE\_Rank))
# p + geom\_violin() + geom\_boxplot(width=0.1, aes(fill=Input\_Window\_Size)) +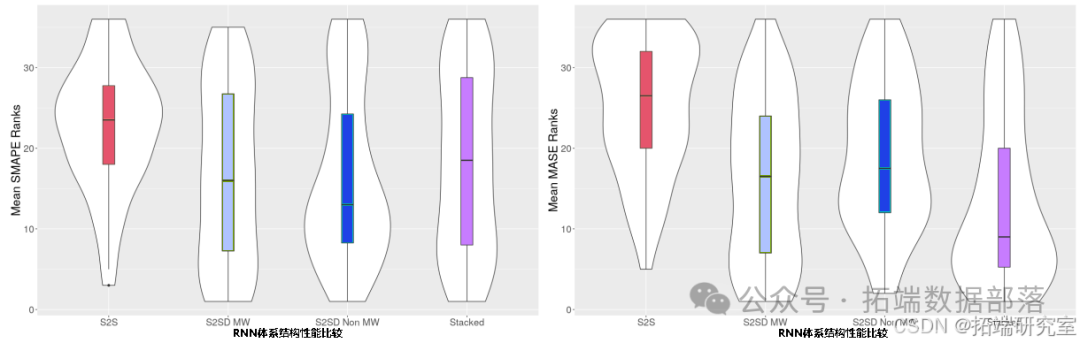
关于平均 SMAPE 值,统计显著性的 Friedman 检验给出的总体 p 值为 9.3568×10⁻³,这意味着差异具有统计学意义。使用表现最佳的 S2SD MW 架构作为对照方法进行 Hochberg 的事后检验。堆叠架构和 S2SD 非 MW 架构的表现没有明显更差,调整后的 p 值为 0.602。然而,S2S 架构的表现明显更差,调整后的 p 值为 5.24×10⁻³。在中位数 SMAPE 方面,统计显著性的 Friedman 检验给出的总体 p 值为 0.349,这意味着模型之间的差异不具有统计学意义。
点击标题查阅往期内容

【视频讲解】共享单车使用量预测:RNN, LSTM,GRU循环神经网络和传统机器学习|数据分享

左右滑动查看更多

01
02
03
04
(二)循环单元的性能
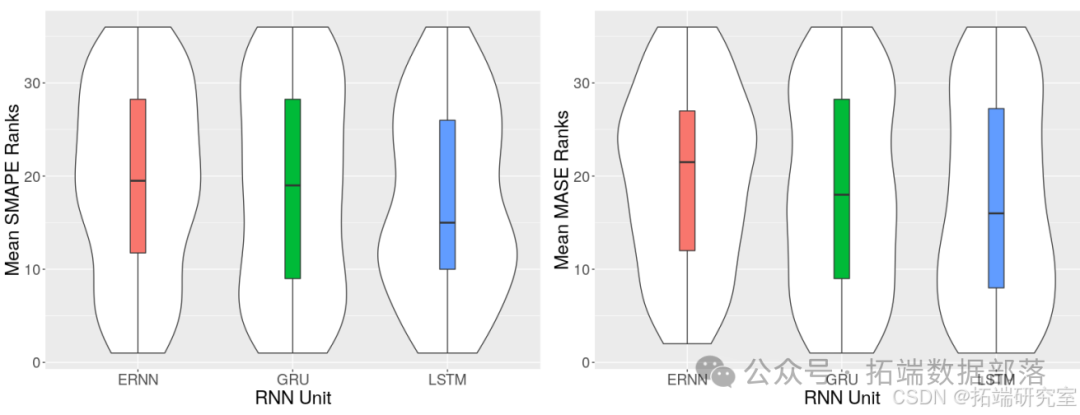
图 的小提琴图展示了不同 RNN 单元在平均 SMAPE 排名和平均 MASE 排名方面的性能比较。关于平均 SMAPE 值的统计显著性的 Friedman 检验产生的总体 p 值为 0.101。尽管 p 值未表明具有统计显著性,但从图中可以得出,具有窥视孔连接的 LSTM 单元表现最佳。ERNN 单元表现最差,GRU 的性能介于两者之间。
(三)季节性建模分析
我们还绘制了不同数据集的季节性模式,如图 所示。为便于说明,在 M4 月度数据集和 Wikipedia 网络流量数据集的每个类别中,仅绘制前 400 个序列。此外,从每个数据集的每个序列中,仅绘制前 50 个时间步。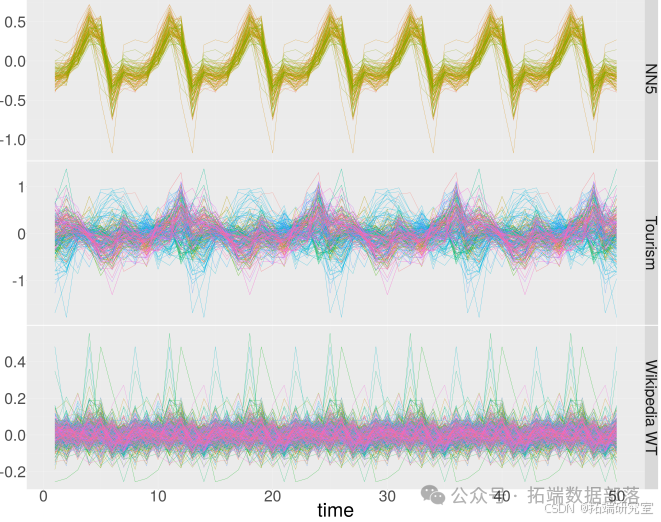
(四)RNN 模型与传统单变量基准的性能对比
模型类型在平均 SMAPE 指标和中位数 SMAPE 指标方面的相对性能分别如图 所示。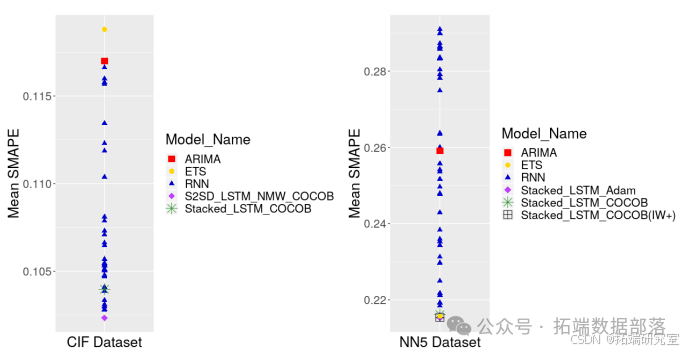
结论
本研究的动机是解决在使用 RNN 进行预测时的一些关键问题,并评估预测从业者在对这些技术了解有限的情况下如何有效地将其用于预测任务。通过对具有不同特征的数据集进行大量系统实验,我们得出了从一般数据预处理最佳实践到超参数配置、最佳 RNN 架构、循环单元和优化器等多方面的结论。所有模型都以全局模型的形式利用交叉序列信息,从而充分利用了存在大量相关时间序列的大规模时间序列数据库。
关于分析师

在此对 Pengyuan Wen 对本文所作的贡献表示诚挚感谢,他在西安电子科技大学从事统计学相关研究。擅长 R、Python,在机器学习、数据分析、数据采集等方面有着丰富的经验。

本文中分析的数据、代码分享到会员群,扫描下面二维码即可加群!

资料获取
在公众号后台回复“领资料”,可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《Python、R循环神经网络RNN、指数平滑ETS、ARIMA模型预测网络流量、ATM机取款、旅游需求时间序列数据》。
点击标题查阅往期内容
MATLAB贝叶斯优化混合Bayes-CNN-RNN分析股票市场数据与浅层网络超参数优化
R语言KERAS用RNN、双向RNNS递归神经网络、LSTM分析预测温度时间序列、 IMDB电影评分情感
Python用CNN-LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
RNN循环神经网络 、LSTM长短期记忆网络实现时间序列长期利率预测
结合新冠疫情COVID-19股票价格预测:ARIMA,KNN和神经网络时间序列分析
深度学习:Keras使用神经网络进行简单文本分类分析新闻组数据
用PyTorch机器学习神经网络分类预测银行客户流失模型
PYTHON用LSTM长短期记忆神经网络的参数优化方法预测时间序列洗发水销售数据
Python用Keras神经网络序列模型回归拟合预测、准确度检查和结果可视化
R语言深度学习卷积神经网络 (CNN)对 CIFAR 图像进行分类:训练与结果评估可视化
深度学习:Keras使用神经网络进行简单文本分类分析新闻组数据
Python用LSTM长短期记忆神经网络对不稳定降雨量时间序列进行预测分析
R语言深度学习Keras循环神经网络(RNN)模型预测多输出变量时间序列
R语言KERAS用RNN、双向RNNS递归神经网络、LSTM分析预测温度时间序列、 IMDB电影评分情感
Python用Keras神经网络序列模型回归拟合预测、准确度检查和结果可视化
Python用LSTM长短期记忆神经网络对不稳定降雨量时间序列进行预测分析
R语言中的神经网络预测时间序列:多层感知器(MLP)和极限学习机(ELM)数据分析报告
R语言深度学习:用keras神经网络回归模型预测时间序列数据
Matlab用深度学习长短期记忆(LSTM)神经网络对文本数据进行分类
R语言KERAS深度学习CNN卷积神经网络分类识别手写数字图像数据(MNIST)
MATLAB中用BP神经网络预测人体脂肪百分比数据
Python中用PyTorch机器学习神经网络分类预测银行客户流失模型
R语言实现CNN(卷积神经网络)模型进行回归数据分析
SAS使用鸢尾花(iris)数据集训练人工神经网络(ANN)模型
【视频】R语言实现CNN(卷积神经网络)模型进行回归数据分析
Python使用神经网络进行简单文本分类
R语言用神经网络改进Nelson-Siegel模型拟合收益率曲线分析
R语言基于递归神经网络RNN的温度时间序列预测
R语言神经网络模型预测车辆数量时间序列
R语言中的BP神经网络模型分析学生成绩
matlab使用长短期记忆(LSTM)神经网络对序列数据进行分类
R语言实现拟合神经网络预测和结果可视化
用R语言实现神经网络预测股票实例
使用PYTHON中KERAS的LSTM递归神经网络进行时间序列预测
python用于NLP的seq2seq模型实例:用Keras实现神经网络机器翻译
用于NLP的Python:使用Keras的多标签文本LSTM神经网络分类



![]()




















