最近看到一些模型使用了自回归方法,这里就学习一下整理一下相关内容方便以后查阅。
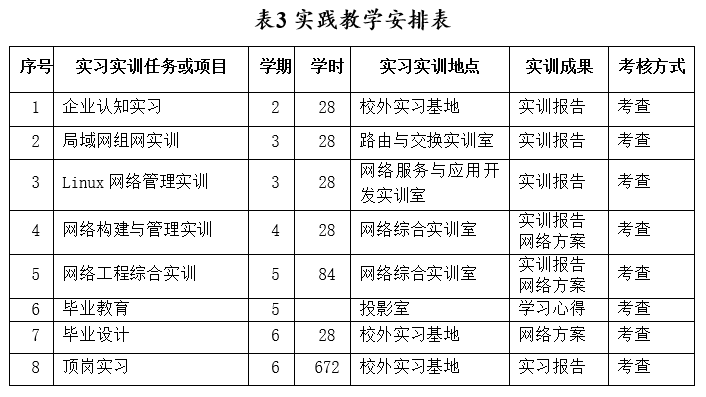
自回归模型(AR )
- 自回归模型(AR )
- AR 模型的引入
- AR 模型的定义
- 参数的估计方法
- 模型阶数选择
- 平稳性与因果性条件
- 自相关与偏自相关函数
- 优缺点总结
- 自相关(Autocorrelation)与偏自相关(Partial Autocorrelation)
- 基本概念与定义
- 自相关函数(ACF)
- 样本自相关系数
- 偏自相关函数(PACF)
- ACF与PACF图在模型识别中的作用
- 工具与代码实现
- 自回归移动平均模型(Autoregressive Moving Average Model,ARMA)
- 基本概念与定义
- 自回归(AR)模型
- 移动平均(MA)模型
- ARMA模型的定义
- ARMA(p, q)模型的数学公式
- 参考资料
自回归(Autoregression,简称AR)是一类广泛应用于时间序列分析和建模的统计模型。它的核心思想是将当前时刻的数据值表示为过去若干时刻数据值的线性组合,以及一个随机误差项。通过这种方式,自回归模型能够捕捉时间序列内部的自相关结构,从而实现对未来值的预测、对数据生成机制的理解,或对信号特征的建模。
自回归模型(AR )
AR 模型的引入
考虑如图所示的单摆系统。设
x
t
x_t
xt 为第
t
t
t 次摆动过程中的摆幅。根据物理原理,第
t
t
t 次的摆幅
x
t
x_t
xt 由前一次的摆幅
x
t
−
1
x_{t-1}
xt−1 决定,即有
x
t
=
a
1
x
t
−
1
x_t=a_1x_{t-1}
xt=a1xt−1。考虑到空气振动的影响,我们往往假设
x
t
=
a
1
x
t
−
1
+
ε
t
,
t
≥
1
x_t=a_1x_{t-1}+\varepsilon_t,t\geq1
xt=a1xt−1+εt,t≥1
其中,随机干扰 ε t ∼ N ( 0 , σ 2 ) ε_t \sim N(0, σ^2) εt∼N(0,σ2)。

设初始时刻 x 0 = 1 x_0=1 x0=1,现在取不同的 a 1 a_1 a1 和 σ σ σ 值进行实验。实验结果如下图。

可以看出,参数
a
1
a_1
a1 对序列的稳定性起到决定性的作用,而噪声强度
σ
2
σ^2
σ2 决定了序列的波动程度。
在这里,我们称第一个公式为一阶自回归模型。更一般地,可以考虑序列值
x
t
x_t
xt 可由前
p
p
p 个时刻的序列值及当前的噪声表出,即
x
t
=
a
1
x
t
−
1
+
a
2
x
t
−
2
+
⋯
+
a
p
x
t
−
p
+
ε
t
x_t=a_1x_{t-1}+a_2x_{t-2}+\cdots+a_px_{t-p}+\varepsilon_t
xt=a1xt−1+a2xt−2+⋯+apxt−p+εt
其中, a j a_j aj 为参数, ε t {ε_t} εt 为白噪声。
AR 模型的定义
如果
ε
t
\varepsilon_\mathrm{t}
εt为白噪声,服从
N
(
0
,
σ
2
)
N(0,\sigma^2)
N(0,σ2),
a
0
,
a
1
,
.
.
.
,
a
p
(
a
p
≠
o
)
\mathrm{a_0,a_1,...,a_p(a_p\neq o)}
a0,a1,...,ap(ap=o)为实数,就称
p
p
p 阶差分方程
X
t
=
a
0
+
a
1
X
t
−
1
+
a
2
X
t
−
2
+
⋯
+
a
p
X
t
−
p
+
ε
t
,
t
∈
Z
X_t=a_0+a_1X_{t-1}+a_2X_{t-2}+\cdots+a_pX_{t-p}+\varepsilon_t,t\in\mathbb{Z}
Xt=a0+a1Xt−1+a2Xt−2+⋯+apXt−p+εt,t∈Z
是一个 p p p 阶自回归模型,简称 A R ( p ) AR(p) AR(p) 模型,称 a = ( a 0 , a 1 , . . . , a p ) T \mathbf{a=(a_{0},a_{1},...,a_{p})^{T}} a=(a0,a1,...,ap)T是 A R ( p ) AR(p) AR(p) 模型中的自回归系数。满足上述 模型的时间序列 X t {X_t} Xt 称为 A R ( p ) AR(p) AR(p) 序列。
当
a
0
=
0
a_0=0
a0=0 时,称为零均值
A
R
(
p
)
AR(p)
AR(p) 序列,即
X
t
=
a
1
X
t
−
1
+
a
2
X
t
−
2
+
⋯
+
a
p
X
t
−
p
+
ε
t
,
t
∈
Z
X_t=a_1X_{t-1}+a_2X_{t-2}+\cdots+a_pX_{t-p}+\varepsilon_t,t\in\mathbb{Z}
Xt=a1Xt−1+a2Xt−2+⋯+apXt−p+εt,t∈Z
需要指出的是,对于 a 0 ≠ 0 a_0≠0 a0=0 的情况,我们可以通过零均值化的手段把一般的 A R ( p ) AR(p) AR(p) 序列变为零均值 A R ( p ) AR(p) AR(p) 序列。
参数的估计方法
要使用AR模型进行预测或分析,我们需要根据实际数据估计参数 ϕ 1 , ϕ 2 , … , ϕ p \phi_1, \phi_2, \dots, \phi_p ϕ1,ϕ2,…,ϕp 和噪声项的方差 σ 2 \sigma^2 σ2。参数估计方法包括:
-
最小二乘法(OLS):将 AR 模型视为线性回归模型,用 OLS 来估计参数。对于 AR§ 模型,可将 ( x t − 1 , x t − 2 , … , x t − p ) (x_{t-1}, x_{t-2}, \dots, x_{t-p}) (xt−1,xt−2,…,xt−p) 作为自变量, x t x_t xt 为因变量,构建线性方程组,求解参数。
-
极大似然估计(MLE):在高斯噪声假设下,可采用MLE方法,通过最大化似然函数来得到参数估计。
-
Yule-Walker方程:Yule-Walker方程是基于自相关函数推导出的方程组,可以直接求解AR模型参数。这在理论研究和快速估计中非常有用。
模型阶数选择
确定 AR 模型的阶数 p p p 是实际应用中的一个关键步骤。过低的阶数可能无法充分捕捉序列的特征,过高的阶数又会导致过拟合和模型复杂度增加。常用的阶数选择标准包括:
-
赤池信息准则(AIC): AIC = 2 k − 2 ln ( L ) \text{AIC} = 2k - 2\ln(L) AIC=2k−2ln(L),其中 k k k 是参数个数, L L L 为似然函数值。AIC倾向较复杂模型,但不宜过于简单。
-
贝叶斯信息准则(BIC): BIC = ln ( N ) k − 2 ln ( L ) \text{BIC} = \ln(N)k - 2\ln(L) BIC=ln(N)k−2ln(L),其中 N N N 为样本量。BIC惩罚项更大,倾向更简单的模型。
-
HQ准则(Hannan-Quinn):介于 AIC 和 BIC 之间的准则。
一般来说,通过对不同阶数的模型拟合并计算AIC、BIC、HQ等指标,选择使这些准则达到最低值的阶数作为最终模型的阶数。
平稳性与因果性条件
AR模型适用于平稳时间序列,因此研究 AR 模型时需要确保模型的平稳性。一个
A
R
(
p
)
AR(p)
AR(p) 模型的平稳性条件可以通过其特征方程来判断:
1
−
ϕ
1
z
−
ϕ
2
z
2
−
⋯
−
ϕ
p
z
p
=
0.
1 - \phi_1 z - \phi_2 z^2 - \cdots - \phi_p z^p = 0.
1−ϕ1z−ϕ2z2−⋯−ϕpzp=0.
如果该特征方程的根都落在单位圆之外(即绝对值大于1),那么该 A R ( p ) AR(p) AR(p) 模型是平稳的。平稳性保证了模型参数的统计性质和预测稳定性。如果时间序列不平稳,可对数据进行差分、去趋势或其他平稳化处理后再建模(这类模型可扩展为ARIMA模型)。
自相关与偏自相关函数
AR模型参数与时间序列的自相关特性密切相关。通过自相关函数(ACF)和偏自相关函数(PACF),我们可以获得有助于选择AR阶数的信息。
对于 A R ( p ) AR(p) AR(p) 模型,偏自相关函数在滞后阶数 p p p 处通常会出现截断,这为阶数选择提供了直观的参考。
优缺点总结
优点:
- 模型简单易懂,参数有明确的统计学含义。
- 算法成熟,估计方法(OLS、MLE、Yule-Walker)简单且高效。
- 对短期预测十分有效,在数据平稳且线性特征显著时表现良好。
缺点:
- 不适用于非线性序列,需要扩展方法或非线性模型来处理。
- 对非平稳序列需预处理,否则无法保证参数估计的有效性。
- 长期预测不如短期预测准确,对突发性、非线性、复杂行为的序列无能为力。
自相关(Autocorrelation)与偏自相关(Partial Autocorrelation)
自相关(Autocorrelation)与偏自相关(Partial Autocorrelation)是时间序列分析中的两个重要统计工具,用于刻画序列中不同时间点之间的相关关系结构。通过自相关和偏自相关函数(分别记为ACF与PACF),我们可以更清晰地了解序列的动态特性,并为模型阶数选择(如AR模型中的阶数 p p p)提供依据。
基本概念与定义
自相关函数(ACF)
自相关描述同一时间序列在不同时间滞后(lag)下的相关程度。对于一个离散时间序列 { x t } \{x_t\} {xt},其均值为 μ \mu μ,自相关可以定义为同一序列在时间间隔为 k k k (又称滞后数)的两个值之间的线性相关程度。
形式化定义:
设
γ
(
k
)
\gamma(k)
γ(k) 为时间序列在滞后数为
k
k
k 时的协方差,
γ
(
0
)
\gamma(0)
γ(0) 为序列的方差,则自相关函数(Autocorrelation Function, ACF)为:
ρ
(
k
)
=
γ
(
k
)
γ
(
0
)
=
E
[
(
x
t
−
μ
)
(
x
t
−
k
−
μ
)
]
E
[
(
x
t
−
μ
)
2
]
.
\rho(k) = \frac{\gamma(k)}{\gamma(0)} = \frac{E[(x_t - \mu)(x_{t-k} - \mu)]}{E[(x_t-\mu)^2]}.
ρ(k)=γ(0)γ(k)=E[(xt−μ)2]E[(xt−μ)(xt−k−μ)].
其中:
- ρ ( k ) \rho(k) ρ(k) 为滞后 k k k 的自相关系数,取值范围为[-1, 1]。
- 当 ρ ( k ) \rho(k) ρ(k) 接近1或-1时,表示序列在滞后 k k k 处具有较强的正相关或负相关。
- 当 ρ ( k ) \rho(k) ρ(k) 接近0时,表示在滞后 k k k 处序列的值与过去的值几乎没有线性关系。
通过计算序列在不同滞后下的自相关,可以构建一组自相关系数,并将其作为自相关函数ACF对滞后数k绘制得到ACF图。
样本自相关系数
在实际应用中,由于未知总体参数,我们通常使用样本自相关系数来估计ACF:
ρ
^
(
k
)
=
∑
t
=
k
+
1
N
(
x
t
−
x
ˉ
)
(
x
t
−
k
−
x
ˉ
)
∑
t
=
1
N
(
x
t
−
x
ˉ
)
2
\hat{\rho}(k)=\frac{\sum_{t=k+1}^N(x_t-\bar{x})(x_{t-k}-\bar{x})}{\sum_{t=1}^N(x_t-\bar{x})^2}
ρ^(k)=∑t=1N(xt−xˉ)2∑t=k+1N(xt−xˉ)(xt−k−xˉ)
x ‾ \overline{x} x是样本均值, N N N 是样本大小。
偏自相关函数(PACF)
偏自相关(Partial Autocorrelation)描述的是在考虑中间滞后项的影响后,两个时间点之间的“净”相关度。
偏自相关函数衡量的是在控制了中间所有滞后项的影响后,时间序列在滞后k处的直接相关性。也就是说,PACF
α
(
k
)
α(k)
α(k) 是在考虑了滞后1到滞后
k
−
1
k−1
k−1的影响后,
x
t
x_t
xt 与
x
t
−
k
x_{t−k}
xt−k 之间的净相关性。
x
t
=
β
0
+
β
1
x
t
−
1
+
β
2
x
t
−
2
+
⋯
+
β
k
x
t
−
k
+
ϵ
t
x_t=\beta_0+\beta_1x_{t-1}+\beta_2x_{t-2}+\cdots+\beta_kx_{t-k}+\epsilon_t
xt=β0+β1xt−1+β2xt−2+⋯+βkxt−k+ϵt
偏自相关函数 α ( k ) \alpha(k) α(k) 就是回归系数 β k \beta_{k} βk。
ACF与PACF图在模型识别中的作用
在AR模型中,ACF与PACF图是选择模型阶数的重要视觉和理论依据。
-
纯AR模型中的特征:
对于一个 A R ( p ) AR(p) AR(p) 模型:
x t = ϕ 1 x t − 1 + ϕ 2 x t − 2 + ⋯ + ϕ p x t − p + ϵ t , x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t, xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵt,- ACF图通常会表现为在前几个滞后可能较大(可能逐渐衰减)的自相关,然后在高阶滞后趋近于0。
- PACF图对于 A R ( p ) AR(p) AR(p)模型有一个明显特征:从滞后p之后,偏自相关系数会快速趋近于0,而且在p阶截断。也就是说,偏自相关函数在滞后数超过p时通常不显著。
-
纯MA模型中的特征:
若是一个 M A ( q ) MA(q) MA(q) 模型(非AR结构),则ACF在q阶后截断(即ACF在滞后q后接近0),而PACF表现为渐进衰减,不会像AR模型那样干净地截断。 -
ARMA模型中的特征:
对于混合模型 A R M A ( p , q ) ARMA(p,q) ARMA(p,q),ACF和PACF都不会出现干净的截断,而是呈现混合的渐进衰减特性。透过ACF和PACF的形态,可以尝试区分AR、MA及ARMA等模型结构。
通过观察ACF和PACF的截断与衰减模式,我们能够初步推断合适的模型类别与阶数。例如:
- 如果PACF在p阶截断,而ACF渐进衰减,那么这可能是AR§模型。
- 如果ACF在q阶截断,而PACF渐进衰减,那么这可能是MA(q)模型。
- 如果两者都渐进衰减,那么可能是ARMA模型,需要更进一步检验。
工具与代码实现
- 导入库并加载数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima_process import ArmaProcess
# 生成AR(1)模型的数据
np.random.seed(42)
phi = 0.6
ar = np.array([1, -phi]) # 注意符号
ma = np.array([1]) # MA部分
arma_process = ArmaProcess(ar, ma)
simulated_data = arma_process.generate_sample(nsample=100)
- 绘制ACF和PACF图
fig, ax = plt.subplots(2, 1, figsize=(12,8))
# 绘制ACF图
plot_acf(simulated_data, lags=20, ax=ax[0])
ax[0].set_title('Autocorrelation Function (ACF)')
# 绘制PACF图
plot_pacf(simulated_data, lags=20, ax=ax[1], method='ywm')
ax[1].set_title('Partial Autocorrelation Function (PACF)')
plt.tight_layout()
plt.show()

自回归移动平均模型(Autoregressive Moving Average Model,ARMA)
自回归移动平均模型(Autoregressive Moving Average Model,简称ARMA) 是时间序列分析中一种经典且广泛应用的统计模型。它结合了**自回归(Autoregressive, AR)和移动平均(Moving Average, MA)**两种模型的特点,用于描述和预测平稳时间序列数据。ARMA模型在经济学、金融学、气象学、工程学等多个领域都有着重要的应用。
基本概念与定义
自回归(AR)模型
自回归(Autoregressive, AR)模型 假设当前时间点的值是其前若干时间点值的线性组合,加上一个白噪声误差项。AR模型用于捕捉时间序列中的自相关性。
AR§模型 的数学表达式为:
x
t
=
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
⋯
+
ϕ
p
x
t
−
p
+
ϵ
t
x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t
xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵt
其中:
- x t x_t xt 是时间序列在时刻 t t t 的值。
- ϕ 1 , ϕ 2 , … , ϕ p \phi_1, \phi_2, \dots, \phi_p ϕ1,ϕ2,…,ϕp 是自回归系数。
- ϵ t \epsilon_t ϵt 是白噪声误差项,满足 E [ ϵ t ] = 0 E[\epsilon_t] = 0 E[ϵt]=0 和 Var ( ϵ t ) = σ 2 \text{Var}(\epsilon_t) = \sigma^2 Var(ϵt)=σ2。
移动平均(MA)模型
移动平均(Moving Average, MA)模型 假设当前时间点的值是前若干时间点误差项的线性组合,加上一个当前的白噪声误差项。MA模型用于捕捉时间序列中的随机波动。
MA(q)模型 的数学表达式为:
x
t
=
ϵ
t
+
θ
1
ϵ
t
−
1
+
θ
2
ϵ
t
−
2
+
⋯
+
θ
q
ϵ
t
−
q
x_t = \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}
xt=ϵt+θ1ϵt−1+θ2ϵt−2+⋯+θqϵt−q
其中:
- x t x_t xt 是时间序列在时刻 t t t 的值。
- θ 1 , θ 2 , … , θ q \theta_1, \theta_2, \dots, \theta_q θ1,θ2,…,θq 是移动平均系数。
- ϵ t \epsilon_t ϵt 是白噪声误差项,满足 E [ ϵ t ] = 0 E[\epsilon_t] = 0 E[ϵt]=0 和 Var ( ϵ t ) = σ 2 \text{Var}(\epsilon_t) = \sigma^2 Var(ϵt)=σ2。
ARMA模型的定义
自回归移动平均(Autoregressive Moving Average, ARMA)模型 结合了AR和MA模型的特点,用于描述具有自回归和移动平均特征的时间序列数据。
ARMA(p, q)模型 的数学表达式为:
x
t
=
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
⋯
+
ϕ
p
x
t
−
p
+
ϵ
t
+
θ
1
ϵ
t
−
1
+
θ
2
ϵ
t
−
2
+
⋯
+
θ
q
ϵ
t
−
q
x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}
xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵt+θ1ϵt−1+θ2ϵt−2+⋯+θqϵt−q
其中:
- p p p 是自回归部分的阶数。
- q q q 是移动平均部分的阶数。
- ϕ i \phi_i ϕi 和 θ j \theta_j θj 分别是AR和MA部分的系数。
- ϵ t \epsilon_t ϵt 是白噪声误差项。
ARMA模型 适用于平稳时间序列数据,能够捕捉序列中的长期依赖性(通过AR部分)和短期波动性(通过MA部分)。
ARMA(p, q)模型的数学公式
综合AR和MA模型,ARMA(p, q) 模型的数学公式如下:
x
t
=
ϕ
1
x
t
−
1
+
ϕ
2
x
t
−
2
+
⋯
+
ϕ
p
x
t
−
p
+
ϵ
t
+
θ
1
ϵ
t
−
1
+
θ
2
ϵ
t
−
2
+
⋯
+
θ
q
ϵ
t
−
q
x_t = \phi_1 x_{t-1} + \phi_2 x_{t-2} + \cdots + \phi_p x_{t-p} + \epsilon_t + \theta_1 \epsilon_{t-1} + \theta_2 \epsilon_{t-2} + \cdots + \theta_q \epsilon_{t-q}
xt=ϕ1xt−1+ϕ2xt−2+⋯+ϕpxt−p+ϵt+θ1ϵt−1+θ2ϵt−2+⋯+θqϵt−q
可以将其表示为:
ϕ
(
B
)
x
t
=
θ
(
B
)
ϵ
t
\phi(B) x_t = \theta(B) \epsilon_t
ϕ(B)xt=θ(B)ϵt
其中:
- ϕ ( B ) = 1 − ϕ 1 B − ϕ 2 B 2 − ⋯ − ϕ p B p \phi(B) = 1 - \phi_1 B - \phi_2 B^2 - \cdots - \phi_p B^p ϕ(B)=1−ϕ1B−ϕ2B2−⋯−ϕpBp 是AR多项式。
- θ ( B ) = 1 + θ 1 B + θ 2 B 2 + ⋯ + θ q B q \theta(B) = 1 + \theta_1 B + \theta_2 B^2 + \cdots + \theta_q B^q θ(B)=1+θ1B+θ2B2+⋯+θqBq 是MA多项式。
- B B B 是滞后算子, B x t = x t − 1 B x_t = x_{t-1} Bxt=xt−1。
参考资料
自回归模型(AR )



![2024.11.29——[HCTF 2018]WarmUp 1](https://i-blog.csdnimg.cn/direct/cd767827437f4bc1a2cddc86980b47da.png)