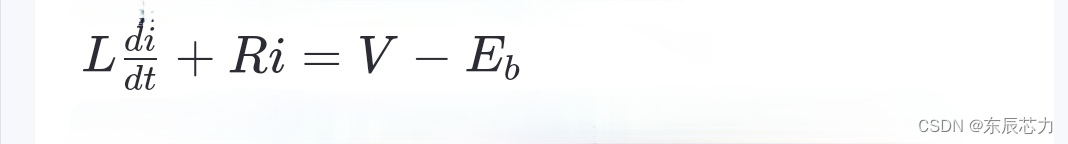引言

学习递归算法的时候，找到了用来计算算法复杂度的主定理。问大语言模型，发现回答的主定理描述有所不同。本文比较了两个不同版本中表述的差异。并给出一些例子用来计算分治递归类算法的复杂度。

主定理的不同版本

版本1

在《算法导论》第三版第四章中，主定理的定义如下：

主定理适用于求解如下递归式算法的时间复杂度：

$T(n)=aT\left(\frac{n}{b}\right)+f(n)$

其中：

• ( n ) 是问题规模大小；
• ( a ) 是原问题的子问题个数；
• $(\frac{n}{b})$ 是每个子问题的大小，这里假设每个子问题有相同的规模大小；
• ( f(n) ) 是将原问题分解成子问题和将子问题的解合并成原问题的解的时间。

对于上述递归式，主定理提供了三种情况来确定时间复杂度 $T(n)$：

1. 若$(f(n)=O(n^{{\log }_{b}a-ϵ}))，(ϵ>0)$则 $(T(n)=\Theta (n^{{\log }_{b}a}))$；
2. 若 $f(n)=\Theta (n^{{\log }_{b}a})$，则 $(T(n)=\Theta (n^{{\log }_{b}a}\log n))$；
3. 若$f(n)=\Omega (n^{{\log }_{b}a+ϵ})，ϵ>0$，且对于某个常数 $c<1$ 和所有充分大的 n 有 $af\left(\frac{n}{b}\right)\le cf(n)$，则 $T(n)=\Theta (f(n))$。

版本2

问AI大模型ChatGLM有时候会给出以下回答：
主定理适用于形式如下的递归关系：

$$T(n)=aT\left(\frac{n}{b}\right)+f(n)$$

其中：

• $T(n)$ 是算法的时间复杂度函数。
• $a\ge 1$ 是每次递归调用分解出的子问题的数量。
• $b>1$ 是每次递归调用时问题规模的缩小比例。
• $f(n)$ 是除了递归调用外，算法在每层递归中所做的其他工作。

主定理根据 $f(n)$ 和 $n^{{\log }_{b}a}$ 的关系，提供了三种情况来确定 $T(n)$ 的时间复杂度：

1. 情况1： 如果 $f(n)=O(n^{{\log }_{b}a-ϵ})$ 对于某个常数 $ϵ>0$ 成立，则 $T(n)=\Theta (n^{{\log }_{b}a})$。

2. 情况2： 如果 $f(n)=\Theta (n^{{\log }_{b}a}{\log }^{k}n)$ 对于某个常数 $k\ge 0$ 成立，则 $T(n)=\Theta (n^{{\log }_{b}a}{\log }^{k+1}n)$。

3. 情况3： 如果 $f(n)=\Omega (n^{{\log }_{b}a+ϵ})$ 对于某个常数 $ϵ>0$ 成立，并且如果 $af\left(\frac{n}{b}\right)\le cf(n)$ 对于某个常数 $c<1$ 和所有足够大的 $n$ 成立，则 $T(n)=\Theta (f(n))$。

比较这两个版本，只有情况2有所变化。版本2中f(n)可以是线性对数。而版本1中f(n)只能是多项式。所以第二个版本拓展了对数这种情况。

翻到《算法导论》第三版中的例题，给出了该拓展情况：

主定理的应用

1.大数乘法

Karatsuba乘法是一种快速乘法算法，由苏联数学家Anatoliy Karatsuba在1960年提出，并在1962年发表。这种算法通过递归地将大数分解为较小的数，然后进行乘法运算，减少了所需的乘法次数，从而提高了大数乘法的效率。

Karatsuba乘法的基本步骤如下：

1. 数字分解：将两个大数 $x$ 和 $y$ 分解为两部分，每部分大约是原数的一半。如果 $x$ 和 $y$ 都是 $n$ 位数字，则可以写为：
   $x=x_1\cdot 10^m+x_0$
   $y=y_1\cdot 10^m+y_0$
   其中 $m$ 是一个正整数，$m<n$，且 $ x_0 $ 和 $y_0$ 小于 $10^m$。

2. 递归乘法：通过递归地应用Karatsuba算法，计算以下三个乘积：

   • $z_2=x_1\cdot y_1$
   • $z_0=x_0\cdot y_0$
   • $z_1=(x_1+x_0)\cdot (y_1+y_0)-z_2-z_0$

3. 结果合并：最后，将这三个乘积合并以得到最终结果：
   $xy=z_2\cdot 10^{2m}+z_1\cdot 10^m+z_0$

复杂度分析：

大数相乘的递归表达式

$T(n)=\{\begin{array}{ll}O(1)& \text{if }n=1\\ 3T(n/2)+O(n)& \text{if }n>1\end{array}$

• 传统乘法的复杂度是 $O(n^2)$，而Karatsuba算法的复杂度仅为 $O(n^{{\log }_{2}3})$，大约是 $O(n^{1.585})$。

Python实现示例：

from math import ceil

def karatsuba(x, y):
    if x < 10 or y < 10:  # 基本情况，当x和y为个位数时
        return x * y
    n = max(len(str(x)), len(str(y)))
    m = ceil(n / 2)  # m是n的一半，向上取整
    x_H = x // (10 ** m)  # x的高半部分
    x_L = x % (10 ** m)  # x的低半部分
    y_H = y // (10 ** m)  # y的高半部分
    y_L = y % (10 ** m)  # y的低半部分
    a = karatsuba(x_H, y_H)  # 计算高半部分的乘积
    d = karatsuba(x_L, y_L)  # 计算低半部分的乘积
    e = karatsuba(x_H + x_L, y_H + y_L) - a - d  # 计算中间部分的乘积
    return int(a * (10 ** (2 * m)) + e * (10 ** m) + d)  # 合并结果

# 测试Karatsuba乘法
print(karatsuba(1234, 4321))

这种算法通过减少乘法的次数，显著提高了大数乘法的效率，尤其是在处理非常大的数字时。一般化以后有Toom-Cook乘法。

2.strassen矩阵相乘

Strassen算法是一种高效的矩阵乘法算法，由德国数学家Volker Strassen在1969年提出。它通过减少所需的乘法次数来提高矩阵乘法的效率。传统的矩阵乘法对于两个n×n的矩阵需要$n^3$次乘法，而Strassen算法只需要大约$n^{2.81}$次乘法，这在大矩阵乘法中可以显著减少计算量。

Strassen算法的核心思想是将两个2×2矩阵的乘法分解为更小的子矩阵乘法，而不是直接计算四个乘积。对于两个2×2矩阵A和B，传统的乘法需要8次乘法，而Strassen算法只需要7次乘法，如下所示：

设矩阵A和B为：
$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right],B=\left[\begin{array}{cc}e& f\\ g& h\end{array}\right]$

传统的乘法结果矩阵C为：
$C=AB=\left[\begin{array}{cc}ae+bg& af+bh\\ ce+dg& cf+dh\end{array}\right]$

Strassen算法通过以下步骤计算C：

1. 计算七个乘积：
   $M_1=(a+d)(e+h)$
   $M_2=(b+d)h$
   $M_3=a(f-h)$
   $M_4=d(g-e)$
   $M_5=(a+b)e$
   $M_6=(c+d)(f+h)$
   $M_7=(a-c)(e+f)$

2. 然后计算结果矩阵C的四个元素：
   $C_{11}=M_1+M_4-M_5+M_7$
   $C_{12}=M_3+M_5$
   $C_{21}=M_2+M_4$
   $C_{22}=M_1-M_2+M_3+M_6$

对于更大的矩阵，Strassen算法可以递归地应用到子矩阵上。这种方法可以减少乘法的次数，但是会增加加法和减法的次数。尽管如此，对于大规模的矩阵乘法，Strassen算法仍然可以提供显著的性能提升。

需要注意的是，Strassen算法的常数因子较大，因此在小规模矩阵上可能不如传统算法快。但是，随着矩阵规模的增加，其优势会逐渐显现。

递推表达式：
$T(n)=7T\left(\frac{n}{2}\right)+\Theta (n^2)$

主定理（Master Theorem）是用于确定分治算法时间复杂度的一个工具。它适用于形如下列形式的递归关系：

$T(n)=aT\left(\frac{n}{b}\right)+f(n)$

其中 $a\ge 1$，$b>1$，且 $f(n)$ 是一个渐进正函数。主定理提供了一种直接的方法来确定 $T(n)$ 的渐进上界，而不需要展开递归。

对于Strassen矩阵乘法，我们有递归关系：

$T(n)=7T\left(\frac{n}{2}\right)+\Theta (n^2)$

带入到主定理中这里，$a=7$，$b=2$，$f(n)=\Theta (n^2)$。

• ${\log }_{b}a={\log }_{2}7$，这大约是 2.807。
• $f(n)=\Theta (n^2)$。

$f(n)=n^2$ ，因为 $2<{\log }_{2}7$。这意味着 $f(n)$ 落在主定理的第三种情况

因此，根据主定理的第三种情况，我们得到：

$T(n)=\Theta (n^{{\log }_{b}a})=\Theta (n^{{\log }_{2}7})$