PyTorch使用教程-深度学习框架

1. PyTorch简介

1.1-什么是PyTorch

​ PyTorch是一个广泛使用的开源机器学习框架，特别适合深度学习的应用。它以其动态计算图而闻名，允许在运行时修改模型，使得实验和调试更加灵活。PyTorch提供了强大的GPU加速功能，支持自动微分，简化了梯度计算和模型训练。此外，PyTorch拥有直观的API，与Python深度集成，使得它易于学习和使用。它还拥有一个庞大的社区和丰富的生态系统，包括预训练模型和专用库，适用于计算机视觉、自然语言处理等多种任务。PyTorch的灵活性和强大的功能使其成为研究人员和开发者的首选工具之一。

1.2-为什么要使用PyTorch

1. 动态计算图：PyTorch的动态计算图使得模型构建更加灵活，可以在运行时更改模型结构，适合研究和原型设计。
2. 易用性和灵活性：PyTorch的API设计直观，与Python深度集成，使得学习和使用变得简单愉快。
3. 易于调试：由于PyTorch的动态性和Python性质，使用标准Python调试工具可以方便地调试程序。
4. 强大的社区支持：PyTorch拥有一个活跃的社区，用户可以在官方论坛、GitHub、Stack Overflow等平台上找到大量资源和帮助。
5. 广泛的预训练模型：PyTorch提供了大量的预训练模型，如ResNet、VGG、Inception等，这些模型可以帮助用户快速开始新项目。
6. 高效的GPU利用：PyTorch可以高效地利用NVIDIA的CUDA库进行GPU计算，并支持分布式计算，允许在多个GPU或服务器上训练模型。

1.3-PyTorch核心组件

• 张量（Tensor）

​ 在PyTorch中，张量是数据的基本表示形式，可以有任意数量的维度，这使得它们非常灵活。PyTorch的张量数据类型，类似于多维数组，用于存储和操作模型的输入和输出以及模型的参数。张量与NumPy的 ndarray 类似，只是张量可以在 GPU 上运行以加速计算。在 PyTorch 中，张量以 “类” 的形式封装起来，对张量的一些运算、处理的方法被封装在类中

1. 标量（0阶张量）：标量是一个单一的数值
2. 向量（1阶张量）：向量是一维数组，可以表示为一列或一行数值
3. 矩阵（2阶张量）：矩阵是一个二维数组，包含行和列
4. 高阶张量：高阶张量是更高维度的数组。

• 图形

​ 图形是由已连接节点（称为顶点）和边缘组成的数据结构。每个现代深度学习框架都基于图形的概念，其中神经网络表示为计算的图形结构。PyTorch 在由函数对象组成的有向无环图 (DAG) 中保存张量和执行操作的记录。

1.4-PyTorch安装

# 直接安装
pip install torch

# 使用代理镜像源
pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple

# 指定版本安装
pip install torch==2.3.1 -i https://pypi.tuna.tsinghua.edu.cn/simple

建议python使用版本不要太老，否则安装torch相对早些版本

2. PyTorch使用

创建一个test01.py，进行代码的调试使用

#!/usr/bin/env python3
# -*- coding:utf-8 -*-
# @Project  :hello-algo-main
# @File     :test01.py
# @Time     :2024/11/11 23:15

import torch
import numpy as np

2.1. 张量的创建

2.1.1-torch.tensor()

根据指定数据创建张量

• 标量

# 创建张量 - 标量
data1 = torch.tensor(666)
print(data1)
print(type(data1))
print(data1.shape)

"""
输出：
tensor(666)
<class 'torch.Tensor'>
torch.Size([])
"""

• 使用torch.tensor(666)创建了一个标量张量data1，其值为666。
• 打印出data1的内容、类型和形状。类型为torch.Tensor 类，形状为torch.Size([])，表示这是一个0维张量（标量）。

• numpy 数组

# numpy 数组
data2 = torch.tensor(np.random.randn(2, 4))
print(data2)
print(type(data2))
print(data2.shape)
"""
输出：
tensor([[-0.1815,  0.4556, -0.6612, -0.7966],
        [-0.9630,  0.4847,  0.2520, -0.2234]], dtype=torch.float64)
<class 'torch.Tensor'>
torch.Size([2, 4])
"""

• 使用np.random.randn(2, 4)生成一个2x4的两行四列NumPy数组，并用torch.tensor()将其转换为PyTorch张量data2。
• 打印出data2的内容、类型和形状。类型为torch.Tensor 类，形状为torch.Size([2, 4])，表示这是一个2维张量（矩阵）。

• 列表

# 列表
data3 = [[1, 2, 3], [4, 5, 6]]
data3_t = torch.tensor(data3)
print(data3_t)
print(type(data3_t))
print(data3_t.shape)
"""
输出：
tensor([[1, 2, 3],
        [4, 5, 6]])
<class 'torch.Tensor'>
torch.Size([2, 3])
"""

• 定义一个Python列表data3，并使用torch.tensor()将其转换为PyTorch张量data3_t。
• 打印出data3_t的内容、类型和形状。类型为torch.Tensor 类，形状为torch.Size([2, 3])，表示这是一个2维张量。

2.1.2-torch.Tensor()

根据指定形状创建张量，也可以用来创建指定数据的张量

# 创建2行3列的张量
data1 = torch.Tensor(2, 3)
print(data1)
"""
输出：
tensor([[0., 0., 0.],
        [0., 0., 0.]])
"""

data2 = torch.Tensor([666])
print(data2)
"""
输出：
tensor([666.])
"""

data3 = torch.Tensor([111, 666])
print(data3)
"""
输出：
tensor([111., 666.])
"""

2.1.3-torch.tensor()和torch.Tensor()

在PyTorch中，torch.tensor()和torch.Tensor()实际上是指同一件事，通常不会产生混淆。torch.tensor()是创建一个新的PyTorch张量（Tensor）的函数，而torch.Tensor是张量对象的类。在实际使用中，torch.tensor()是用来创建张量的函数，而torch.Tensor通常用在类型注释或者继承中。

1. torch.tensor()：
   • 这是一个函数，用于创建一个新的PyTorch张量。它接受各种类型的输入数据（如列表、NumPy数组、标量等），并将它们转换成PyTorch张量。
   • 例如：torch.tensor([1, 2, 3])会创建一个包含元素1, 2, 3的一维张量。
2. torch.Tensor：
   • 这是一个类，代表了PyTorch中的张量数据类型。
   • 在大多数情况下，你不会直接使用torch.Tensor()来创建张量，因为这样做需要传递一个数据对象，而且通常使用torch.tensor()更为方便。
   • 但是，torch.Tensor可以在类型注释中使用，以表明一个函数的参数或返回值是PyTorch张量类型。
   • 另外，如果你想要创建一个特定类型的张量（例如，指定了数据类型或设备的张量），你可能会直接使用torch.Tensor的构造函数。

2.1.4-创建线性和随机张量

torch.arange 和 torch.linspace 创建线性张量

torch.randn 创建随机张量

data1 = torch.arange(0, 8, 2)
print(data1)
"""
tensor([0, 2, 4, 6])
"""

data2 = torch.linspace(0, 10, 5)
print(data2)
"""
tensor([ 0.0000,  2.5000,  5.0000,  7.5000, 10.0000])
"""

data3 = torch.randn(3, 5)
print(data3)
"""
tensor([[ 1.1598, -1.3089, -0.4497,  0.3560, -1.1106],
        [ 0.8603,  0.3001, -0.7244,  0.9294, -0.1535],
        [ 0.6036, -1.1146, -0.7932, -1.2622, -0.9836]])
"""

• data1 = torch.arange(0, 8, 2)：使用torch.arange()函数创建一个从0开始，到8结束（不包括8），步长为2的一维张量。

• 输出结果为：tensor([0, 2, 4, 6])，这是一个包含0, 2, 4, 6的张量。

• data2 = torch.linspace(0, 10, 5)：使用torch.linspace()函数创建一个在0到10之间均匀分布的5个元素的一维张量。

• 输出结果为：tensor([0.0000, 2.5000, 5.0000, 7.5000, 10.0000])，这是一个包含0, 2.5, 5, 7.5, 10的张量。

• data3 = torch.randn(3, 5)：使用torch.randn()函数创建一个3行5列的二维张量，其中的元素是从标准正态分布（均值为0，方差为1）中随机采样的。

• 输出结果为一个3x5的矩阵，其中的元素是随机生成的，每次运行代码时都会不同。

2.1.5-创建0&1&指定值张量

torch.ones 创建全1张量

torch.zeros 创建全0张量

torch.full 创建全为指定值张量

这些函数提供了一种快速创建具有特定值的张量的方法，这些张量可以用于初始化、占位、填充、算法实现等多种场景。它们是深度学习和科学计算中常用的工具，因为它们可以简化代码并提高效率。

# torch.zeros() 创建全0张量
data1 = torch.zeros(2, 4)
print(data1)
"""
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.]])
"""

# torch.ones()创建全1张量
data2 = torch.ones(2, 4)
print(data2)
"""
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.]])
"""

# 创建指定值张量
data3 = torch.full([2, 4], 666)
print(data3)
"""
tensor([[666, 666, 666, 666],
        [666, 666, 666, 666]])
"""

2.1.6-张量元素类型转换

data3 = torch.full([2, 4], 666)
print(data3.dtype)
"""
torch.int64
"""
data4 = data3.type(torch.float64)
print(data4.dtype)
"""
torch.float64
"""
data5 = data3.type(torch.int)
print(data5.dtype)
"""
torch.int32
"""

2.2. 张量的类型转换

2.2.1-张量转换为NumPy数组

data1 = torch.tensor([1, 2, 3])
print(data1)  # tensor([1, 2, 3])

data_np = data1.numpy()
print(data_np)  # [1 2 3]

print(type(data1))  # <class 'torch.Tensor'>
print(type(data_np))  # <class 'numpy.ndarray'>

2.2.2-NumPy数组转换为张量

data_np = np.array([1, 2, 3, 4])
print(data_np)  # [1 2 3 4]

data_tensor = torch.from_numpy(data_np)
print(data_tensor)  # tensor([1, 2, 3, 4], dtype=torch.int32)

print(type(data_np))  # <class 'numpy.ndarray'>
print(type(data_tensor))  # <class 'torch.Tensor'>

data_tensor2 = torch.tensor(data_np)
print(data_tensor2)  # tensor([1, 2, 3, 4], dtype=torch.int32)
print(type(data_tensor2))  # <class 'torch.Tensor'>

2.2.3-标量张量和数字转换

data = torch.tensor([666, ])
print(data.item())  # 666
data2 = torch.tensor(666)
print(data2.item())  # 666

3.张量的数值运算

3.1-张量基本运算

• add() +

• sub() -

• mul() *

• div() /

• neg() 正负数取反

函数不影响原始数据值

data = torch.randint(0, 10, [2, 4])
print(data)
"""
tensor([[9, 0, 3, 0],
        [5, 7, 2, 4]])
"""
print(data.add(10))
"""
tensor([[19, 10, 13, 10],
        [15, 17, 12, 14]])
"""

print(data.sub(10))
"""
tensor([[ -1, -10,  -7, -10],
        [ -5,  -3,  -8,  -6]])
"""

print(data.mul(10))
"""
tensor([[90,  0, 30,  0],
        [50, 70, 20, 40]])
"""

print(data.div(10))
"""
tensor([[0.9000, 0.0000, 0.3000, 0.0000],
        [0.5000, 0.7000, 0.2000, 0.4000]])
"""

print(data.neg())
"""
tensor([[-9,  0, -3,  0],
        [-5, -7, -2, -4]])

"""

• 加入下划线后将会修改原数据

  • add_() +

  • sub_() -

  • mul_() *

  • div_() /

  • neg_() 正负数取反

data = torch.randint(0, 10, [2, 4])
print(data)
"""
tensor([[9, 4, 4, 3],
        [0, 4, 6, 8]])
"""

print(data.add_(10))
"""
tensor([[19, 14, 14, 13],
        [10, 14, 16, 18]])
"""

print(data)
"""
tensor([[19, 14, 14, 13],
        [10, 14, 16, 18]])
"""

3.2-张量乘法运算

• 点乘运算

点乘指（Hadamard）的是两个同维数组对应位置的元素相乘，使用mul 和运算符 * 实现

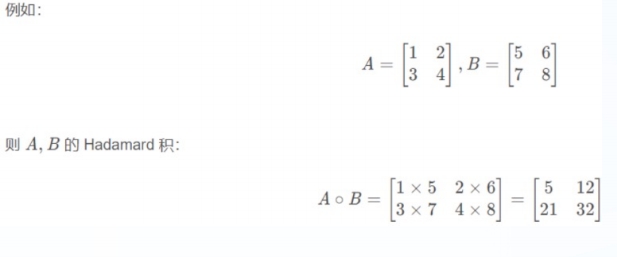
data1 = torch.tensor([[1, 2], [3, 4]])
data2 = torch.tensor([[2, 2], [3, 3]])

data_mul = torch.mul(data1, data2)
print(data_mul)
"""
tensor([[ 2,  4],
        [ 9, 12]])
"""

data_cheng = data1 * data2
print(data_cheng)
"""
tensor([[ 2,  4],
        [ 9, 12]])
"""

• 乘法运算
  • 数组乘法运算要求第一个数组 shape: (n, m)，第二个数组 shape: (m, p), 两个数组乘法运算 shape 为: (n, p)。
  • 运算符 @ 用于进行两个矩阵的乘积运算
  • torch.matmul 中输入的 shape 不同的张量, 对应的维度必须符合数组乘法的运算规则

data1 = torch.tensor([[1, 2], [3, 4], [6, 7], [7, 8]])
data2 = torch.tensor([[2, 5], [3, 6]])

data_new1 = data1 @ data2
print(data_new1)
"""
tensor([[ 8, 17],
        [18, 39],
        [33, 72],
        [38, 83]])
"""

data_new2 = torch.matmul(data1, data2)
print(data_new2)
"""
tensor([[ 8, 17],
        [18, 39],
        [33, 72],
        [38, 83]])
"""

在这段代码中，data_new1 = data1 @ data2 表示对两个张量 data1 和 data2 进行矩阵乘法（也称为点乘或内积）。矩阵乘法的计算方式如下：

给定两个矩阵 A 和 B，其中 A 的维度为 m×n，B 的维度为 n×p，它们的乘积 C 的维度将是 m×p，C 中的每个元素 c_ij 是通过取 A 的第 i 行与 B 的第 j 列的点积得到的。

具体来说，对于 data1 和 data2：

data1 是一个 4x2 的矩阵：

[[1, 2],
 [3, 4],
 [6, 7],
 [7, 8]]

data2 是一个 2x2 的矩阵：

[[2, 5],
 [3, 6]]

计算结果 data_new1 的每个元素是通过以下方式计算的：

• 第一行第一列的元素：data1 的第一行 [1, 2] 与 data2 的第一列 [2, 3] 的点积：
  ( (1 × 2) + (2 × 3) = 2 + 6 = 8 )

• 第一行第二列的元素：data1 的第一行 [1, 2] 与 data2 的第二列 [5, 6] 的点积：
  ( (1 × 5) + (2× 6) = 5 + 12 = 17 )

• 第二行第一列的元素：data1 的第二行 [3, 4] 与 data2 的第一列 [2, 3] 的点积：
  ( (3 × 2) + (4 × 3) = 6 + 12 = 18 )

• 第二行第二列的元素：data1 的第二行 [3, 4] 与 data2 的第二列 [5, 6] 的点积：
  ( (3 ×5) + (4 × 6) = 15 + 24 = 39 )

以此类推，计算出 data_new1 的所有元素。

最终得到的 data_new1 是一个 4x2 的矩阵：

[[ 8, 17],
[18, 39],
[33, 72],
[38, 83]]

这就是 data_new1 的计算过程。

3.3-张量的运算函数

• 均值

• 平方根

• 求和

• 指数计算

• 对数计算等等

data = torch.randint(0, 10, [1, 3], dtype=torch.float64)
print(data)  # tensor([[4., 4., 3.]], dtype=torch.float64)

# 平均
print(data.mean())  # tensor(3.6667, dtype=torch.float64)

# 求和
print(data.sum())  # tensor(11., dtype=torch.float64)

# 平方数
print(torch.pow(data, 2))  # tensor([[16., 16.,  9.]], dtype=torch.float64)

# n次方，例如3次方
print(torch.pow(data, 3))  # tensor([[64., 64., 27.]], dtype=torch.float64)

# 求平方根
print(data.sqrt())  # tensor([[2.0000, 2.0000, 1.7321]], dtype=torch.float64)

# 指数计算（e的n次方）
print(data.exp())  # tensor([[54.5982, 54.5982, 20.0855]], dtype=torch.float64)

# 对数计算
print(data.log())  # tensor([[1.3863, 1.3863, 1.0986]], dtype=torch.float64)
print(data.log10())  # tensor([[0.6021, 0.6021, 0.4771]], dtype=torch.float64)

4.张量索引介绍

4.1-简单索引、列表索引、范围索引

• 基本索引

  • 行索引： 使用行号进行索引，例如data[i]会返回第i行的元素。

  • 列索引： 使用列号和冒号进行索引，例如data[:, j]会返回第j列的所有元素。

• 组合索引

  • 行和列索引： 可以同时指定行和列进行索引，例如data[i, j]会返回位于第i行第j列的单个元素。

  • 多行多列索引： 使用逗号分隔的索引可以同时索引多行和多列，例如data[i:j, k:l]会返回从第i行到第j-1行，第k列到第l-1列的子张量。

• 列表索引

  • 使用列表索引： 可以传递一个列表来索引多个元素，例如data[[a, b], [c, d]]会返回位于(a,c)和(b,d)位置的元素。

• 布尔索引

  • 使用布尔数组索引： 可以传递一个布尔数组来索引满足条件的元素，例如data[condition]会返回所有condition为True的元素。

• 范围索引

  • 使用冒号（:）： 可以指定一个范围来索引，例如data[:n]会返回前n个元素。

• 嵌套索引

  • 使用嵌套列表索引： 可以传递一个嵌套列表来索引多个元素，例如data[[a, b], [c, d]]与列表索引类似，但使用嵌套列表。

• None索引

  • 使用None： 可以传递None来保持某个维度不变，例如data[None, :]会将张量扩展为一个新的维度。

• 索引赋值

  • 索引后赋值： 可以在索引后直接赋值，例如data[i, j] = value会将位于第i行第j列的元素设置为value。

# 使用torch.randint函数创建一个形状为4x5的四行五列张量，其中的元素是从0到9（包含0，不包含10）的随机整数。
data = torch.randint(0, 10, [4, 5])
# 简单取值
print(data)
"""
tensor([[7, 4, 6, 6, 1],
        [6, 8, 8, 0, 9],
        [7, 5, 0, 9, 7],
        [6, 2, 2, 1, 1]])
"""

print(data[0])  # tensor([7, 4, 6, 6, 1])
print(data[0, :])  # tensor([7, 4, 6, 6, 1])
# data[0]和data[0, :]都表示取出张量的第一行。data[0]是使用行索引，而data[0, :]是使用行索引和列索引（冒号表示取整行），所以一般都使用data[0]

print(data[:, 0])  # tensor([7, 6, 7, 6])
# data[:, 0]表示取出张量的第一列。冒号表示取整列，0表示列的索引

# 列表索引
print(data[[0, 1], [1, 2]])  # tensor([4, 8])
# data[[0, 1], [1, 2]]表示取出张量中位置为(0,1)和(1,2)的元素，即取出第一行的第二个元素和第二行的第三个元素。
print(data[:, [0, 1]])
# data[:, [0, 1]]表示取出张量的前两列。
"""
tensor([[7, 4],
        [6, 8],
        [7, 5],
        [6, 2]])
"""

print(data[[[0], [1]], [1, 2]])
# data[[[0], [1]], [1, 2]]表示取出张量中位置为(0,1)和(1,2)的元素，这与data[[0, 1], [1, 2]]相同，但是使用了嵌套列表。
"""
tensor([[4, 6],
        [8, 8]])
"""

# 范围索引
print(data[:3, :2])
# data[:3, :2]表示取出张量的前3行和前2列。
"""
tensor([[7, 4],
        [6, 8],
        [7, 5]])
"""

print(data[2:, :2])
# data[2:, :2]表示取出张量的第3行到最后（因为索引从0开始，2表示第三行）以及这两行的前两列。
"""
tensor([[7, 5],
        [6, 2]])
"""

4.2-多维索引

# 创建一个形状为3x4x5的三维张量
data = torch.randint(0, 10, [3, 4, 5])
print(data)
# 打印整个三维张量，可以看到它包含三个2D矩阵（每个矩阵的形状为4x5）
"""
tensor([[[8, 1, 2, 7, 1],
         [1, 2, 2, 5, 6],
         [9, 5, 8, 9, 2],
         [8, 8, 8, 8, 0]],

        [[2, 9, 8, 3, 2],
         [2, 8, 0, 5, 7],
         [9, 0, 8, 0, 0],
         [6, 0, 0, 8, 1]],

        [[1, 8, 9, 1, 5],
         [5, 0, 6, 9, 8],
         [8, 8, 1, 3, 2],
         [3, 2, 3, 1, 4]]])
"""

print(data[0, :, :])
# data[0, :, :]表示取出张量的第一个“层”（或者说第一个3D切片），即第一组4x5的矩阵。这里的:表示选取该维度的所有元素。
"""
tensor([[8, 1, 2, 7, 1],
        [1, 2, 2, 5, 6],
        [9, 5, 8, 9, 2],
        [8, 8, 8, 8, 0]])
"""

print(data[:, 0, :])
# data[:, 0, :]表示取出张量中每个“层”的第一个“行”（或者说第一个4D切片），即取出所有层的第一行。这里的0表示第一个元素的索引。
"""
tensor([[8, 1, 2, 7, 1],
        [2, 9, 8, 3, 2],
        [1, 8, 9, 1, 5]])
"""

print(data[:, :, 0])
# data[:, :, 0]表示取出张量中每个“层”的第一个“元素”（或者说第一个3D切片），即取出所有层的第一列。这里的0表示第一个元素的索引。
"""
tensor([[8, 1, 9, 8],
        [2, 2, 9, 6],
        [1, 5, 8, 3]])
"""

在多维数据处理中，这样的索引操作非常有用，它们允许你快速访问和操作数据的特定部分。例如，在处理图像数据时，你可能需要访问特定通道的所有像素，或者在处理时间序列数据时，你可能需要访问特定时间点的所有特征。这些操作使得这些任务变得简单而高效。

5.张量形状操作

5.1-reshape()函数-重塑形状

reshape()函数：

• reshape()函数用于改变张量的形状，而不改变其数据。如果新形状与原始张量不兼容（即元素总数不同），则会抛出错误。
• 例如：x = torch.randn(2, 3) 创建一个2x3的张量，x.reshape(3, 2) 将其重塑为3x2的张量。

data = torch.tensor([[1, 2, 3], [5, 6, 7]])
print(data.shape)  # torch.Size([2, 3])

data_shape1 = data.reshape(1, 6)
print(data_shape1)  # tensor([[1, 2, 3, 5, 6, 7]])
print(data_shape1.shape)  # torch.Size([1, 6])
data_shape2 = data.reshape(6, 1)
print(data_shape2)
"""
tensor([[1],
        [2],
        [3],
        [5],
        [6],
        [7]])
"""
print(data_shape2.shape)  # torch.Size([6, 1])

5.2-squeeze()和unsqueeze()函数-降维升维

squeeze()函数：

• squeeze()函数用于去除张量中所有长度为1的维度。如果指定了维度，则只去除指定的维度中长度为1的维度。
• 例如：x = torch.randn(2, 1, 3)，x.squeeze() 将其变为 torch.randn(2, 3)，因为去除了长度为1的第二维。

unsqueeze()函数：

• unsqueeze()函数用于在指定位置添加一个长度为1的新维度。这对于增加张量的维度数量很有用，尤其是在需要满足某些操作的维度要求时。
• 例如：x = torch.randn(2, 3)，x.unsqueeze(1) 将其变为 torch.randn(2, 1, 3)，在第二维添加了一个长度为1的新维度。

data = torch.tensor([1, 2, 3, 4, 5])
print(data.shape)

print(data.unsqueeze(1).shape)
print(data.unsqueeze(1).squeeze().shape)

• data是一个一维张量，所以它的形状（shape）是torch.Size([5])，表示这个张量有5个元素。

• data.unsqueeze(1)在索引为1的位置（即在第一个维度的后面）添加了一个长度为1的新维度。因为原始张量是一维的，所以这个操作将其变为一个二维张量，形状变为torch.Size([5, 1])。

• data.unsqueeze(1)将张量变为torch.Size([5, 1])。然后，squeeze()函数移除了所有长度为1的维度。由于这个张量只有一个长度为1的维度，squeeze()将其移除，张量恢复到原始的一维形状，即torch.Size([5])。

5.3-transpose()和permute()函数

transpose()函数：

• transpose()函数用于交换张量的两个维度。它接受两个参数，分别是要交换的维度的索引。
• 例如：x = torch.randn(2, 3)，x.transpose(0, 1) 将其变为 torch.randn(3, 2)，即交换了第一维和第二维。

permute()函数：

• permute()函数用于重新排列张量的维度。它接受一系列维度索引作为参数，并按照这些索引重新排列张量的维度。
• 例如：x = torch.randn(2, 3, 4)，x.permute(1, 2, 0) 将其变为 torch.randn(3, 4, 2)，即重新排列了维度的顺序。

# 创建一个形状为(2, 3, 4)的三维张量
data = torch.randn(2, 3, 4)

# 这个函数交换张量的第0维和第1维。在形状上，这意味着交换第一个数字和第二个数字：
transposed_data = torch.transpose(data, 0, 1)
print(transposed_data.shape)  # 输出: torch.Size([3, 2, 4])

# 我们对data应用了torch.transpose(data, 0, 1)，得到形状为(3, 2, 4)的张量。然后，我们再次应用torch.transpose，这次交换第1维和第2维：
transposed_data_again = torch.transpose(transposed_data, 1, 2)
print(transposed_data_again.shape)  # 输出: torch.Size([3, 4, 2])

# 这个函数重新排列张量的维度，按照给定的索引顺序。索引[1, 2, 0]意味着我们取第1维作为新的第0维，第2维作为新的第1维，第0维作为新的第2维：
permuted_data = torch.permute(data, [1, 2, 0])
print(permuted_data.shape)  # 输出: torch.Size([3, 4, 2])

# 这与torch.permute(data, [1, 2, 0])相同，但是使用张量对象自身的permute方法
permuted_data_self = data.permute([1, 2, 0])
print(permuted_data_self.shape)  # 输出: torch.Size([3, 4, 2])

5.4-view()和contiguous()函数

view()函数：

• view()函数用于改变张量的形状，类似于reshape()，但它要求张量在内存中是连续的。如果不连续，需要先调用contiguous()方法。
• 例如：x = torch.randn(2, 3)，x.view(3, 2) 将其变为3x2的张量。

contiguous()函数：

• contiguous()函数用于确保张量在内存中是连续的。有些操作可能会使张量在内存中不连续，这时候如果需要使用view()，就必须先调用contiguous()。
• 例如：x = torch.randn(2, 3).transpose(0, 1) 后，x在内存中不连续，x.contiguous() 会返回一个新的连续张量。

data = torch.tensor([[10, 20, 30], [40, 50, 60]])
print(data)
"""
tensor([[10, 20, 30],
        [40, 50, 60]])
"""
print(data.shape)
# torch.Size([2, 3])

print(data.is_contiguous())
# True

print(data.view(3, 2))
"""
tensor([[10, 20],
        [30, 40],
        [50, 60]])
"""

6.张量的拼接操作

• torch.cat()

将两个张量根据指定的维度拼接起来，不改变维度数

data1 = torch.randint(0, 10, [1, 2, 3])
data2 = torch.randint(0, 10, [1, 2, 3])
print(data1)
"""
tensor([[[4, 1, 8],
         [2, 8, 1]]])
"""
print(data2)
"""
tensor([[[0, 3, 1],
         [4, 2, 2]]])
"""
# 按0维度拼接
data_0 = torch.cat([data1, data2], dim=0)
print(data_0)
"""
tensor([[[4, 1, 8],
         [2, 8, 1]],

        [[0, 3, 1],
         [4, 2, 2]]])
"""

# 按1维度拼接
data_1 = torch.cat([data1, data2], dim=1)
print(data_1)
"""
tensor([[[4, 1, 8],
         [2, 8, 1],
         [0, 3, 1],
         [4, 2, 2]]])
"""

# 按2维度拼接
data_2 = torch.cat([data1, data2], dim=2)
print(data_2)
"""
tensor([[[4, 1, 8, 0, 3, 1],
         [2, 8, 1, 4, 2, 2]]])
"""

7.自动微分模块

PyTorch的一个核心特性是自动微分（Automatic Differentiation），它允许我们自动计算梯度，这对于训练深度学习模型至关重要。

• 张量（Tensor）：PyTorch中的基本数据结构，可以看作是一个多维数组。
• 梯度（Gradient）：在数学中，梯度是一个向量，指向函数增长最快的方向。在深度学习中，梯度用于更新模型参数。
• 反向传播（Backpropagation）：一种通过计算梯度来更新网络权重的技术。
• 计算图（Computation Graph）：一个有向图，其中的节点表示操作，边表示数据（张量）流动的方向。

微分逻辑：

# 创建一个张量，并设置requires_grad=True来追踪其梯度
x = torch.tensor(2.0, requires_grad=True)

# 执行一些操作
y = x * x
z = y * y

# 计算z关于x的梯度
z.backward()

# 输出x的梯度
print(x.grad)  # tensor(32.)  梯度32

使用案例帮助理解功能

import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的线性模型
model = nn.Linear(1, 1)

# 定义损失函数
loss_fn = nn.MSELoss()

# 定义优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 一些模拟数据
x = torch.tensor([[1.0], [2.0], [3.0]], dtype=torch.float32)
y = torch.tensor([[2.0], [4.0], [6.0]], dtype=torch.float32)

# 训练模型
for epoch in range(100):
    # 前向传播
    pred = model(x)
    loss = loss_fn(pred, y)

    # 反向传播和优化
    optimizer.zero_grad()  # 清零梯度
    loss.backward()  # 反向传播
    optimizer.step()  # 更新参数

    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/100], Loss: {loss.item():.4f}')
        
"""
Epoch [10/100], Loss: 2.0538
Epoch [20/100], Loss: 0.4096
Epoch [30/100], Loss: 0.2430
Epoch [40/100], Loss: 0.2175
Epoch [50/100], Loss: 0.2060
Epoch [60/100], Loss: 0.1962
Epoch [70/100], Loss: 0.1869
Epoch [80/100], Loss: 0.1781
Epoch [90/100], Loss: 0.1698
Epoch [100/100], Loss: 0.1618
"""

定义一个简单的线性模型model，一个损失函数loss_fn，以及一个优化器optimizer。然后，我们使用模拟数据x和y来训练模型。在每个epoch中，我们首先进行前向传播，计算损失，然后进行反向传播和参数更新。

8.pytorch示例代码理解

8.1-线性回归

需要自行安装涉及的numpy、matplotlib模块

#!/usr/bin/env python3
# -*- coding:utf-8 -*-
# @Project  :hello-algo-main
# @File     :xianxinghuigui.py
# @Time     :2024-11-14 18:29
# @Author   :wangting_666

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt

# 设置随机种子，保证结果可复现
torch.manual_seed(0)
np.random.seed(0)

# 生成线性回归的数据
x = torch.linspace(-1, 1, 100).reshape(-1, 1)  # 生成从 -1 到 1 的 100 个点
y = 3 * x + 2 + torch.randn(x.size(0), 1) * 0.3  # 真实的线性关系加上一些噪声


# 定义线性回归模型
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # 1 输入特征，1 输出特征

    def forward(self, x):
        return self.linear(x)


# 实例化模型、定义损失函数和优化器
model = LinearRegressionModel()
criterion = nn.MSELoss()  # 均方误差损失
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 使用SGD优化器

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    model.train()

    # 前向传播
    outputs = model(x)
    loss = criterion(outputs, y)  # 计算损失

    # 反向传播和优化
    optimizer.zero_grad()  # 清空梯度
    loss.backward()  # 计算梯度
    optimizer.step()  # 更新参数

    # 每 100 次输出一次损失
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

# 评估模型
with torch.no_grad():
    model.eval()  # 切换到评估模式
    predicted = model(x)

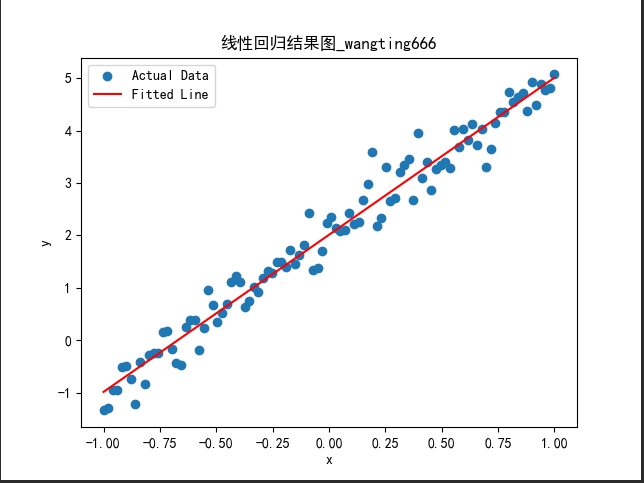
    # 绘制数据和拟合的直线
    plt.scatter(x.numpy(), y.numpy(), label='Actual Data')
    plt.plot(x.numpy(), predicted.numpy(), color='red', label='Fitted Line')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.title('线性回归结果图_wangting666')
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.legend()
    plt.show()

控制台输出：

Epoch [100/1000], Loss: 1.0944
Epoch [200/1000], Loss: 0.3330
Epoch [300/1000], Loss: 0.1551
Epoch [400/1000], Loss: 0.1099
Epoch [500/1000], Loss: 0.0984
Epoch [600/1000], Loss: 0.0955
Epoch [700/1000], Loss: 0.0947
Epoch [800/1000], Loss: 0.0945
Epoch [900/1000], Loss: 0.0945
Epoch [1000/1000], Loss: 0.0945

绘图结果：

8.2-使用 GPU 加速训练

PyTorch 支持将张量和模型移动到 GPU（如果有可用的 GPU）。通过 to(device) 可以将数据或模型转移到指定的设备

import torch
import torch.nn as nn

# 检查是否有 GPU 可用
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 定义一个简单的神经网络
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(2, 4)
        self.fc2 = nn.Linear(4, 1)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x

# 初始化模型
model = SimpleNN().to(device)

# 创建输入数据并将其也转移到 GPU
input_data = torch.tensor([[1.0, 2.0]]).to(device)

# 进行前向传播
output = model(input_data)
print("模型输出:\n", output)

输出：

模型输出:
 tensor([[0.2424]], grad_fn=<AddmmBackward0>)

通过 device = torch.device('cuda') 检查是否有可用的 GPU，并通过 .to(device) 将模型和数据迁移到 GPU 上。这样可以加速计算。

8.3-图片识别

官方素材 ：https://download.pytorch.org/tutorial/faces.zip
数据存于“data / faces /”的目录中

这个数据集实际上是imagenet数据集标注为face的图片当中在 dlib 面部检测 (dlib’s pose estimation) 表现良好的图片。我们要处理的是一个面部姿态的数据集

#!/usr/bin/env python3
# -*- coding:utf-8 -*-
# @Project  :hello-algo-main
# @File     :test03.py
# @Time     :2024-11-14 19:03
# @Author   :wangting_666

from __future__ import print_function, division
import os
import torch
import pandas as pd 
from skimage import io, transform 
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils

# 注意skimage包的安装名<scikit-image>,安装方式： pip install scikit-image -i https://pypi.tuna.tsinghua.edu.cn/simple


# 忽略警告
import warnings

warnings.filterwarnings("ignore")

plt.ion()

landmarks_frame = pd.read_csv('data/faces/face_landmarks.csv')

n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].values
landmarks = landmarks.astype('float').reshape(-1, 2)

print('Image name: {}'.format(img_name))
print('Landmarks shape: {}'.format(landmarks.shape))
print('First 4 Landmarks: {}'.format(landmarks[:4]))


def show_landmarks(image, landmarks):
    """匹配显示出csv中带有地标的对应图片"""
    plt.imshow(image)
    plt.scatter(landmarks[:, 0], landmarks[:, 1], s=10, marker='.', c='r')
    plt.pause(0.001)

plt.figure()
show_landmarks(io.imread(os.path.join('data/faces/', img_name)), landmarks)
plt.show()

控制台输出：

Image name: person-7.jpg
Landmarks shape: (68, 2)
First 4 Landmarks: [[32. 65.]
 [33. 76.]
 [34. 86.]
 [34. 97.]]

绘图如下：

根据计算的结果比对face_landmarks.csv

可以看到结果和图片集中能匹配上person-7.jpg文件的图形