7.高可用集群架构Keepalived双主热备原理

news2024/11/17 11:05:03

一. 高可用集群架构Keepalived双主热备原理

在这里插入图片描述
在这里插入图片描述

（1）主机+备机keepalived配置(192.168.1.171)

! Configuration File for keepalived

global_defs {
   
   # 路由id:当前安装keepalived节点主机的标识符，全局唯一
   router_id keep_101
}
#计算机节点(主机配置)
vrrp_instance VI_1 {
   </

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2242121.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

深入理解接口测试：实用指南与最佳实践5.0（二）

深入理解接口测试：实用指南与最佳实践5.0（二）

✨博客主页&#xff1a; https://blog.csdn.net/m0_63815035?typeblog &#x1f497;《博客内容》&#xff1a;.NET、Java.测试开发、Python、Android、Go、Node、Android前端小程序等相关领域知识 &#x1f4e2;博客专栏&#xff1a; https://blog.csdn.net/m0_63815035/cat…
阅读更多...
TypeScript简介：TypeScript是JavaScript的一个超集

TypeScript简介：TypeScript是JavaScript的一个超集

官方描述&#xff1a;TypeScript 是 JavaScript 的一个超集 GitHub官网&#xff1a;https://github.com/Microsoft/TypeScript TypeScript is a superset of JavaScript that compiles to clean JavaScript output. TypeScript 是 JavaScript 的一个超集&#xff0c;支持 EC…
阅读更多...
【计算机网络】UDP网络程序

【计算机网络】UDP网络程序

一、服务端 1.udpServer.hpp 此文件负责实现一个udp服务器 #pragma once#include <iostream> #include <string> #include <cstdlib> #include <cstring> #include <functional> #include <strings.h> #include <unistd.h> #incl…
阅读更多...
【启明智显分享】5G CPE与5G路由器到底有什么区别？

【启明智显分享】5G CPE与5G路由器到底有什么区别？

5G路由器和5G CPE在功能和应用场景上存在很明显的差异&#xff0c;小编做了详细比较&#xff0c;希望能帮助到你进一步了解他们的区别及应用。 一、定义与功能 5G路由器 5G路由器是一个将5G网络连接转换为Wi-Fi信号的设备&#xff0c;使多个Wi-Fi设备可以通过5G网络进行连接…
阅读更多...
对称加密与非对称加密：密码学的基石及 RSA 算法详解

对称加密与非对称加密：密码学的基石及 RSA 算法详解

对称加密与非对称加密&#xff1a;密码学的基石及 RSA 算法详解 在当今数字化的时代&#xff0c;信息安全至关重要。对称加密和非对称加密作为密码学中的两种基本加密技术&#xff0c;为我们的数据安全提供了强大的保障。本文将深入探讨对称加密和非对称加密的特点、应用场景&…
阅读更多...
爬虫——数据解析与提取

爬虫——数据解析与提取

第二节&#xff1a;数据解析与提取 在网络爬虫开发中&#xff0c;获取网页内容&#xff08;HTML&#xff09;是第一步&#xff0c;但从这些内容中提取有用的数据&#xff0c;才是爬虫的核心部分。HTML文档通常结构复杂且充满冗余信息&#xff0c;因此我们需要使用高效的解析工…
阅读更多...
我们是如何实现 TiDB Cloud Serverless 的 - 成本篇

我们是如何实现 TiDB Cloud Serverless 的 - 成本篇

作者&#xff1a; shiyuhang0 原文来源&#xff1a; https://tidb.net/blog/fbedeea4 背景 Serverless 数据库是云原生时代的产物&#xff0c;它提供全托管&#xff0c;按需付费&#xff0c;自动弹性的云数据库服务&#xff0c;让客户免于繁重的数据库运维工作。关于 Serve…
阅读更多...
Linux——环境基础开发工具使用2（正在更新中...）

Linux——环境基础开发工具使用2（正在更新中...）

1.自动化构建-make/Makefile 1.1 认识make和Makefile make是一个命令&#xff1b; Makefile是一个文件。 1.2 理解 其中在第一个图片中&#xff0c;第一行的 mytest:test.c 叫做依赖关系&#xff1b;第二行的 gcc test.c -o mytest 叫做依赖方法。 依赖关系和依赖方法共同…
阅读更多...
微服务链路追踪skywalking安装

微服务链路追踪skywalking安装

‌SkyWalking是一个开源的分布式追踪系统&#xff0c;主要用于监控和分析微服务架构下的应用性能。‌ 它提供了分布式追踪、服务网格遥测分析、度量聚合和可视化一体化解决方案&#xff0c;特别适用于微服务、云原生架构和基于容器的环境&#xff08;如Docker、K8s、Mesos&…
阅读更多...
品牌如何利用大数据工具，进行消费者洞察分析？

品牌如何利用大数据工具，进行消费者洞察分析？

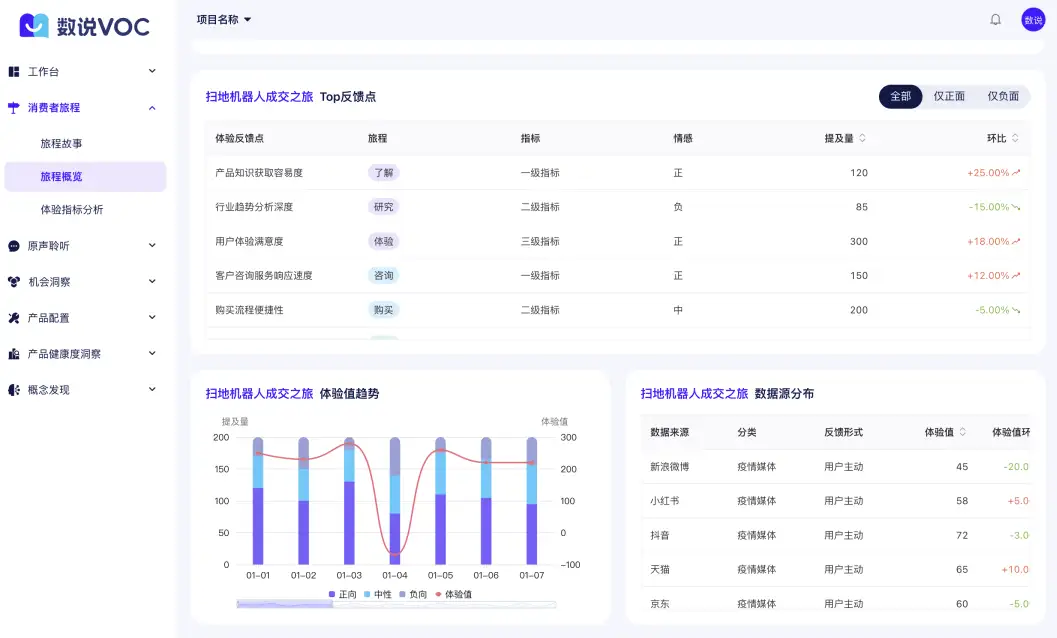
存量竞争的时代&#xff0c; 消费者聆听是品牌持续增长的关键&#xff0c;借助大数据的消费者数据洞察&#xff0c;可以帮助品牌分析消费者的所思所想及行为特征&#xff0c;获取消费者对产品的需求痛点、使用感受&#xff0c;对品牌的评价口碑等&#xff0c;从而帮助品牌更好地…
阅读更多...
模拟实现优先级队列

模拟实现优先级队列

目录 定义 特点 构造函数 常用方法 关于扩容的问题 关于建堆的问题 向上调整和向下调整的比较 &#xff08;向上调整&#xff09;代码 &#xff08;向下调整&#xff09;代码 关于入队列和出队列问题 模拟实现优先级队列代码 关于堆排序的问题 堆排序代码 关于对…
阅读更多...
【4】GD32H7xx ADC采样

【4】GD32H7xx ADC采样

目录 1. GD32H7xx ADC1.1 ADC外设资源1.2 采样时间1.3 片上硬件过采样 2. ADC DMA规则多通道采样程序3. 程序测试 1. GD32H7xx ADC 1.1 ADC外设资源 GD32H7xx 有3个ADC外设&#xff1a; ADC0 20个外部通道&#xff0c;1个内部通道&#xff08;DAC0_OUT0通道&#xff09;32位…
阅读更多...
GitLab 如何跨版本升级？

GitLab 如何跨版本升级？

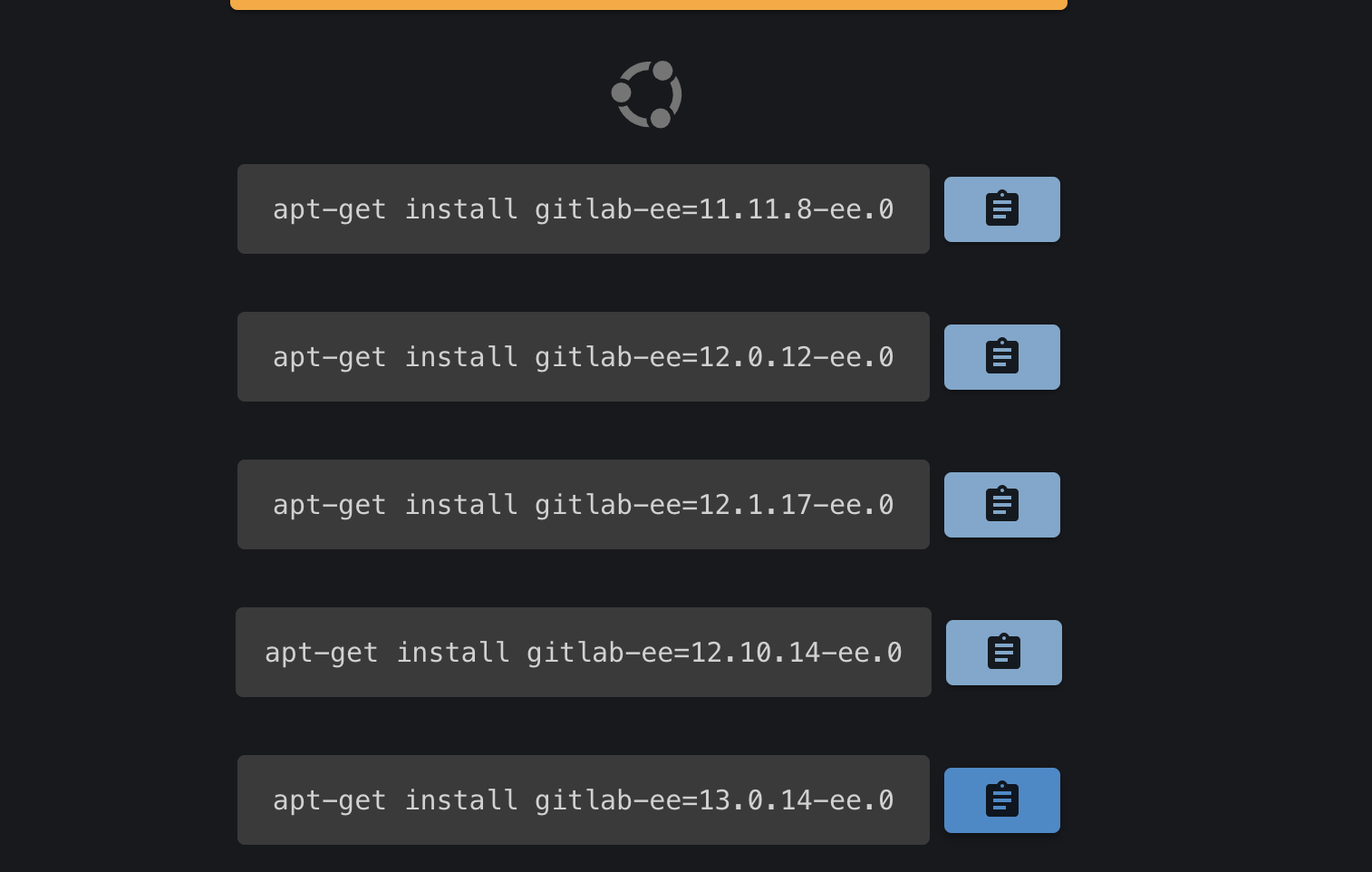
本分分享 GitLab 跨版本升级的一些注意事项。 众所周知&#xff0c;GitLab 的升级必须要严格遵循升级路径&#xff0c;否则就会出现问题&#xff0c;导致升级失败。因此&#xff0c;在 GitLab 升级之前需要做好两件事情&#xff1a; 当前版本的确认升级路径的确认 极狐GitLa…
阅读更多...
【咕泡P5人工智能CV 技术NLP项目实战】

【咕泡P5人工智能CV 技术NLP项目实战】

人工智能核心代码&#xff1a; 一、什么是人工智能技术&#xff1a; 人工智能&#xff08;Aritificial Intelligence&#xff09;&#xff0c;英文缩写AI&#xff0c;人工智能是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。 人工智…
阅读更多...
R门 - rust第一课陈天 -内存知识学习笔记

R门 - rust第一课陈天 -内存知识学习笔记

内存 #mermaid-svg-1NFTUW33mcI2cBGB {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-1NFTUW33mcI2cBGB .error-icon{fill:#552222;}#mermaid-svg-1NFTUW33mcI2cBGB .error-text{fill:#552222;stroke:#552222;}#merm…
阅读更多...
C# x Unity 从玩家控制类去分析命令模式该如何使用

C# x Unity 从玩家控制类去分析命令模式该如何使用

本文部分内容出自游戏编程模式一书,游戏编程模式,有兴趣的小伙伴可以去看看,虽然不是unity x c#写的 但是思路挺好的 目录 目录 0.先说结论 发现问题 命令模式如何解耦 打个断点更利于分析 怎么实现延迟命令? 如何撤销命令? 脚本整体一览 不足分析(AI) 0.先说结论 …
阅读更多...
【C++】—— stack和queue的模拟实现

【C++】—— stack和queue的模拟实现

前言 ​ stack 和 queue使用起来都非常简单&#xff0c;现在来模拟实现一下&#xff0c;理解其底层的原理。 ​ 在实现之前&#xff0c;应该知道&#xff0c;stack 和 queue 都是容器适配器&#xff0c;通过看官网文件也可以看出来&#xff1b;其默认的容器都是deque&#xff…
阅读更多...
探索高效的 Prompt 框架：RBTR 提示框架的奥秘与优势

探索高效的 Prompt 框架：RBTR 提示框架的奥秘与优势

前言 在当今数字化的时代&#xff0c;人工智能&#xff08;AI&#xff09;已经成为我们生活和工作中不可或缺的一部分。而 Prompt 作为与 AI 交互的关键工具&#xff0c;其质量直接影响着我们获取信息的准确性和有用性。今天&#xff0c;我们将深入探讨一个通用的 Prompt 框架…
阅读更多...
动态规划-完全背包问题——322.零钱兑换

动态规划-完全背包问题——322.零钱兑换

1.题目解析 题目来源 322.零钱兑换——力扣 测试用例 2.算法原理 1.状态表示 这里需要寻找硬币使总面值等于一个值求出所需硬币的最小个数&#xff0c;所以不妨设置一个二维dp表&#xff0c;即dp[i][j]&#xff1a;在[1,i]个硬币中选择的硬币总面值完全等于j时所需要的最小硬…
阅读更多...
day-82 最少翻转次数使二进制矩阵回文 I

day-82 最少翻转次数使二进制矩阵回文 I

思路 依次计算使行回文和列回文的的翻转次数&#xff0c;返回较小的次数即可 解题过程 计算行翻转次数&#xff1a;对于每一行&#xff0c;如果第一个数与最后一个数不相同&#xff08;前提前一个数的索引小于后一个数的索引&#xff09;则需翻转一次&#xff0c;将所有行翻转…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023