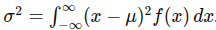关于圆周率
大约20年前的2005年,我在上大学的时候,网上流传这样一段程序,被称之为“外星人计算圆周率程序”。程序如下:
long a = 10000, b, c = 2800, d, e, f[2801], g;
main() {for (; b - c;) f[b++] = a / 5;
for (; d = 0, g = c * 2; c -= 14, printf("%.4d", e + d / a), e = d % a)
for (b = c; d += f[b] * a, f[b] = d % --g, d /= g--, --b; d *= b); scanf("%s");}
这一段C语言的程序仅仅用了4行代码,就计算出圆周率![]() 的前800位,
的前800位,
31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185
当时不由得为其赞叹。对圆周率的展开式的研究,可以帮助认识到底什么是圆,或者说圆的结构到底是什么样的,于是一场探求圆的真相的旅程就此开始了。
二十年后,让我们对这个旅程做一个阶段性的总结。
据说这个代码的的算法来自于沃里斯乘积,
![]()
但这一点终未能证实。不过这并不影响我们的分析,因为具体分析代码,可以得到,

两边都除以2,得到,

我们目前只关心![]() 即可,因为它是某种“单位”,而它的倍数只是简单的乘进去到每一项即可。此外,它还有其它的写法,比如把嵌套展开,
即可,因为它是某种“单位”,而它的倍数只是简单的乘进去到每一项即可。此外,它还有其它的写法,比如把嵌套展开,
![]()
写成求和的形式,
![]()
我们的问题不在于它是什么形式,而是在于这个形式到底代表了什么意思。
先前在“楼梯悖论”中讨论过复平面和平面直角坐标系的差别。简单说,就是复平面是有“旋向”的,而平面直角坐标系则可以认为是两个旋向同时存在且是相互等价的。正如图论中的有向图节点之间的边是有源和宿之分的,而无向图节点之间的边只起到链接节点构成关系的作用。为了简化问题,我们只讨论复平面的正旋向,而不考虑另一个旋转的方向。
在复平面中,我们画出坐标系:实轴正半轴的单位位1,也就是
![]()
虚轴的正半轴的单位为![]() ,也就是,
,也就是,
![]()
实轴的负半轴的单位为-1,也就是
![]()
虚轴的负半轴单位为![]() ,也就是
,也就是![]()
然后就转回到实轴的正半轴了。这四个值,看上去都是单位,但是实际上单位的大小大相径庭。我们知道虚数单位代表着周期,它可以非常大,相对于实轴正半轴的单位1来说,虚轴正半轴的单位可以认为是无穷大(决定于![]() 的大小),而实轴负半轴又是这个无穷大的平方那么大,以及虚轴负半轴又是这个无穷大的立方那么大,这些都是“单位”,但是一个比一个大得多。所以实际上复平面按照其实际数量来说,并不是像它看上去那么方方正正的,而是遵循渐开线的原则逐渐扩展的,而且相邻两个维数之间构成的单位方格也不是方方正正的,而是扭曲放大的。正如你所想象的,这样的图像“一点都不圆”,复制若干次旋转不同角度之后就像是星系中的多个旋臂构成的漩涡一样。
的大小),而实轴负半轴又是这个无穷大的平方那么大,以及虚轴负半轴又是这个无穷大的立方那么大,这些都是“单位”,但是一个比一个大得多。所以实际上复平面按照其实际数量来说,并不是像它看上去那么方方正正的,而是遵循渐开线的原则逐渐扩展的,而且相邻两个维数之间构成的单位方格也不是方方正正的,而是扭曲放大的。正如你所想象的,这样的图像“一点都不圆”,复制若干次旋转不同角度之后就像是星系中的多个旋臂构成的漩涡一样。
那么,到底是什么使得这个复平面显得方方正正,而中心的单位圆显得“圆”起来的呢?是观察者。比如虽然虚轴正半轴的单位比实轴正半轴长的多,但是我们知道,
![]()
![]()
![]()
![]()
所有轴的正负半轴,都符合,
![]()
也就是所有轴的单位对于虚数单位同余为0。既然如此,我们也不难想到,不仅仅是轴,复平面单位圆上的每一条半径,模上虚数单位的结果也必须是0,不然圆周上就会有“毛刺”,圆就不圆了。
所以,由此我们可以看出这样一种现实,从单位圆的实轴正向开始,辐射出的每一条“半径”,都符合
![]()
那么,我们就可以把这些“半径”的长度都列出来,
![]()
而
![]()
这就构成了半径的集合。在第一象限,半径的实际长度就是1到![]() 的自然数长度,这些长度显然都可以模1。但这不符合,
的自然数长度,这些长度显然都可以模1。但这不符合,
![]()
于是我们把所有一周的长度都乘以虚数单位![]() ,那么所有这些长度都可以模
,那么所有这些长度都可以模![]() ,这时候我们得到这些“半径”集合为,
,这时候我们得到这些“半径”集合为,
![]()
这相当于把先前的单位圆逆时针旋转了90度。以下我们用这个旋转了90度的单位圆进行讨论,以保证这些半径模![]() 都等于0(避免旋转90度之前,
都等于0(避免旋转90度之前,![]() 的情况),而且要知道四个象限的情况是中心对称的,由此我们只需要研究第一象限即可(旋转前的第二象限)。
的情况),而且要知道四个象限的情况是中心对称的,由此我们只需要研究第一象限即可(旋转前的第二象限)。
可见在这个结构中,相继两条半径的长度关系就是
![]()
的关系,而它们在平面之中又都没有![]() 而造成的毛刺,所以复平面上的单位圆实际上就是若干倍虚数单位的长度所坐落的地方,那些半径具有和实轴正半轴的不同的夹角,其实就对应于实际长度的倍数和虚数单位之间的比值。
而造成的毛刺,所以复平面上的单位圆实际上就是若干倍虚数单位的长度所坐落的地方,那些半径具有和实轴正半轴的不同的夹角,其实就对应于实际长度的倍数和虚数单位之间的比值。
最接近这一的图像就是一个螺旋楼梯:第一级台阶(半径)的长度为一个虚数单位,第二级台阶有第一个级阶两倍那么高。因为两倍的高度,它的总长度,就相当于第一级台阶长度的两倍,但是这两倍被折叠在一起,不是使得台阶变长了,而是把台阶垫高了;第三级台阶则是把三倍第一级台阶的长度折叠了两次,成为第一级台阶高度的三倍……
在垂直地面的方向上看,台阶都一样长,只是具有和初始方向不一样的夹角,但实际上若能从侧面观看,台阶一级比一级高,呈等差数列,整个高度分四个部分,第一部分高度为1到虚数单位![]() ,第二部分为虚数单位
,第二部分为虚数单位![]() 到
到![]() ,第三部分为
,第三部分为![]() 到
到![]() ,第四部分为
,第四部分为![]() 到
到![]() 。
。
现在我们要求的不是别的,而是台阶构成的单位圆的周长。因为四个部分是一样的(所以才叫单位圆),我们只需要求第一个部分的长度(也就是![]() ),然后乘以4(也就是
),然后乘以4(也就是![]() )即可。那么,我们如何求四分之一的圆周长度呢?
)即可。那么,我们如何求四分之一的圆周长度呢?
显然我们只知道虚数单位的大小![]() ,并没有给出周边长度的信息,但这里的结构给了我们提示。正如我们在求自然数全加和的时候,结构决定了即便无限仍然可以用无限对无限去求出确定的结果。
,并没有给出周边长度的信息,但这里的结构给了我们提示。正如我们在求自然数全加和的时候,结构决定了即便无限仍然可以用无限对无限去求出确定的结果。
若要求周长,就要求出每一个半径圆心另一侧的的“端点”的长度,可是这个“端点”的长度怎么求?首先我们先看半径,对于第n层楼梯,其长度为![]() ,那么垂直它的“切点”的相对(于1的)单位长度就可以写成,
,那么垂直它的“切点”的相对(于1的)单位长度就可以写成,
![]()
这个长度的真实单位是半径![]() ,所以实际的长度为,
,所以实际的长度为,
![]()
可见这也是在本地消去虚数单位的影响的一种实践,这使得半径的大小和弧长的关系脱钩了。进一步来说,而若要构成切线,则需要再加上2个点,分别放在切点两侧,这样的话长度就变成了,
![]()
也就是一个切点的长度,加上两边两个单位长度。而这个切线的长度是在切向上,我们需要的长度不是在切向上,而是在径向上,于是我们还得对它取倒数(实现正交关系),求相对长度,也就是得到,
![]()
由于在加2个点的时候,我们引入的是相对关系,所以这个径向上的长度又必须依赖一个基准,而这个基准又只能是前一个点的切向长度(圆周的弧上无全局单位,只能走一步看一步),所以到当前点的长度,则需要把先前所有的相对关系都计算到里面,才能得到这个点的实际长度(第一项不是相对关系,它只能是半径本身,所以全乘部分不包括半径本身,半径必须单独乘出来),

而从![]() 到
到![]() 所有这些点的长度的总和加上最初的基准长度也就是半径
所有这些点的长度的总和加上最初的基准长度也就是半径![]() ,就是四分之一圆周的长度,
,就是四分之一圆周的长度,

现在我们把所有的长度都缩小i![]() 倍,
倍,

把项数改成无限(把数量![]() 模糊掉)就得到了纯粹的半圆周率,
模糊掉)就得到了纯粹的半圆周率,
![]()
把它展开,就得到,

这就是圆周率的由来。
有了这些认识,就不难理解一些问题,比如圆周率的超越性。它的结构要求它,显然是不可能出现循环的。它的精度在于“项数改成无限”的那一步,求和上限的虚数单位实际上就是求和的项数。或者说将这个四分之一圆周划分的份数,或者楼梯的阶数。随着这个阶数的增长,整个圆周的划分就越来越细。
现在让我们看看圆周率的精度和划分次数的关系,比如


如果我们发现某个圆周率的数值
![]()
那么,我们就可以说,在这个系统里面,
![]()
![]()
当然现实的情况中虚数单位不会这么小。但这给了我们一个获取本地空间虚数单位大小的方式。比如我们知道光速是一种虚数单位,它的物理数值为299792458m/s,但我们不知道米和秒之间的关系。如果我们能通过测量圆周率知道这个虚数单位的数学数值,我们就能得知米和秒之间的具体对应,就可以把米和秒彻底统一起来了。
为了说清上述圆柱到底是什么样子的,让我们求它的“体积”也就是总量。
我们知道半径,
![]()
也就是旋转楼梯的每一个台阶的长是10个单位。然后分为四个阶段,第一个阶段(第一象限)的总数,
![]()
第二个阶段(第二象限),
![]()
第三个阶段(第三象限),
![]()
第四个阶段(第四象限),
![]()
总量,
![]()
可见
这是一个极大的数字,而这只是第一个周期而已。