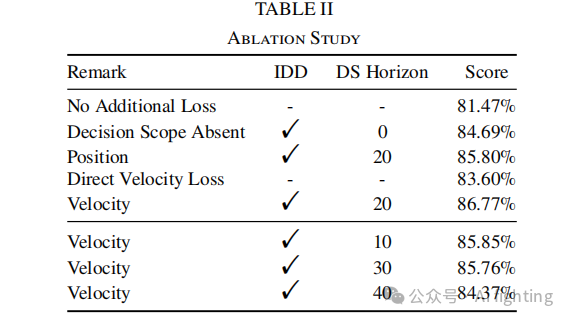
教程中H矩阵写的有问题，上图中H矩阵应该是（n+1) x (m+1)

                 共点不变性,下图中黄色方块标记的点，在射影变换前后，虽然直线的形状有所变化，但仍然相交于同一个点。

                共线不变性，下图黄色标记的两个点，在射影变换前后，仍然在同一条直线上。

                 交比看下图，中心点为S，发出四条射线（绿色），蓝色直线与这四条射线相交于A,B,C,D四个交点，交比定义为AB*CD/BC*AD。

        关于交比的详细说明，可参考如下链接：

【几米说平面几何】几何进阶知识（一）交比 - 哔哩哔哩交比，是一个对绝大多数读者比较陌生的话题。但它是属于射影几何的重要内容。大家可能会纳闷，up你不是研究竞赛几何的吗？为什么会讲这个比较进阶的知识呢？其实我们在初等几何的研究上，只会用到这个庞大体系的冰山一角，而且不甚严谨。但是这个知识作为一个研究问题的工具，如果掌握得当，会让你对很多问题有新的观点和思路。比如调和点列，完全四边形，笛沙格定理等等。本知识就好似SOS技术之于不等式，升幂定理之于数论，虽然重要，但不必要。如果大家比较功利只是为了考联赛的话，请跳过本文的阅读，避免带来无意义的时间浪费！https://www.bilibili.com/read/cv13253421/         

          对于齐次坐标理解，可以参考下图，可以知道W=1时，相当于X点所在的平面抬升到了垂直高度为1的位置，对于无穷远的点，W=0， 因此无穷远的点相当于这个平面回到了原点高度位置。

         

        平面和点的表示实际都是一个4维向量（齐次）

     

 

 

        上图对比了射影变换和仿射变换的区别，对于射影变换，平行四边形变换后平行的线关系会变化，而仿射变换不会改变平行关系。

        上图中是矫正矩阵，可以将射影变换结果矫正为仿射变换的结果，可以理解为把平行关系恢复。 

        如上图，假设相机拍摄到的画面是左下角的图像，我们可以通过找到射影变换空间里的两条平行线l1,l2得到射影空间下两条直线的交点v1(通过叉积),同理可得到l3,l4的交点v2。连接V1,V2可得到对应的无穷远的直线。找到这条无穷远直线后，我们就能得到矫正矩阵，这样就能将射影变换空间的坐标转换到仿射变换空间的坐标中。

        下图总结了2D和3D变换中的各种变换的自由度