要往前走,就得先忘掉过去。
—《阿甘正传》

🏰代码及环境配置:请参考 环境配置和代码运行!
确定性采样运动规划是一种采用确定性采样策略进行运动规划的方法。它通过按照预定规则生成采样点来构建解空间,并用于后续的路径搜索或优化过程。这种方法具有确定性和可重复性、高效性和适应性等优势,但也面临采样策略设计、高维空间问题和计算复杂度等挑战。其主要分为基于控制空间的采样和基于状态空间的采样,接下来将分别介绍这两种采样方式。

基于控制空间(control space)的采样是运动规划中的一种重要方法,它侧重于在控制量的空间内进行采样,以生成可能的控制输入,进而通过这些控制输入来规划出运动轨迹。这种方法特别适用于需要考虑车辆或机器人动力学/运动学约束的情况。
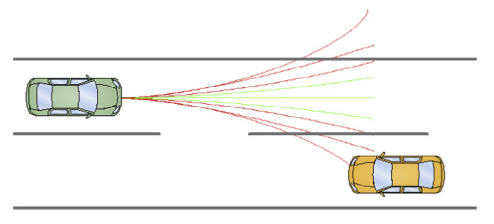
假设一个机器人运动的状态方程为 s ˙ = f ( s , u ) \dot{s}=f(s, u) s˙=f(s,u),其中 s s s表示所有可能的状态,例如位置信息 x x x, y y y,速度信息 x ˙ \dot{x} x˙, y ˙ \dot{y} y˙等, u u u表示控制输入。如下图所示:当前状态为 s 0 s_{0} s0,在采取不同的控制输入 u 0 , u 1 , u 2 u_{0} ,u_{1},u_{2} u0,u1,u2时,可以产生不同的终点状态 s f 0 , s f 1 , s f 2 s_{f}^{0} ,s_{f}^{1} ,s_{f}^{2} sf0,sf1,sf2 和不同的运动轨迹 s 0 → s f 0 , s 0 → s f 1 , s 0 → s f 2 s_{0}\overset{}{\rightarrow} s_{f}^{0} ,s_{0}\overset{}{\rightarrow}s_{f}^{1} ,s_{0}\overset{}{\rightarrow}s_{f}^{2} s0→sf0,s0→sf1,s0→sf2 。

3.3.1 基本概念
- 控制空间:由车辆或机器人的控制量构成的空间(例如对于车辆而言,可以将方向盘转角速率和纵向加加速度作为控制变量)。在这个空间中,每一个点都代表了一组特定的控制输入。
- 采样策略:指在运动规划过程中,直接在控制空间内按照一定的规则或策略进行采样,生成一系列的控制输入组合。然后,通过车辆或机器人的动力学/运动学模型,将这些控制输入转化为相应的运动轨迹,并进行评估和优化。
- **车辆的动力学/运动学模型:**具体细节在1.1节中讲解,此处不再赘述
3.3.2 优缺点
- 优点
- 符合动力学/运动学约束:直接在控制空间内进行采样,能够确保生成的轨迹符合车辆或机器人的动力学/运动学约束。
- 灵活性:采样策略可以根据具体问题的需求进行调整和优化,提高算法的灵活性
- 缺点
- 计算复杂性:需要对每个采样的控制序列进行状态推演,可能导致高计算成本。
- 优化难度:在控制空间中进行优化可能比在状态空间中更复杂。
- 采样效率:需要有效的采样策略来确保搜索效率和解的质量。
3.3.3 应用实例
3.3.3.1 无人机
- 若将无人机的状态为三维位置( x , y , z x, y, z x,y,z)和三维速度( x ˙ , y ˙ , z ˙ \dot{x}, \dot{y}, \dot{z} x˙,y˙,z˙),控制输入为三维加速度( x ¨ , y ¨ , z ¨ \ddot{x},\ddot{y},\ddot{z} x¨,y¨,z¨),并以此构建状态方程 s ˙ = A ⋅ s + B ⋅ u \dot{s} = A\cdot s + B\cdot u s˙=A⋅s+B⋅u,采用不同的控制输入,采样出来的轨迹如下图所示:
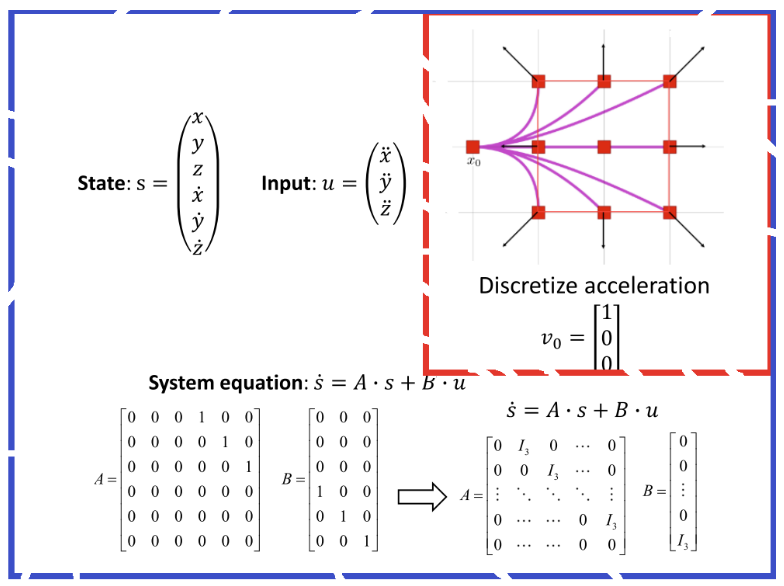
- 若将状态为三维位置( x , y , z x, y, z x,y,z)、三维速度( x ˙ , y ˙ , z ˙ \dot{x}, \dot{y}, \dot{z} x˙,y˙,z˙),三维加速度( x ¨ , y ¨ , z ¨ \ddot{x},\ddot{y},\ddot{z} x¨,y¨,z¨),输入选为三维 j e r k jerk jerk,则采用不同的控制输入,采样出来的轨迹如下图所示:
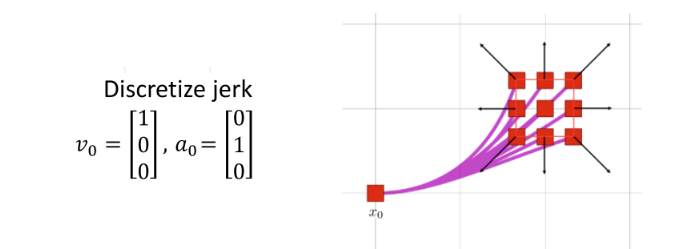
3.3.3.1 自动驾驶车辆
以自动驾驶车辆为例,一般情况下使用1.1节中的运动状态方程即可。此处的状态空间相比于1.1节中有更丰富的信息,不详细介绍,仅仅列出相应的公式,有兴趣者可自行研究。
状态空间为:
$\left [ x, y, theta,\delta, v, a \right ] ^{T}$
控制量为:
[ ω , j e r k ] T [ \omega , jerk] ^{T} [ω,jerk]T
状态转移模型为:
x ˙ = v cos θ y ˙ = v sin θ θ ˙ = v tan δ L δ ˙ = ω v ˙ = a a ˙ = j \begin{array}{l}\dot{x}=v \cos \theta \\\dot{y}=v \sin \theta \\\dot{\theta}=\frac{v \tan \delta }{L} \\\dot{\delta}=\omega \\\dot{v}=a \\\dot{a}=j\end{array} x˙=vcosθy˙=vsinθθ˙=Lvtanδδ˙=ωv˙=aa˙=j
并且基于状态量,我们可以基于以下公式得到kappa和dkappa:
k a p p a = tan δ L d k a p p a = d k d s = d k d t d t d s = ω L v cos δ cos δ \begin{align*} kappa &= \frac{\tan \delta }{L} \\dkappa &= \frac{dk}{ds} =\frac{dk}{dt}\frac{dt}{ds}=\frac{\omega }{Lv\cos \delta \cos \delta} \end{align*} kappadkappa=Ltanδ=dsdk=dtdkdsdt=Lvcosδcosδω
其中: ( x , y ) \left ( x, \ y \right ) (x, y) 是车辆的位置, θ \theta θ 是车辆的航向角(横摆角), ϕ \phi ϕ 是前轮转角, δ \delta δ 是前轮转角, ω \omega ω 前轮转角速度, L L L是车辆轴距, v v v是车辆速度, a a a是车辆加速度, j j j是车辆加加速度。
本节提供了基于控制空间采样的代码测试,其中代码是以1.1节中的自行车模型为基础进行实现的:
python3 tests/sampling_based_planning/control_based_sampler_test.py
3.3.c.1 基于控制空间采样的代码实现
在tests/sampling_based_planning/control_based_sampler_test.py 中定义了轨迹的生成方式,其中:
start_p :轨迹的起点
v :车辆的驾驶速度,在每一阶段,按照匀速行驶
max_steer :车辆最大的前轮转角
min_steer :车辆最小的前轮转角
delta_steer :方向盘转角的分辨率
delta_t:生成轨迹点的时间分辨率
total_t:轨迹的总时长
def generate_trajectories(
start_p, v, min_steer, max_steer, delta_steer, delta_t, total_t
):
trajectories = []
for steer in np.arange(min_steer, max_steer + delta_steer, delta_steer):
points = [start_p]
points[-1].steer = steer
for t in np.arange(0, total_t, delta_t):
new_p = bicycle_model(points[-1], v * delta_t)
points.append(new_p)
trajectories.append(points)
return trajectories
3.3.c.2 基于控制空间采样的代码测试
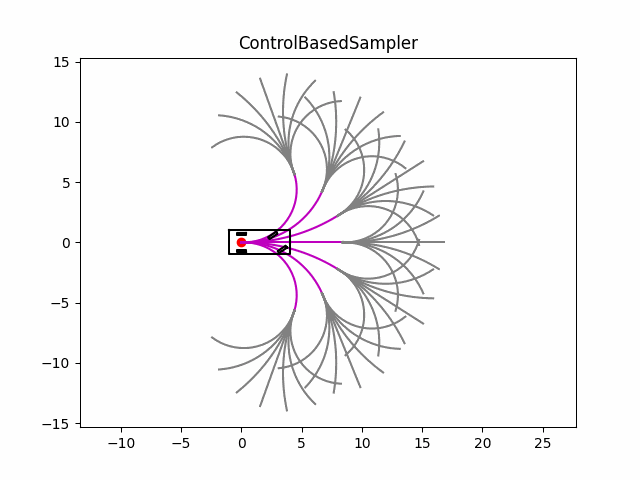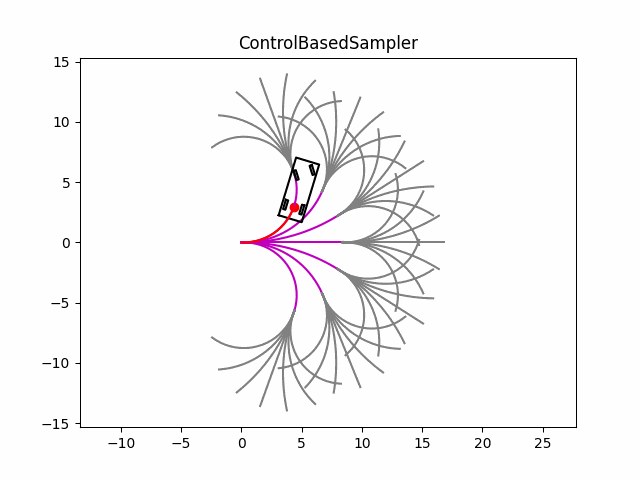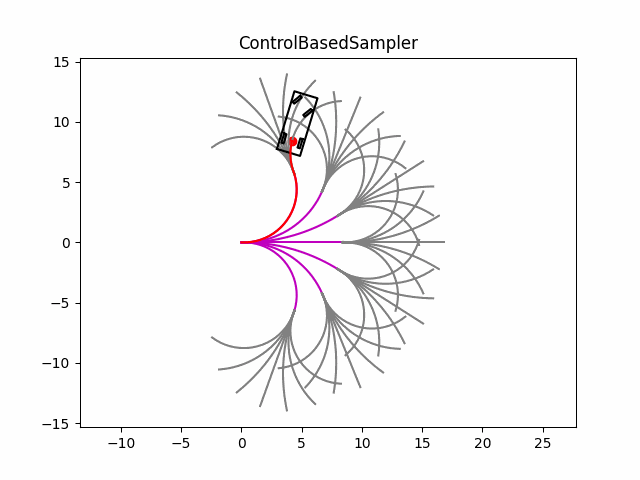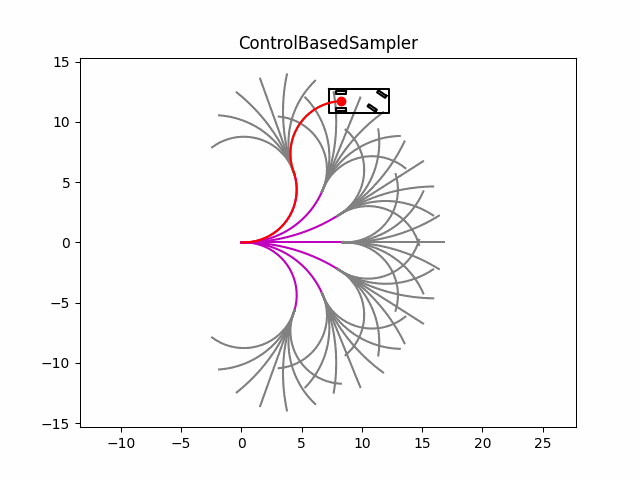
在测试中,分为两个阶段,第一个阶段从起始点开始,按照不同的前轮转角往前推出行驶轨迹(效果图中的洋红色曲线),第二阶段,以第一阶段轨迹的最后一个点为起点,然后继续按照不同的前轮转角往前推出行驶轨迹(效果图中的灰色曲线);然后设置不同的cost来评估每一条曲线,最后基于cost选出最优轨迹(为了测试,代码中的cost没有填充,只是随机选择了一条轨迹,效果图中的红色曲线)。
从效果图也可以看出,基于控制空间的采样方式可以生成满足运动学约束的曲线,但由于没有其他约束,会导致生成需要无用的轨迹(例如超出道路边界等)。
def plot_trajectories(trajectories, color="m"):
for points in trajectories:
plt.plot([p.x for p in points], [p.y for p in points], color=color)
def select_optimal_path(paths, random_select=True):
if random_select:
return paths[np.random.randint(len(paths))]
# 这里可以添加更复杂的评估逻辑来选择最佳路径
return None
def main():
start_p = Point()
start_p.theta = 0.0
start_p.v = 4.0
max_steer = 0.6
min_steer = -0.6
delta_steer = 0.2
delta_t = 0.1
total_t = 2.0
# First phase.
fig = plt.figure()
first_phase_trajectories = generate_trajectories(
start_p, start_p.v, min_steer, max_steer, delta_steer, delta_t, total_t
)
plot_trajectories(first_phase_trajectories)
# Second phase.
second_phase_paths = []
for curve in first_phase_trajectories:
second_phase_trajectories = generate_trajectories(
curve[-1], curve[-1].v, min_steer, max_steer, delta_steer, delta_t, total_t
)
plot_trajectories(second_phase_trajectories, color="grey")
for path in second_phase_trajectories:
# Connect the trajectories of first phase and second phase.
path = curve[:-1] + path
second_phase_paths.append(path)
# Select a optimal path: we can set many cost to evaluate the path, such as:
# 1. Distance cost.
# 2. Speed cost.
# 3. Steer cost.
# 4. Acceleration cost.
# 5. Jerk cost.
# ...
# Here, we randomly select a path from the curve_list.
selected_curve = select_optimal_path(second_phase_paths)
plt.title("ControlBasedSampler")
animation_car(
fig,
selected_curve,
save_path=get_gif_path(
pathlib.Path(__file__), str(pathlib.Path(__file__).stem)
),
)
if __name__ == "__main__":
main()
🏎️自动驾驶小白说官网:https://www.helloxiaobai.cn














![微信小程序,打开新的项目,调试遇见[ app.json 文件内容错误] app.json: 在项目根目录未找到 app.json](https://i-blog.csdnimg.cn/direct/cdfd4adcb92e440f9bfcc24f4f347958.png)




