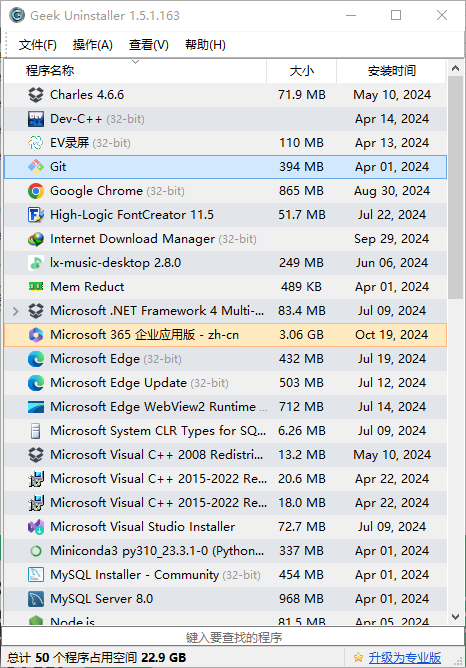
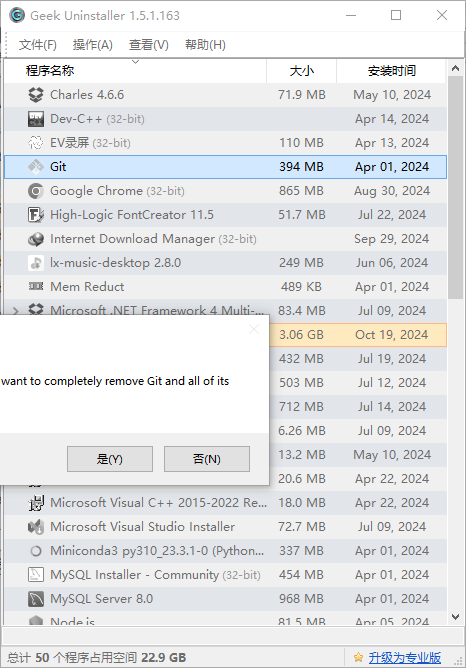
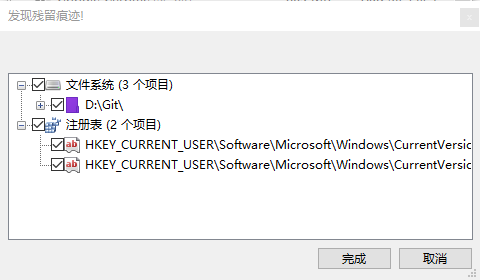
卸载 Git

news2024/11/28 6:38:57

打开 Geek

在这里插入图片描述

找到 Git

在这里插入图片描述

右键卸载 Git

在这里插入图片描述

卸载完成

在这里插入图片描述

等待扫描注册表

在这里插入图片描述

点击完成

在这里插入图片描述
已经删除完毕

清除Git在本地的配置文件

进入 C:\Users\用户名
在这里插入图片描述
删除框起来的配置文件

👇 源码资料获取 · 技术与交流 👇

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2219091.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

【移动安全】OWASP MASTG 移动应用程序安全测试指南

OWASP 是 Open Web Application Security Project MASTG 是 Mobile Application Security Testing Guide 移动应用程序安全测试指南英文网站：https://mas.owasp.org/MASTG/ 中文网站：http://www.owasp.org.cn/OWASP-CHINA/owasp-project/owasp-mobile-…

Docker本地镜像发布到Docker Registry私有仓库

1. 私有仓库私有库可以部署在本地或私有云环境中，我们可以控制镜像的访问权限。相比公共仓库，私有库提供了更高的安全性和更快的访问速度。此外，私有库还支持自定义，你可以根据自己的需求来配置仓库。私有仓库解决方案 Harbo…

递归神经网络解释(RNN)

Recurrent Neural Network (RNN) 如今，不同的机器学习技术用于处理不同类型的数据。最难处理和预测的数据类型之一是顺序数据。顺序数据与其他类型的数据不同，因为虽然可以假设典型数据集的所有特征都是与顺序无关的，但不能假设顺序数据集是无关的。为了处理这种类型的数据…

018_基于python+django荣誉证书管理系统2024_jytq9489

目录系统展示开发背景代码实现项目案例获取源码博主介绍：CodeMentor毕业设计领航者、全网关注者30W群落，InfoQ特邀专栏作家、技术博客领航者、InfoQ新星培育计划导师、Web开发领域杰出贡献者，博客领航之星、开发者头条/腾讯云/AW…

【服务器部署】Docker部署小程序

一、下载Docker 安装之前，一定查看是否安装docker，如果有，卸载老版本我是虚拟机装的Centos7，linux 3.10 内核，docker官方说至少3.8以上，建议3.10以上（ubuntu下要linux内核3.8以上&#xff0c…

如何修改网络ip地址：一步步指南‌

在当今这个数字化时代，网络已成为我们日常生活与工作中不可或缺的一部分。无论是浏览网页、在线办公还是享受流媒体服务，稳定的网络连接和适当的IP地址管理都是确保良好体验的关键。然而，出于隐私保护、绕过地理限制或测试网络环境等需要&…

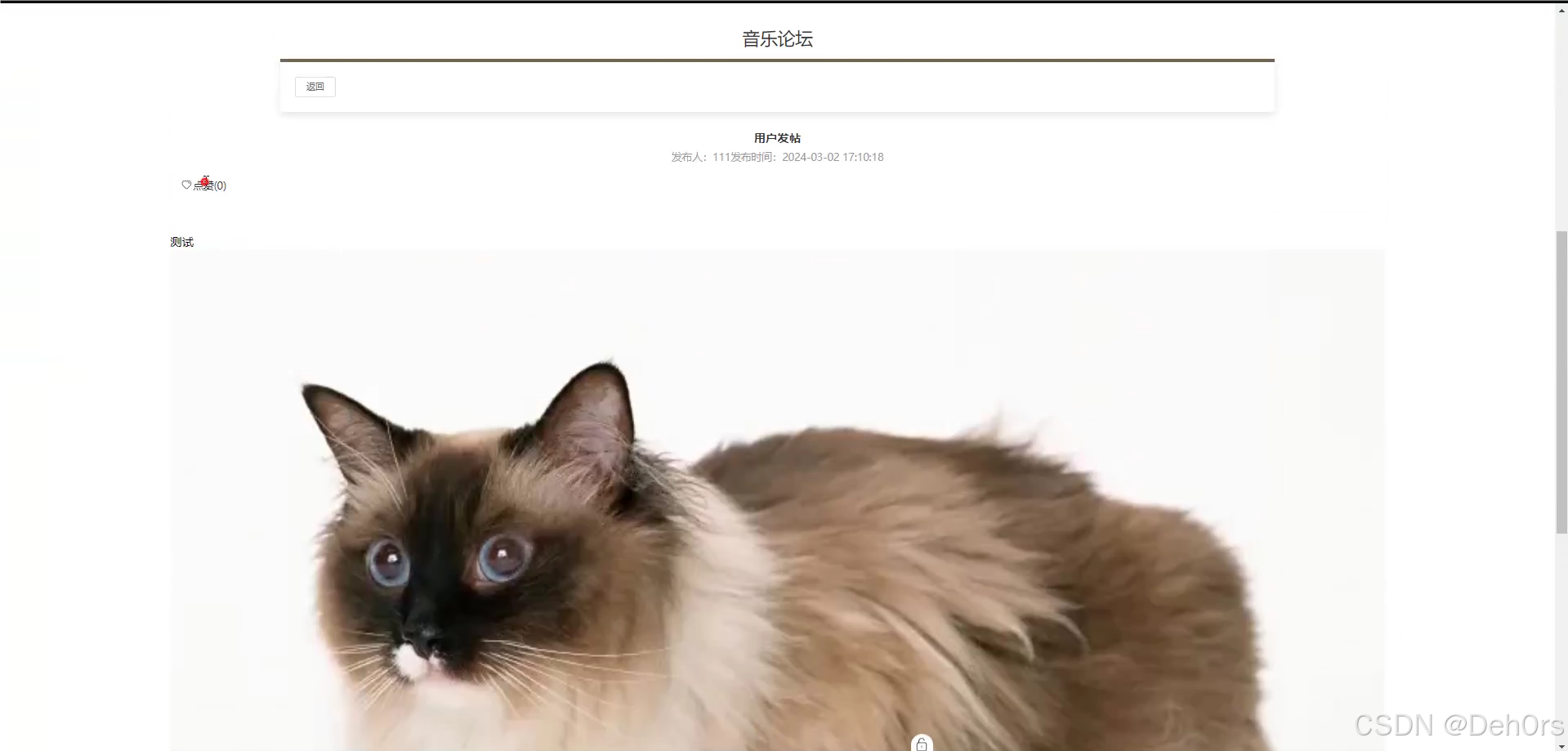
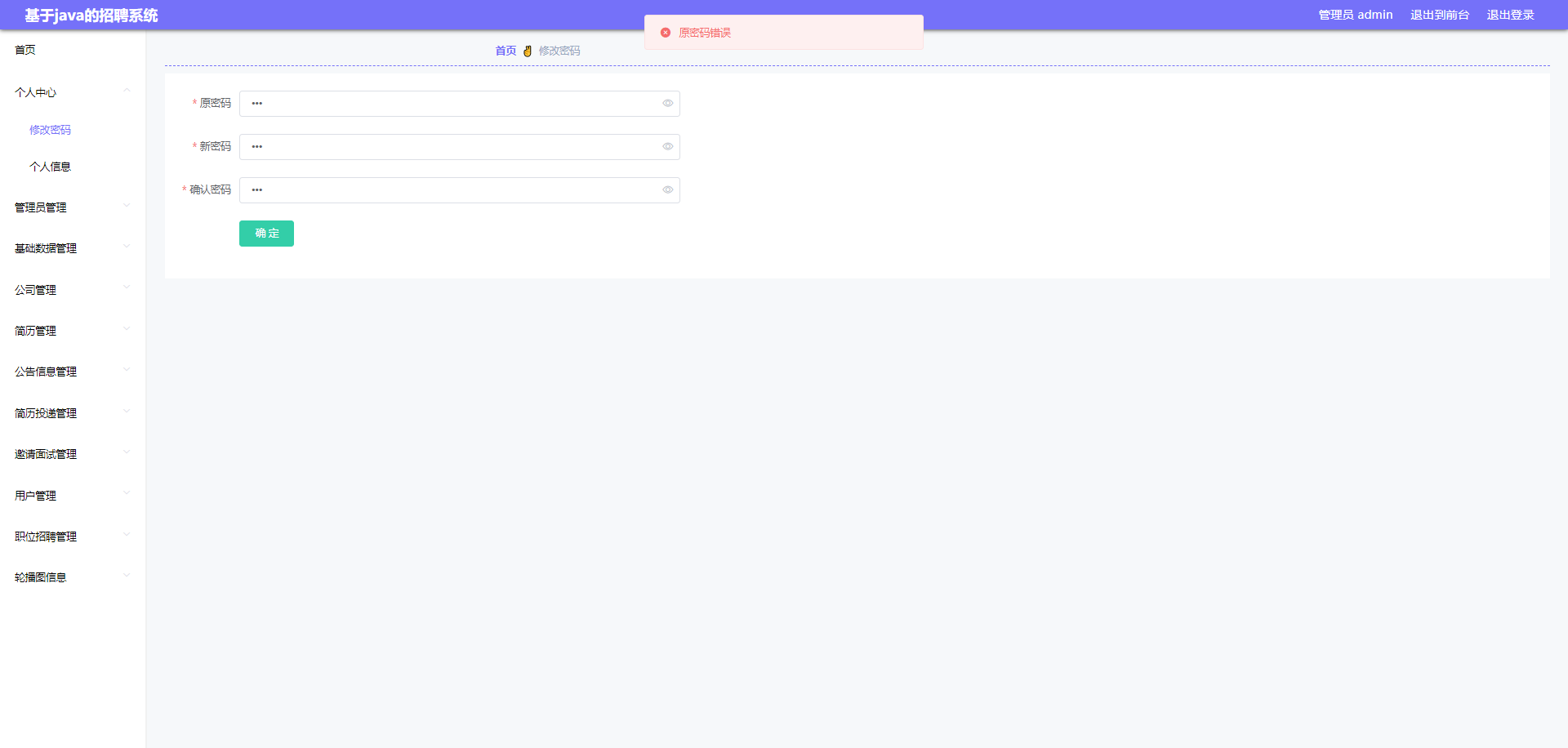
ssm基于java的招聘系统设计与开发+vue

系统包含：源码论文所用技术：SpringBootVueSSMMybatisMysql 免费提供给大家参考或者学习，获取源码请私聊我需要定制请私聊目录第1章绪论 1 1.1 课题背景 1 1.2 课题意义 1 1.3 研究内容 1 第2章开发环境与技术 3 2.1 Java语言…

Java | Leetcode Java题解之第495题提莫攻击

题目： 题解： class Solution {public int findPoisonedDuration(int[] timeSeries, int duration) {int ans 0;int expired 0;for (int i 0; i < timeSeries.length; i) {if (timeSeries[i] > expired) {ans duration;} else {ans timeSerie…

2011年国赛高教杯数学建模B题交巡警服务平台的设置与调度解题全过程文档及程序

2011年国赛高教杯数学建模 B题交巡警服务平台的设置与调度有困难找警察”，是家喻户晓的一句流行语。警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。为了更有效地贯彻实施这些职能，需要在市区的一些交通要道和重要部位设置交巡警服务平台…

【PFGA】二选一数选器

文章目录前言一、实验原理二、实验过程三、实验结果参考文献前言进行 verilog FPGA 实验一、实验原理二、实验过程三、实验结果代码 module mux21(input s,input a,input b,output reg y); always(s or a or b) beginif (~s) beginy<a;end else beginy<…

触想工业一体机赋能BMS楼宇管理，让建筑活起来

一、行业发展背景城市化进程的飞速发展，持续刷新着人们对于现代建筑在舒适度、节能安全、自动化方面的期待。在此趋势下，诸如暖通空调、用电照明、门禁消防等建筑配套子系统不断扩充完善，建筑物从简单的物理结构膨胀为庞大的楼宇生态系统&am…

go jwt 用户登录和返回用户信息 token ----important!!!

1.每一行代码都有详细注释，解释了其功能和作用。这些注释可以帮助你理解代码如何工作，特别是在处理用户登录、生成 JWT、验证 JWT 和返回用户信息的过程中。 package main // 指定这个文件是一个可执行程序import ("fmt" …

深度学习面经总结

人不走空 🌈个人主页：人不走空 💖系列专栏：算法专题 ⏰诗词歌赋：斯是陋室，惟吾德馨目录 🌈个人主页：人不走空 💖系列专栏：算法专题 ⏰诗词歌…

【动态规划数学归纳法二项式定理】C++ 算法458:可怜的小猪

作者推荐视频算法专题本文涉及知识点数学归纳法二项式定理动态规划汇总数学力扣458:可怜的小猪有 buckets 桶液体，其中正好有一桶含有毒药，其余装的都是水。它们从外观看起来都一样。为了弄清楚哪只水桶含有毒药，你可以喂一些…

linux线程 | 全面理解同步与互斥 | 同步

前言：本节内容主要讲解linux下的同步问题。同步问题是保证数据安全的情况下，让我们的线程访问具有一定的顺序性。线程安全就规定了它必须是在加锁的场景下的！！那么， 具体什么是同步问题， 我们加下来看看吧…

基于Matlab车牌识别课程设计报告模板(附源代码)

目录一．课程设计目的……………………………………………3 二．设计原理…………………………………………………3 三．详细设计步骤……………………………………………3 四. 设计结果及分析…………………………………………18 五. …

NC 单据模板自定义项设置参照（自定义参照）

NC 单据模板自定义项设置参照（自定义参照） 如图下图，NC 单据模板自定义项设置参照： 1、选择需要设置参照的自定义字段，选择高级属性页签，在类型设置中，数据类型选择参照信息，即bd…

DART: Implicit Doppler Tomography for Radar Novel View Synthesis 笔记

Link：https://wiselabcmu.github.io/dart/ Publish： 2024CVPR Abstract DART主要任务就是用来合成雷达距离多普勒图像range-droppler，可用于生成高质量的断层扫描图像。 Related Work 1 Radar Simulation 基于模型的方法任务&#xff…