
摘要
本文提出了一种基于环形拓扑的多目标粒子群优化算法 (MO-Ring-PSO-SCD) 用于解决无人机的三维路径规划问题。该算法同时优化了无人机路径的路径成本和威胁成本,通过粒子群算法的多目标优化能力实现路径选择。实验结果表明,与传统算法相比,该方法能够有效平衡路径长度和安全性,为无人机的实际应用提供了理论和实践支持。
理论
-
MO-Ring-PSO-SCD算法: 该算法基于环形拓扑结构设计,确保粒子之间的通信以环形方式进行,从而避免了全连接网络中的通信瓶颈问题。粒子群通过自适应学习和多目标优化来进行路径规划,两个目标分别是路径成本最小化和威胁成本最小化。
-
路径成本与威胁成本: 路径成本由无人机飞行路径的长度决定,威胁成本则由路径经过的区域威胁等级决定。算法中通过定义适应度函数,将两个目标结合以实现优化。
实验结果
-
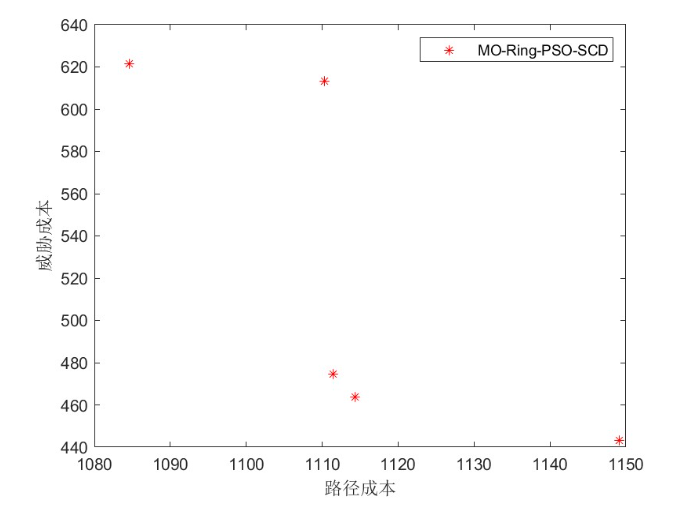
图1: 显示了多次优化后的无人机路径成本与威胁成本的散点分布情况。每个点代表一次优化结果,显示了不同权衡下的优化结果。
-
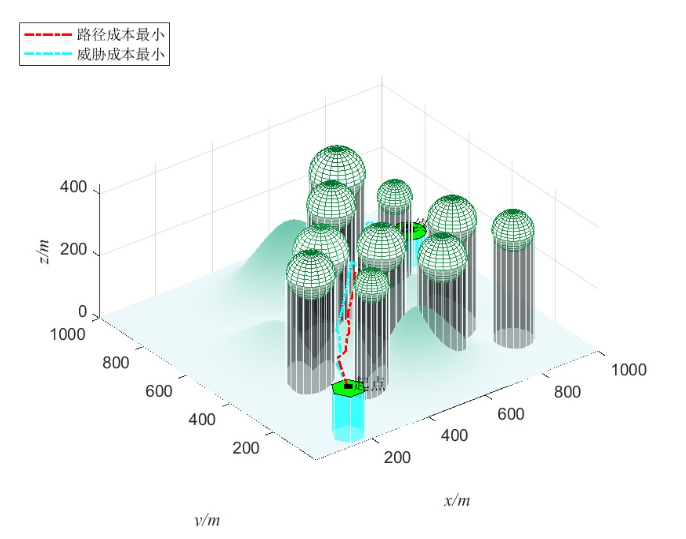
图2和图3: 展示了无人机在三维空间中的路径规划。红色虚线代表路径成本最小化的路径,蓝色虚线代表威胁成本最小化的路径。从实验结果来看,MO-Ring-PSO-SCD能够在多维目标下优化路径选择,找到兼顾路径长度与威胁规避的最优解。

部分代码
% 粒子群参数设置
num_particles = 30;
num_iterations = 100;
w = 0.729; % 惯性权重
c1 = 1.49445; % 认知加速度系数
c2 = 1.49445; % 社会加速度系数
% 初始化粒子位置与速度
positions = rand(num_particles, 3); % 初始化粒子的位置 (x, y, z)
velocities = zeros(num_particles, 3); % 初始化速度
% 优化过程
for iter = 1:num_iterations
for i = 1:num_particles
% 计算路径成本与威胁成本
path_cost = calculatePathCost(positions(i, :));
threat_cost = calculateThreatCost(positions(i, :));
% 更新速度和位置
velocities(i, :) = w * velocities(i, :) + ...
c1 * rand() * (pbest(i, :) - positions(i, :)) + ...
c2 * rand() * (gbest - positions(i, :));
positions(i, :) = positions(i, :) + velocities(i, :);
end
end
% 成本计算函数
function cost = calculatePathCost(position)
% 计算路径长度或其他相关成本
cost = norm(position);
end
function cost = calculateThreatCost(position)
% 根据位置计算威胁值
cost = threatMap(position(1), position(2), position(3));
end
参考文献
❝
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942-1948.
Clerc, M., & Kennedy, J. (2002). The particle swarm - Explosion, stability, and convergence in a multidimensional complex space. IEEE Transactions on Evolutionary Computation, 6(1), 58-73.
Zhang, Q., & Li, H. (2007). MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 11(6), 712-731.
(文章内容仅供参考,具体效果以图片为准)



















