🌈个人主页：秋风起，再归来~
🔥系列专栏：C++刷题算法总结
🔖克心守己，律己则安
目录
前言：双指针
1. 移动零（easy）
2. 复写零（easy）
3. 快乐数（medium）
4. 盛⽔最多的容器（medium）
5. 完结散花
前言：双指针
常⻅的双指针有两种形式，⼀种是对撞指针，⼀种是左右指针。
对撞指针：⼀般⽤于顺序结构中，也称左右指针。
• 对撞指针从两端向中间移动。⼀个指针从最左端开始，另⼀个从最右端开始，然后逐渐往中间逼 近。
• 对撞指针的终⽌条件⼀般是两个指针相遇或者错开（也可能在循环内部找到结果直接跳出循 环），也就是：
◦ left == right （两个指针指向同⼀个位置）
◦ left > right （两个指针错开）
快慢指针：⼜称为⻳兔赛跑算法，其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列 结构上移动。
这种⽅法对于处理环形链表或数组⾮常有⽤。
其实不单单是环形链表或者是数组，如果我们要研究的问题出现循环往复的情况时，均可考虑使⽤快 慢指针的思想。 快慢指针的实现⽅式有很多种，
最常⽤的⼀种就是：
• 在⼀次循环中，每次让慢的指针向后移动⼀位，⽽快的指针往后移动两位，实现⼀快⼀慢。
1. 移动零（easy）
「数组分两块」是⾮常常⻅的⼀种题型，主要就是根据⼀种划分⽅式，将数组的内容分成左右两部 分。这种类型的题，⼀般就是使⽤「双指针」来解决。
题目链接
https://leetcode.cn/problems/move-zeroes/
给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
请注意 ，必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:输入: nums = [0]
输出: [0]
进阶：你能尽量减少完成的操作次数吗？
解题思路：
1、我们先定义两个指针cur和pre。
2、我们用cur来扫描整个数组。
a、如果cur位置为0，我们不进行处理，cur++。
b、如果cur位置不为0，我们让cur位置和pre位置的元素交换，pre++，cur++。
3、通过以上的操作，我们把该数组进行了区域划分：[0,pre)区域的元素是非零的，[pre,cur)区域的元素是0，而[cur,len)区域是没有判断的区域。
4、循环以上的操作，当cur走到数组末尾时，结束循环。
具象图
抽象图
解题代码：
class Solution {
public:
void moveZeroes(vector<int>& nums)
{
int len=nums.size();
for(int cur=0,pre=0;cur<len;cur++)
{
if(nums[cur]!=0) swap(nums[cur],nums[pre++]);
}
}
};2. 复写零（easy）
题目链接https://leetcode.cn/problems/duplicate-zeros/description/
给你一个长度固定的整数数组 arr ，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。
注意：请不要在超过该数组长度的位置写入元素。请对输入的数组 就地 进行上述修改，不要从函数返回任何东西。
示例 1：
输入：arr = [1,0,2,3,0,4,5,0]
输出：[1,0,0,2,3,0,0,4]
解释：调用函数后，输入的数组将被修改为：[1,0,0,2,3,0,0,4]
示例 2：输入：arr = [1,2,3]
输出：[1,2,3]
解释：调用函数后，输入的数组将被修改为：[1,2,3]
解题思路：
1、我们先定义两个指针cur=-1,des=1。
2、cur扫描数组：
a、cur位置为0，des走两步
b、cur位置不为0，des走一步
3、当des大于等于len-1位置时结束循环
4、cur的作用是走到最终被重写的元素，而des的作用是找到我们从后往前复写开始的位置
5、如果我们从前往后复写的话，有可能会把我们需要复写的元素覆盖！
int cur = -1;
int des = -1;
int len = arr.size();
while (des < len-1)
{
cur++;
if (arr[cur] == 0)
des += 2;
else
des++;
}6、处理边界情况，如果最后一个要复写的元素是0，那么des的位置会走到len（即数组的长度不够我们复写两个0），这时我们要单独处理这种情况，提前复写一个0即可。
if (des == len)
{
cur--;
arr[des - 1] = 0;
des -= 2;
}7、从前往后复写
while (cur >= 0)
{
if (arr[cur] == 0)
{
arr[des--] = 0;
arr[des--] = 0;
}
else arr[des--] = arr[cur];
cur--;
}解题代码：
class Solution
{
public:
void duplicateZeros(vector<int>& arr)
{
int cur = -1;
int des = -1;
int len = arr.size();
//找到最后一个数
while (des < len-1)
{
cur++;
if (arr[cur] == 0)
des += 2;
else
des++;
}
//处理边界情况
if (des == len)
{
cur--;
arr[des - 1] = 0;
des -= 2;
}
//从后往前复写
while (cur >= 0)
{
if (arr[cur] == 0)
{
arr[des--] = 0;
arr[des--] = 0;
}
else arr[des--] = arr[cur];
cur--;
}
}
};3. 快乐数（medium）
题目链接https://leetcode.cn/problems/happy-number/description/
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为：
对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ；不是，则返回 false 。示例 1：
输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2：输入：n = 2
输出：false
解题思路：
1、通过分析以上两个例子，我们会发现当数字为快乐数时，它其实是在1当中死循环，当数字不是快乐数时，它其实是以自己初识位置为起点，但不能变化为一，最后进入一个死循环的过程。
2、而我们只要找到这个过程当中刚进入循环的数字是否为1即可判断该数字是否是快乐数。
3、我们可以快速的联想到链表当中的一个经典题型，这题也是如此，我们只要用快慢指针的思想就可以解决这个问题！
思考：为什么数字的变化一定只有这两种情况呢？
1、变为1后进入死循环。
2、最后没有变为1进入死循环。
还有一种情况：一直变化，不进入循环。（可能吗？）
题目说明了n的最大值是2^31-1即2,147,483,647。取最大值的每一位的平方和为260，所以n变化所得结果的范围在1~260之间。假设n从开始非常不幸经过了260次变化，恰好1~260之间的数字都变化得到过，那在261次变化时，其结果一定是1~260之间的某个元素，所以这个过程中一定会进入循环！（鸽巢原理）
4. 盛⽔最多的容器（medium）
题目链接https://leetcode.cn/problems/container-with-most-water/description/
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。
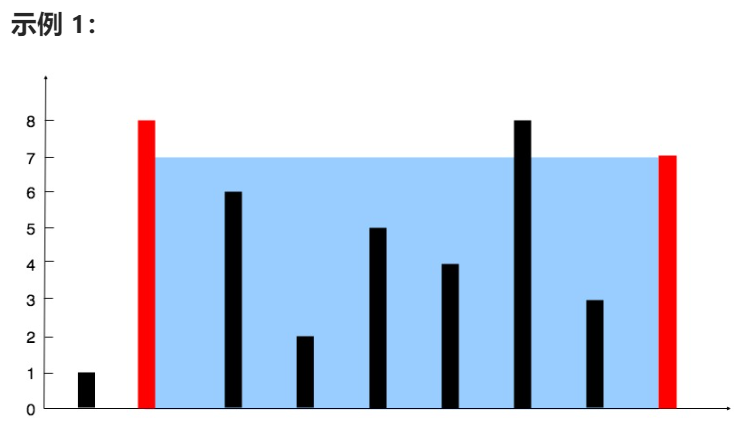
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
示例 2：输入：height = [1,1]
输出：1
解题思路：
1、暴力枚举：这种题目我们最先想到的就是暴力枚举所有的面积，然后不断更新结果，找到最大的面积即可。不过这种n^2的算法一般在leetcode中等题型上提交都会超出时间的限制。
class Solution {
public:
int maxArea(vector<int>& height) {
int len=height.size();
int ret=0;
for(int left=0;left<len-1;left++)
{
for(int right=1;right<len;right++)
{
int tmp=(right-left)*min(height[left],height[right]);
ret=max(tmp,ret);
}
}
return ret;
}
};
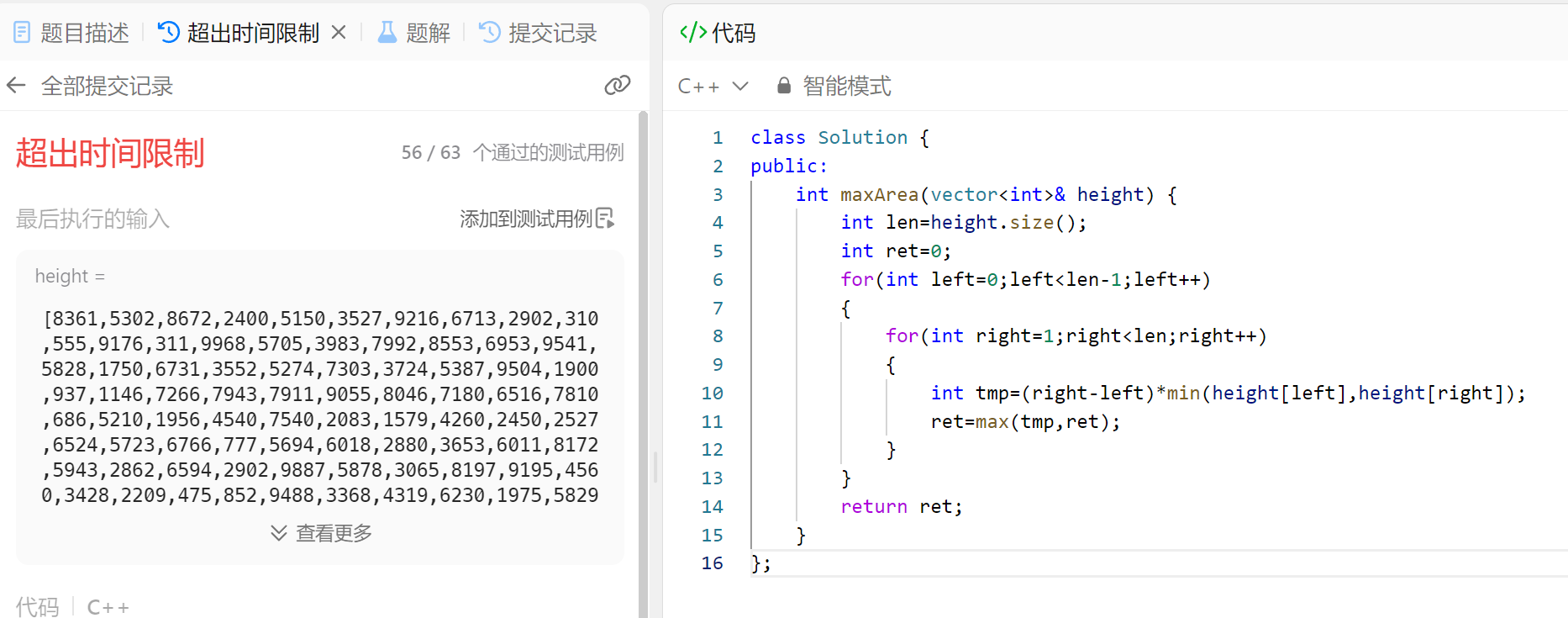
2、不过尽管如此，暴力解决问题的算法还是有其意义的，我们一般很难直接想到最优解法，所以我们可以在暴力解法的基础上去不断进行优化！
更优解法：
3、我可以定义left在数组的开头，right在数组的结尾。记录此时的面积，然后比较这两个位置的数值大小。
a.我们先固定数值较小（假设是left）的位置，然后移动数值较大（right）的一侧。这时我们会发现移动数值较大一侧元素时，枚举的所有情况的面积都是减小的！原因在于：首先宽是不断减小的，如果高right减小，总高度减小，如果增大，高度不变。这也就意味着固定left（较小一侧）位置所枚举的最大值就是当前位置，此时right就不再需要左移去，枚举其他情况（没有意义）！而此时固定较小端的所有情况就相当于枚举完了。
b.接着我们就让较小端的一侧++或--，循环知道left==right。此时所有情况都以枚举完成，我们只要将最大的结果记录下来就完了。
解题代码：
class Solution {
public:
int maxArea(vector<int>& height) {
int len=height.size();
int left=0,right=len-1,ret=0;
while(left<right)
{
//更新结果
int tmp=(right-left)*min(height[left],height[right]);
ret=max(ret,tmp);
//
if(height[left]<height[right]) left++;
else right--;
}
return ret;
}
};5. 完结散花
好了，这期的分享到这里就结束了~
如果这篇博客对你有帮助的话，可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话，可以点点关注，避免找不到我了呢~
我们下期不见不散~~
