在提供面经的同学中,竟然有同学在面试网易后台研发的时候遇到了一道困难难度的算法题。
一般来说,大多数面试的算法题都是以中等难度为主,遇到困难难度的算法题也许是公司现在不缺人、也许是在选拔人才、当然也很可能是面试官其实并不想要你。
但是不要灰心,虽然在网易的面试中遇到了困难题,但是还有那么多公司呢,总能遇到愿意发 offer 的。
今天带来和这位同学的网易面经中最相似的能找到的算法题:
题目描述:
题号:84
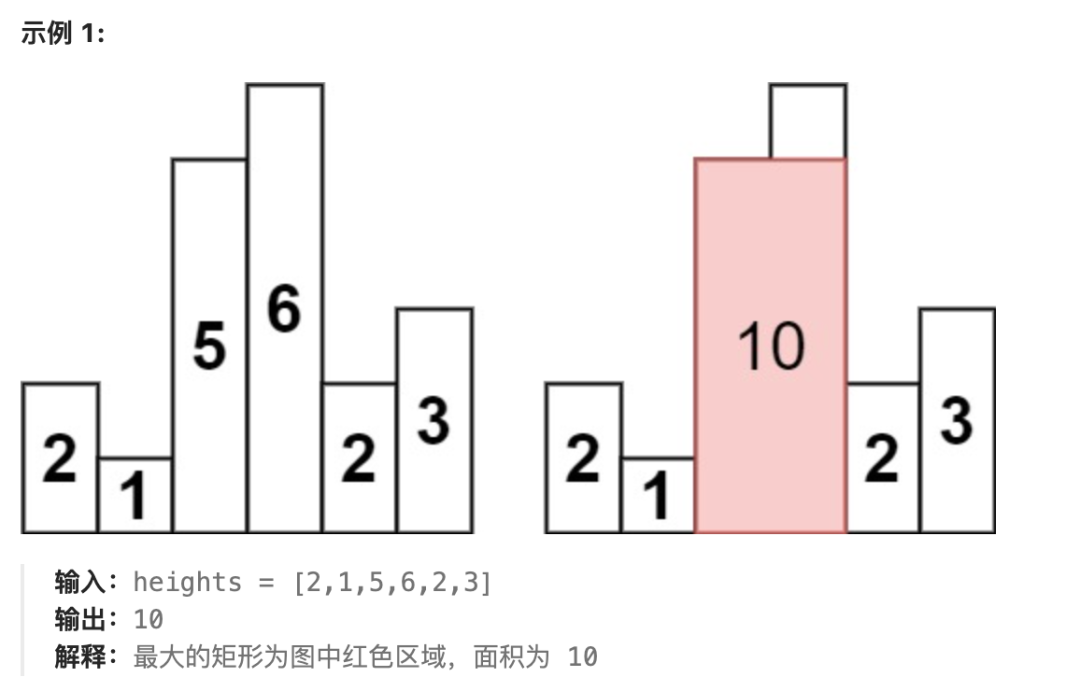
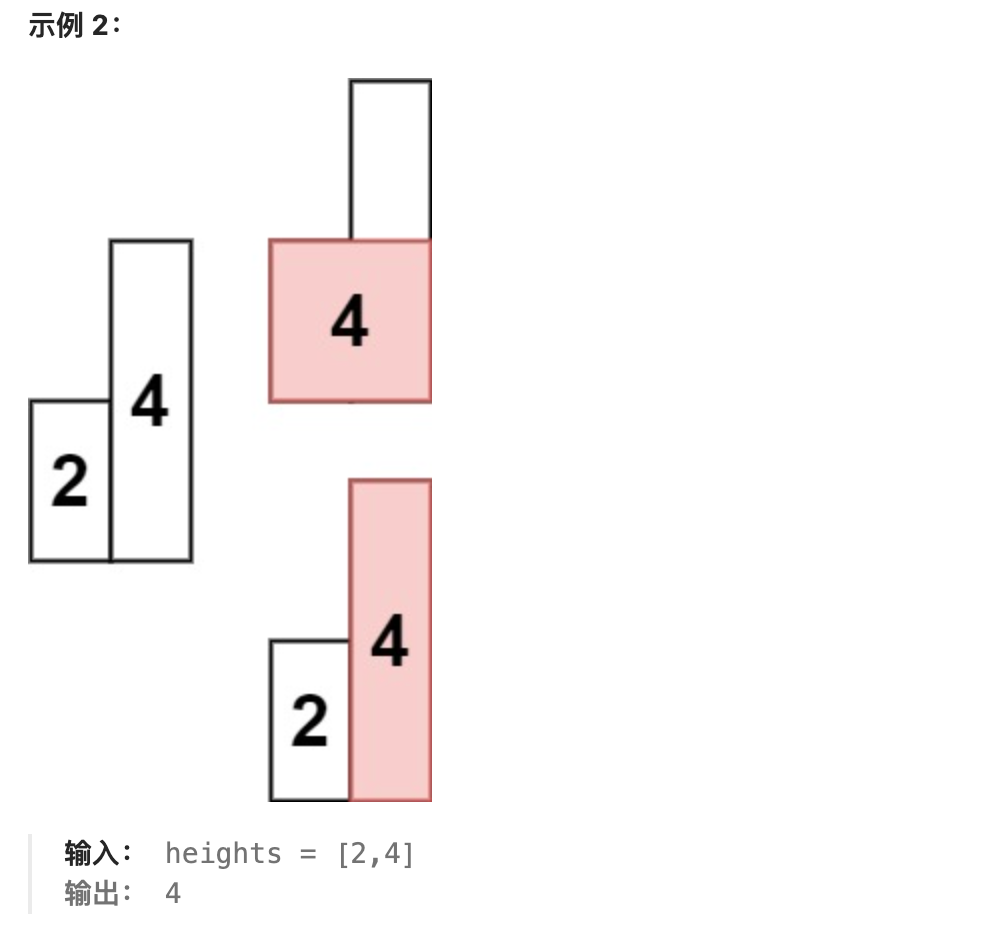
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
解题思路:
思路一:单调栈
在这个问题中,可以利用单调栈来找到每个柱子左边和右边第一个比它矮的柱子的位置,从而计算出以当前柱子高度为矩形高度的最大矩形面积。
具体步骤如下:
-
初始化一个空栈,以及一个用于存储每个柱子最大矩形面积的数组(初始化为0)。
-
从左到右遍历每个柱子:
-
如果栈为空或者当前柱子的高度大于栈顶柱子的高度,将当前柱子的索引压入栈中。
-
否则,弹出栈顶元素,并计算以该柱子高度为矩形高度的最大矩形面积(宽度为当前柱子索引与栈顶柱子索引之间的距离)。更新该柱子的最大矩形面积,并将该面积与之前的最大面积进行比较,取较大值作为当前的最大面积。重复此步骤直到栈为空或者当前柱子的高度大于栈顶柱子的高度,然后将当前柱子的索引压入栈中。
-
-
遍历结束后,栈中可能还剩余一些柱子。对于这些柱子,我们按照上述步骤计算以该柱子高度为矩形高度的最大矩形面积,并更新最大面积。
-
返回最大面积。
时间复杂度:O(n)
空间复杂度:O(n)
C++
// C++
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> stk;
int maxArea = 0;
heights.push_back(0); // 添加一个高度为0的柱子,以便将所有柱子弹出栈
for (int i = 0; i < heights.size(); ++i) {
// 弹出栈中所有高度大于当前柱子的柱子,并计算最大矩形面积
while (!stk.empty() && heights[i] < heights[stk.top()]) {
int h = heights[stk.top()];
stk.pop();
int w = i;
if (!stk.empty()) {
w = i - stk.top() - 1;
}
int area = h * w;
maxArea = max(maxArea, area);
}
stk.push(i);
}
return maxArea;
}
};go
// go
func largestRectangleArea(heights []int) int {
stack := []int{}
maxArea := 0
heights = append(heights, 0) // 添加一个高度为0的柱子,以便将所有柱子弹出栈
for i := 0; i < len(heights); i++ {
// 弹出栈中所有高度大于当前柱子的柱子,并计算最大矩形面积
for len(stack) > 0 && heights[i] < heights[stack[len(stack)-1]] {
h := heights[stack[len(stack)-1]]
stack = stack[:len(stack)-1]
w := i
if len(stack) > 0 {
w = i - stack[len(stack)-1] - 1
}
area := h * w
if area > maxArea {
maxArea = area
}
}
stack = append(stack, i)
}
return maxArea
}