多状态问题的核心就是每个位置不止有一个状态，因此需要多个dp表表示不同状态对应位置的值，然后根据题目考虑特定情况写出状态转移方程即可 

1.题目解析

题目来源：面试题17.16.按摩师——力扣 

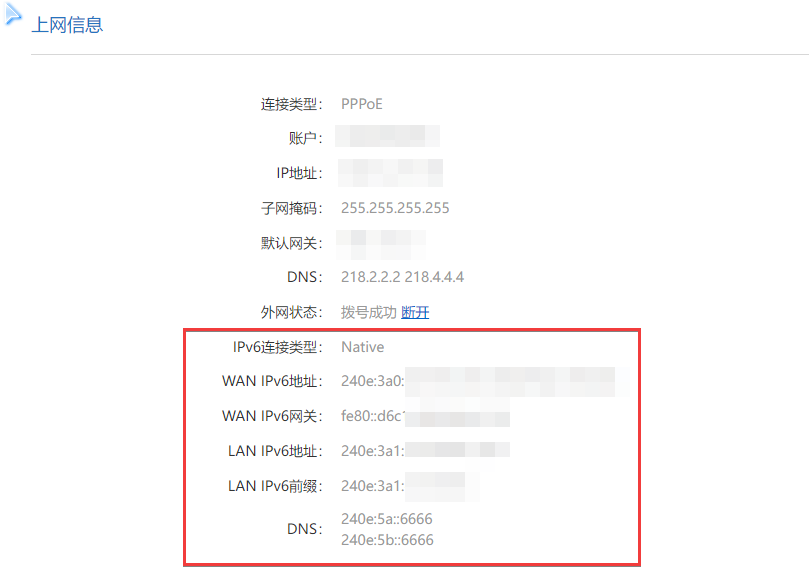
测试用例 

2.算法原理

1.状态表示

这里与路径问题不同的是每个位置都不止一个状态，因此开辟两个dp表，两个dp表中的dp[i]都表示在第i个位置的最大预约数，其中第i个位置可以被预约也可以不被预约 

2.状态转移方程

当第i个位置被预约：这就意味着第i-1个位置一定不会被预约，此时只需要求出第i-1个位置不被预约时的最大分钟数加上nums[i]就得出第i个位置的最大分钟数

当第i个位置不被预约：这代表第i-1个位置可以被预约也可以不被预约，因此需要计算出前一个位置的两种情况后去较大值即可

3.初始化

创建了两个dp表，一个代表指定位置被预约:f，一个代表指定位置不被预约:g，并且状态转移方程中需要用到i-1个位置，因此需要初始化两个dp表的第一个位置

f[0]:第一个位置被预约，直接就是nums[0]

g[0]:第一个位置不被预约，则直接为0

4.填表顺序

由于每个位置都需要前一个位置来计算，因此是从左到右填表的顺序

5.返回值

在走到两个dp表的末尾，由于不确定最后一个位置是否被预约，因此需要去f[n-1]与g[n-1]的较大值，并且注意考虑空表的情况，原来的表为空就返回0即可

3.实战代码

class Solution {
public:
    int massage(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n);
        vector<int> g(n);
        if(n == 0)
        {
            return 0;
        }
        f[0] = nums[0];
        for(int i = 1;i < n;i++)
        {
            f[i] = g[i-1] + nums[i];
            g[i] = max(f[i-1],g[i-1]);
        }
        int Max = max(f[n-1],g[n-1]);
        return Max;
    }
};