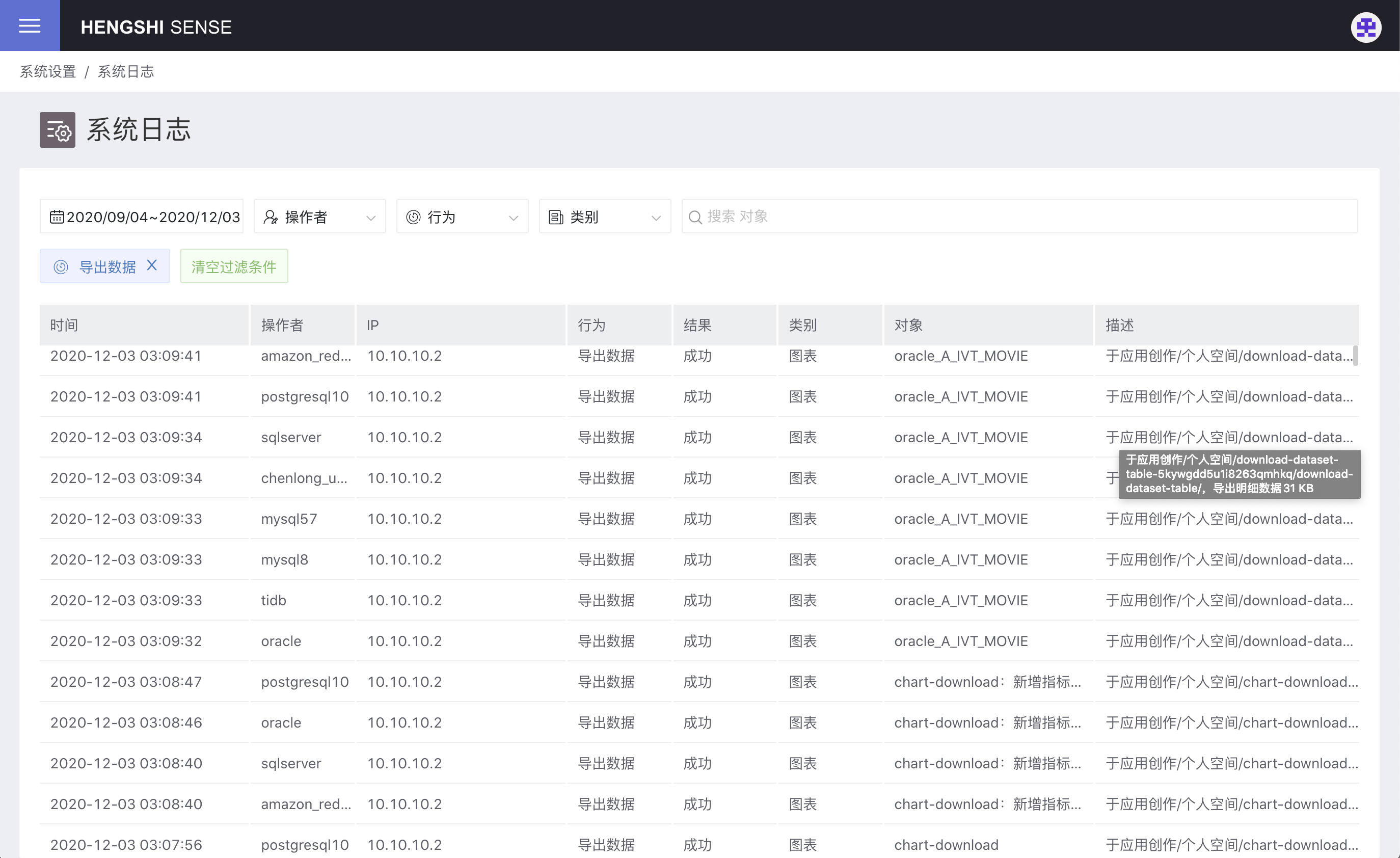
求法向量干什么？将点渲染成面

1、一个点垂直于一个曲线的切线叫法线

2、在点云中取一块区域，用最小二乘将区域中的点云拟合成一个面（贴合在曲面上的一个切面）在相近的区域计算出n个这样的面，用这个面求出法向量（每个法线对应着一个面），假如实际是一个相对平滑的表面，则向量的方向相近，可以直接cover成一个面；如果表面有很大的造型，则向量方向差异很大，则划分出相近的向量cover成不同面。

3、总结：用法线表达一个未知面的特征。

#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
// 包含相关头文件
#include <pcl/features/normal_3d.h>
#include <pcl/visualization/pcl_visualizer.h>

typedef pcl::PointXYZ PointT;
typedef pcl::PointNormal PointNT; // 也可以pcl::Normal,但无法用PCLVisualizer显示。

int main(int argc, char** argv)
{
	// 读取点云
	pcl::PointCloud<PointT>::Ptr cloud(new pcl::PointCloud<PointT>);
	pcl::io::loadPCDFile("../new.pcd", *cloud);
	
	// 计算法向量
	pcl::NormalEstimation<PointT, PointNT> nest;
	//nest.setRadiusSearch(0.01); // 设置拟合时邻域搜索半径，最好用模型分辨率的倍数
	nest.setKSearch(50); // 设置拟合时采用的点数
	nest.setInputCloud(cloud);
	pcl::PointCloud<PointNT>::Ptr normals(new pcl::PointCloud<PointNT>);
	nest.compute(*normals);

	for (size_t i = 0; i < cloud->points.size(); ++i)
	{	// 生成时只生成了法向量，没有将原始点云信息拷贝，为了显示需要复制原信息
		// 也可用其他方法进行连接，如：pcl::concatenateFields
		normals->points[i].x = cloud->points[i].x;
		normals->points[i].y = cloud->points[i].y;
		normals->points[i].z = cloud->points[i].z;
	}

	// 显示
	pcl::visualization::PCLVisualizer viewer;
	viewer.addPointCloud(cloud, "cloud");
	int level = 100; // 多少条法向量集合显示成一条
	float scale = 2.01; // 法向量长度
	viewer.addPointCloudNormals<PointNT>(normals, level, scale, "normals");

	viewer.spin();

	system("pause");
	return 0;
}