https://zhuanlan.zhihu.com/p/893338073

一、引言


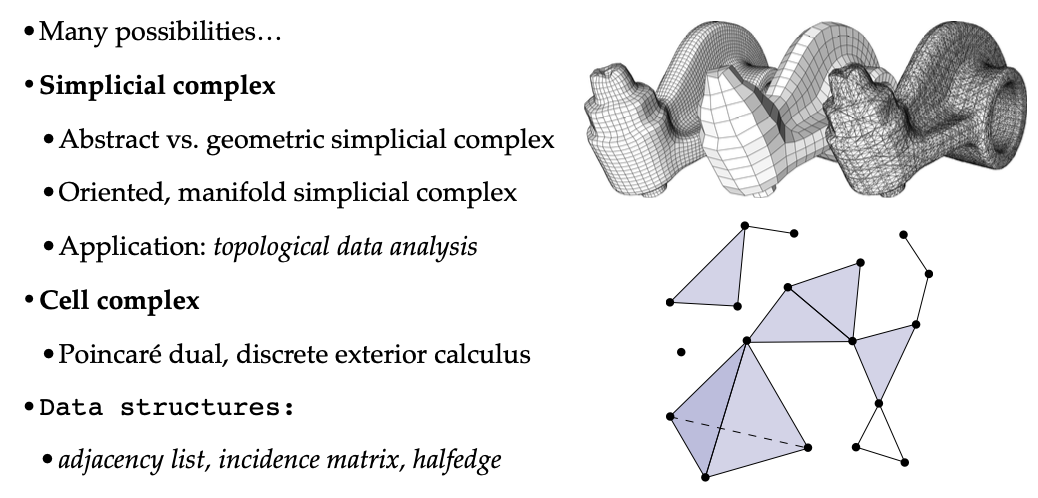在离散微分几何的广袤领域中，网格（Meshes）作为一个核心概念，犹如一座桥梁，连接着离散计算与连续几何的两个世界。它为我们理解和处理复杂的几何形状提供了一种离散化的表示方式，是构建众多几何算法和应用的基石。本文将深入探讨网格的多种形式和相关概念，包括简单复数（Simplicial Complex）的特性、细胞复合物（Cell Complex）及其庞加莱对偶（Poincaré Dual），以及用于表示网格的数据结构等内容。通过对这些知识的详细阐述，我们将揭示网格在不同领域的重要应用以及它与连续数学中的拓扑空间之间的紧密联系。

二、拓扑空间与凸集

（一）拓扑空间——抽象的连接概念


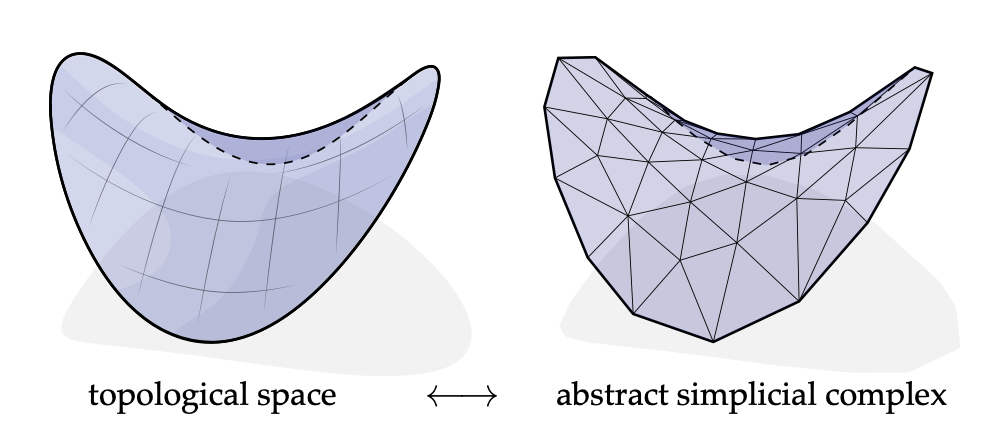拓扑空间是一个高度抽象的数学概念，它从一种宏观的视角描述了点与点之间的连接关系，而不涉及这些点在实际空间中的具体位置信息。这种抽象性使得拓扑空间能够涵盖各种不同类型的几何对象和结构，为我们研究几何形状的本质特征提供了一个统一的框架。从离散几何的角度来看，通过研究抽象的简单复数，我们能够逐渐建立起对拓扑空间的直观理解。因为抽象简单复数主要关注元素之间的连接方式，而忽略了它们在几何空间中的具体排列，这与拓扑空间的概念不谋而合。

（二）凸集——形状的凹凸特性

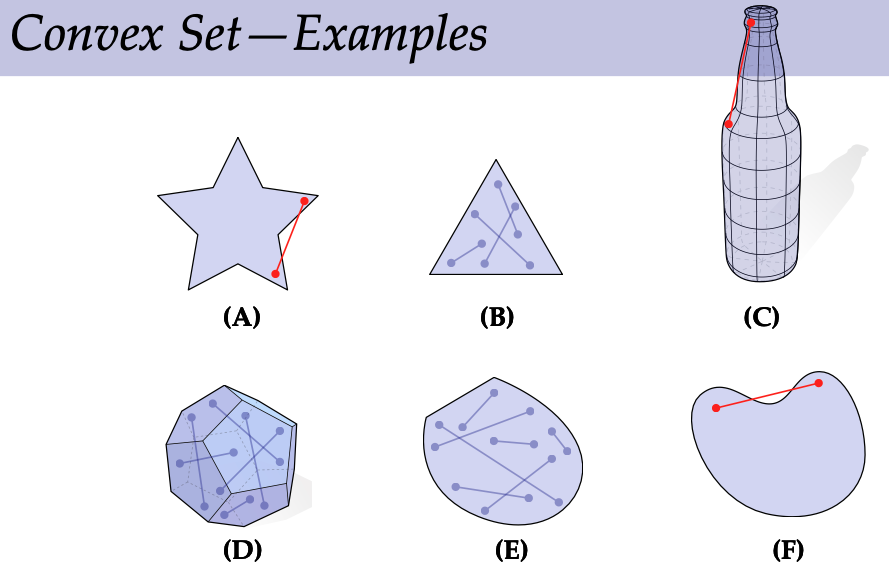
1. **定义** - 对于($ R^n $)空间中的一个子集(S)，我们通过一个严格的条件来定义凸集。如果对于(S)中的任意一对点(p)和(q)，连接这两点的线段完全包含在(S)中，那么我们就称(S)是凸集。这个定义从本质上刻画了凸集的特性，即集合内部的任意两点之间的连线不会超出该集合的范围。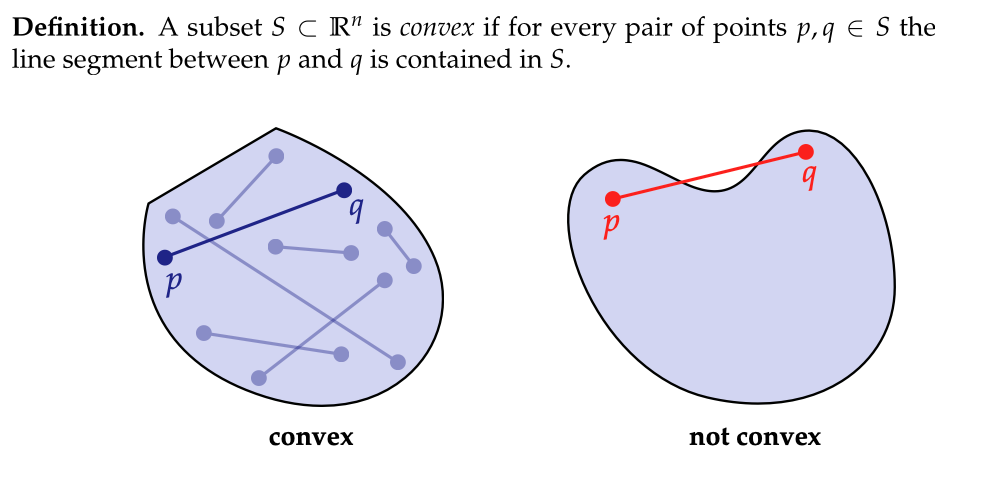

2. 示例
   • 为了更好地理解凸集的概念，我们来看一些常见的例子。三角形是凸集的一个典型代表，无论我们在三角形内部选取哪两个点，连接它们的线段必然都在三角形内部。而像星星、瓶子等形状则明显不是凸集。以星星为例，我们很容易找到两个角上的点，它们之间的连线会超出星星的形状范围。

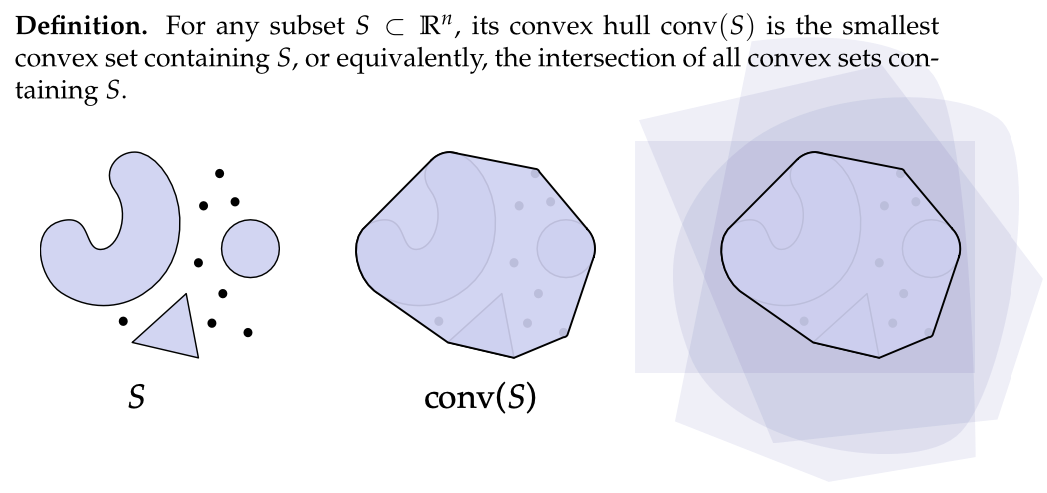
3. 凸包
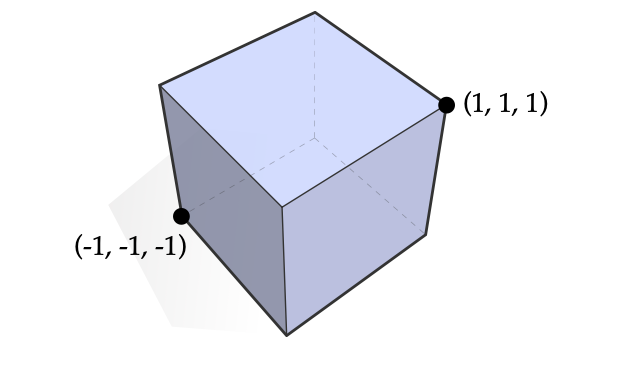
   • 对于$ (Rn) $的任意子集(S)，其凸包$ conv(S) $是一个重要的概念。它被定义为包含(S)的最小凸集，从另一个角度来说，它也等于所有包含(S)的凸集的交集。例如，考虑(R3)中所有坐标为$ (\pm1,\pm1,\pm1) $的点组成的集合，它的凸包就是一个立方体。我们可以这样来理解这个过程：这些点就像是立方体的顶点，由于任意两个顶点之间的连线都在立方体内，所以整个立方体就是这个点集的凸包。凸包的概念在很多几何问题中都有着重要的应用，它为我们提供了一种将非凸形状转化为凸形状的方式，从而简化一些几何分析。

三、单纯形（Simplex）——几何构建的基本单元

（一）基本概念——从向量独立到单纯形的形成


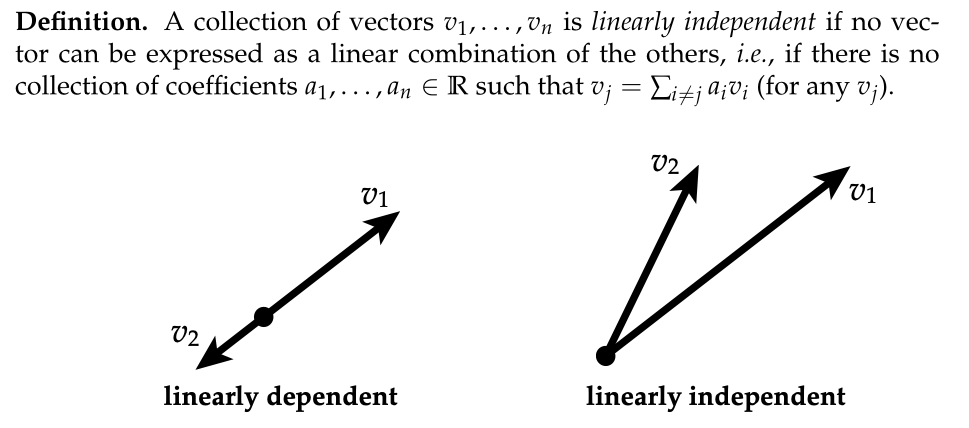1. 线性独立性与仿射独立性
   • 在探讨单纯形的定义之前，我们需要回顾线性代数中的两个重要概念：线性独立性和仿射独立性。向量($ v_1,\cdots,v_n $)是线性独立的，如果不存在一组实数系数($ a_1,\cdots,a_n $)（不全为零），使得其中一个向量可以表示为其他向量的线性组合。例如，两个不平行的向量就是线性独立的。在此基础上，我们引入仿射独立性的概念。对于一组点($ p_0,\cdots,p_k $)，当向量($ v_i = p_i - p_0 $)是线性独立的时候，我们就称这些点是仿射独立的。可以这样理解，仿射独立的点在空间中的位置关系是一种相对“独立”的状态，它们不会出现某个点可以通过其他点的简单线性组合来表示其位置的情况。

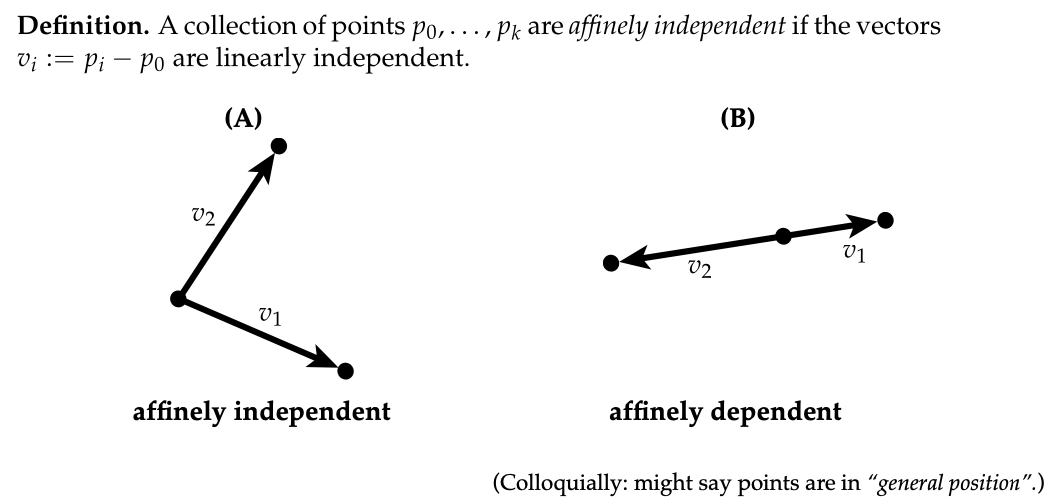
2. 定义
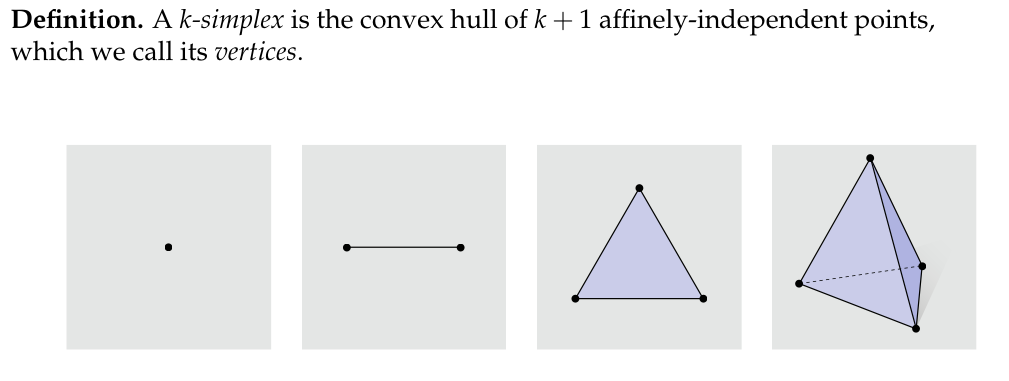
   • 有了仿射独立性的概念，我们就可以精确地定义(k)-单纯形。(k)-单纯形是(k + 1)个仿射独立点的凸包，这些点被称为单纯形的顶点。例如，当(k = 0)时，(k)-单纯形就是一个单独的点，这是一种最基本的情况；当(k = 1)时，它是一条线段，由两个仿邑独立的点构成其凸包；当(k = 2)时，它是一个三角形，由三个仿射独立的点确定；当(k = 3)时，它是一个四面体，由四个仿射独立的点组成。随着(k)的增大，单纯形的维度也在增加，但都是基于仿射独立点的凸包来定义的。

（二）重心坐标——单纯形内的坐标系统

1. **定义** - 在单纯形中，重心坐标是一个非常重要的概念。对于一个单纯形($ \sigma $)，内部的任何一个点(p)都可以表示为其顶点的非负加权组合，并且这些权重之和为(1)。这些权重就被称为重心坐标。例如，对于一个由两点(a)和(b)组成的(1)-单纯形，我们可以将内部的点(p)表示为($ p=(1 - t)a+tb $)，其中($ t\in[0,1] $)，这里的(t)和(1 - t)就是点(p)关于顶点(a)和(b)的重心坐标。

2. 标准**(n)****-单纯形**
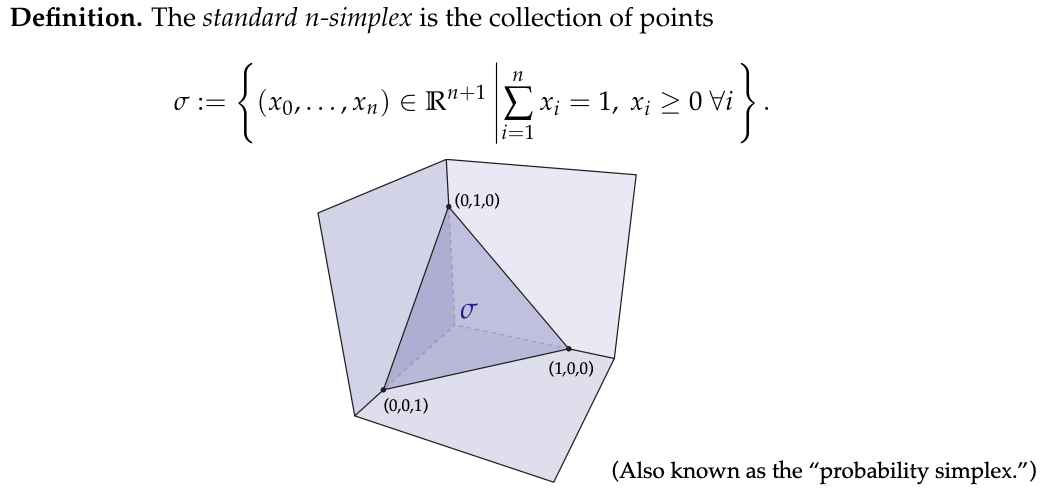
   • 还有一种特殊的单纯形叫做标准(n)-单纯形。它是($ R{n + 1} $))空间中坐标$ (x_0,\cdots,x_n) $满足($ \sum_{i = 1}{n}x_i = 1 $)且$ x_i\geq0\forall i $的点的集合。这个单纯形有一个很有趣的名字——概率单纯形。这是因为它的坐标性质与概率的性质相似，概率也是非负的且所有概率之和为(1)。标准(n)-单纯形在一些几何和概率相关的问题中有着特殊的应用。

四、单纯复数（Simplicial Complex）——单纯形的集合与规则

（一）几何单纯复数——具有几何规则的单纯形集合

1. **定义** - 几何单纯复数是单纯形的集合，但这个集合需要满足一定的规则。具体来说，其中任意两个单纯形的交集必须是这个集合中的一个单纯形，并且集合中每个单纯形的每个面也都要在集合中。这就好比一场有严格入场规则的聚会，只有符合条件的“成员”（单纯形）才能进入，而且每个“成员”的各个部分（面）也都要符合聚会的要求。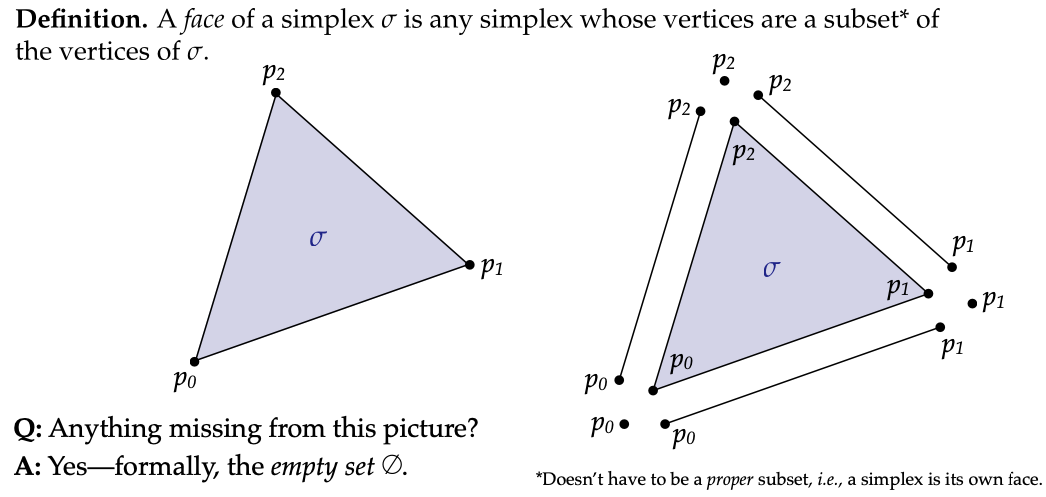

2. 示例
   • 我们来看一个具体的例子。假设有一个集合，它的顶点列举为($ 0,1,2,\cdots,10 $)。在这个集合中，我们可以找到一些单纯形，比如三角形({6,7,9})和({7,10,8})等，还有各种边和顶点。我们可以验证这些单纯形之间的关系是符合几何单纯复数的规则的。例如，三角形之间可能在边或顶点处相交，并且相交的部分也是符合要求的单纯形。

（二）抽象单纯复数——关注连接关系的单纯形集合

1. **定义** - 抽象单纯复数也是一个集合的集合，但它的规则与几何单纯复数有所不同。如果对于每个集合$ (\sigma\in S)，(\sigma) $的所有子集都包含在(S)中，那么(S)就是抽象单纯复数。这里面大小为(k + 1)的集合($ \sigma $)就是一个抽象单纯形。这种定义方式更侧重于单纯形之间的连接关系，而不关心它们在空间中的具体几何位置。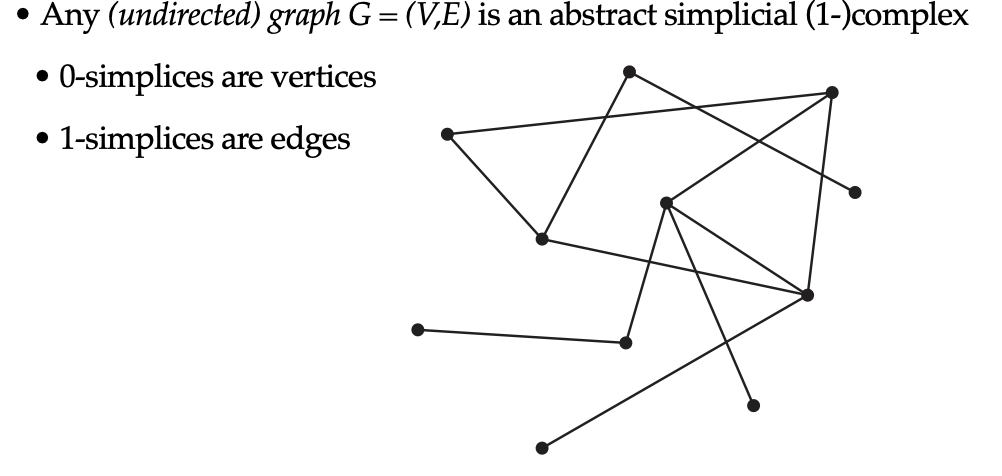

2. 示例
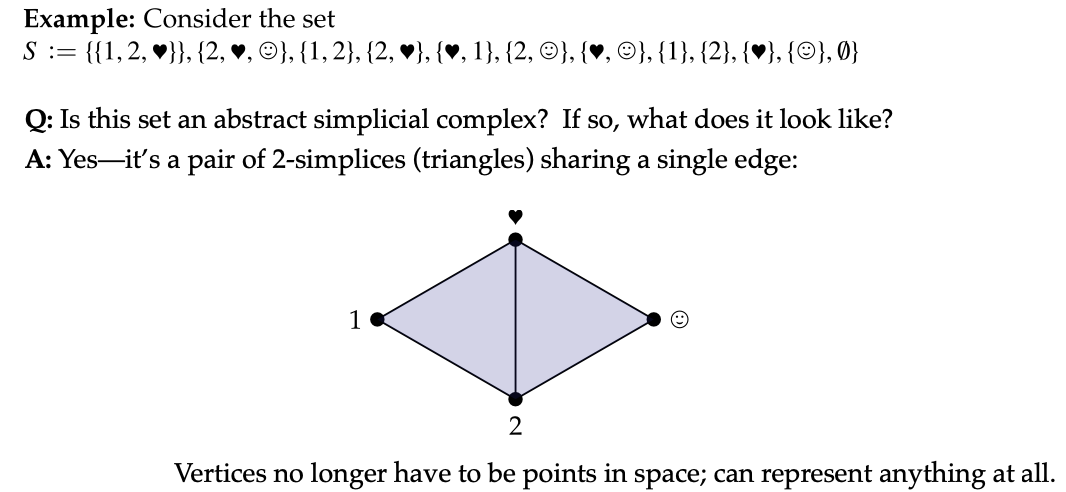
   • 例如无向图(G=(V,E))就是一个抽象单纯（(1)-复数。在这个图中，(0)-单纯形对应顶点，(1)-单纯形对应边。我们还可以考虑一些更复杂的集合例子。比如一个集合(S = {1,2,{2,3},{1,2},{2,4},{1},{2},{3},{4},{}})，我们可以验证它是否是一个抽象单纯复数。对于集合中的每个元素，我们检查它的所有子集是否也在集合中。例如，对于({2,3})，它的子集({2})和({3})以及空集都在集合(S)中，所以(S)是一个抽象单纯复数，它可以被看作是两个(2)-单纯形（三角形）共享一个边的结构，这里顶点不再局限于空间中的点，而是可以代表任何数据或对象。

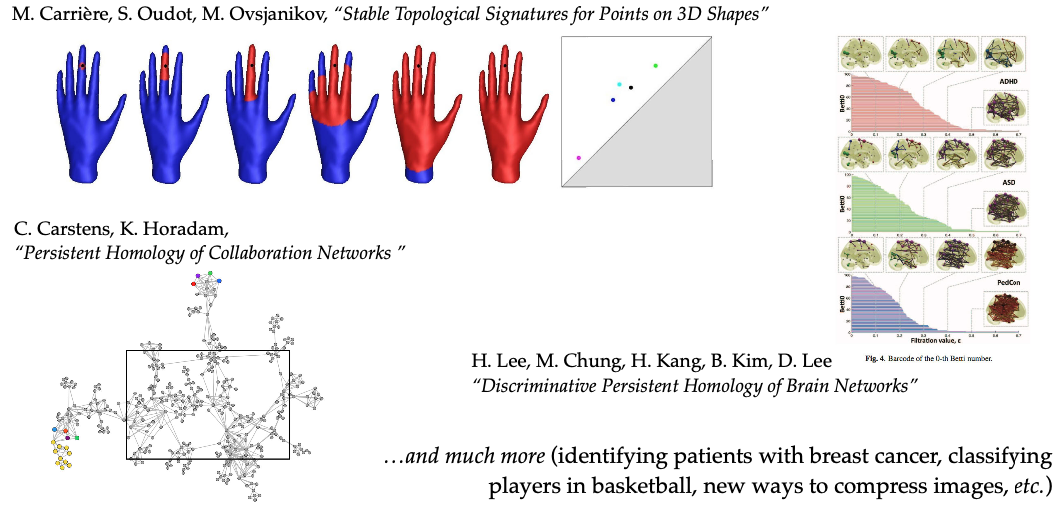
（三）应用：拓扑数据分析——从几何到连接的洞察

1. **持久同调：数据中的拓扑故事** - 在拓扑数据分析中，有一个重要的方法叫做持久同调。它的核心思想是在一定程度上忽略数据的几何结构，而是专注于数据的连接性来理解数据。 - 具体来说，我们首先在每个数据点周围“生长”球。当这些球发生重叠时，我们根据重叠的情况将它们连接成不同维度的单纯形。例如，如果两个球重叠，我们就用(1)-单纯形（边）连接它们；如果三个球重叠，我们就用(2)-单纯形（三角形）连接它们，以此类推。 - 然后我们跟踪一些特征的“出生”和“死亡”。这些特征包括连接组件、洞等。我们把这些信息绘制在一个持久化图上。在这个图中，每个点都代表一个特征，它的(x)坐标表示该特征首次出现的时间（“出生”时间），(y)坐标表示该特征消失的时间（“死亡”时间）。 - 通过观察这个持久化图，我们可以发现一些有趣的现象。持久时间长的特征可能是数据中“真实”的、有意义的结构，而快速出现然后消失的特征可能是噪声或者是不太重要的局部结构。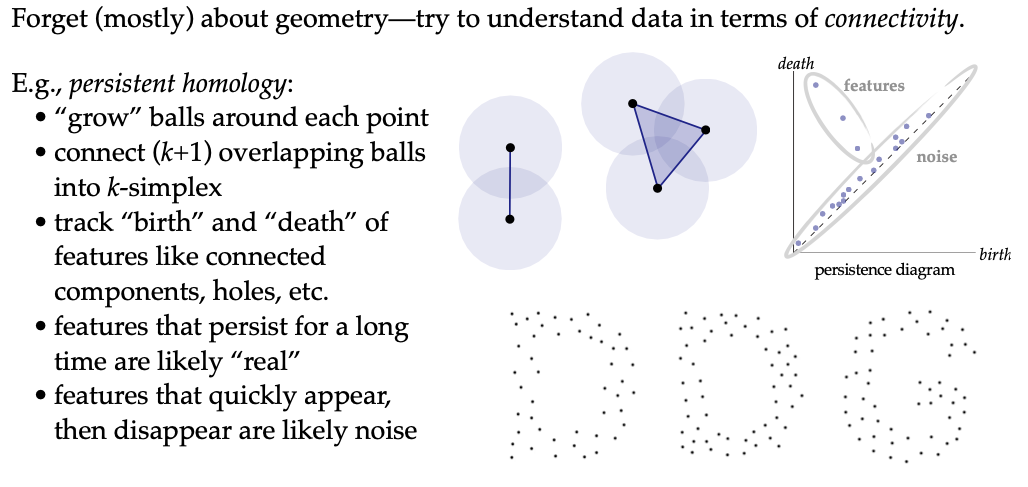

2. 应用领域的广泛探索
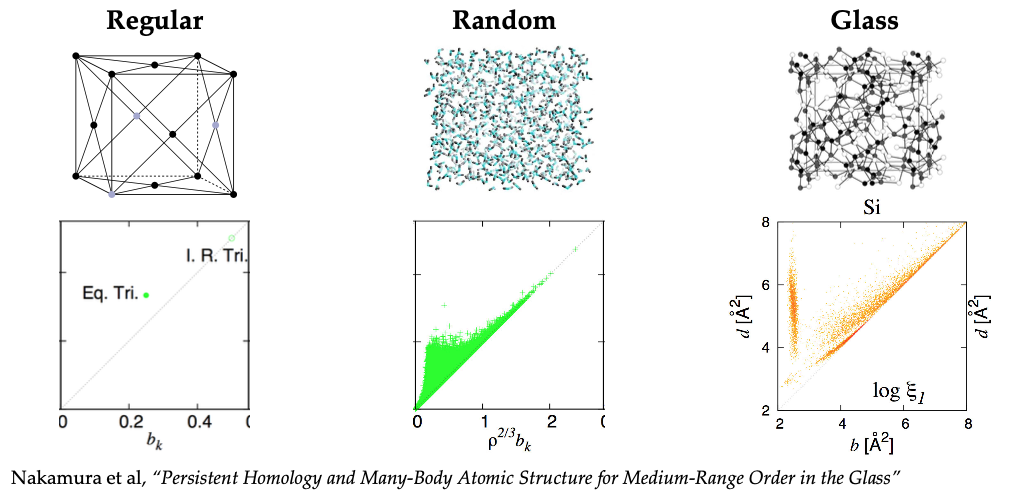
   • 这种方法在很多领域都有重要的应用。例如在材料科学中，我们可以通过分析材料中原子的位置关系（将原子看作数据点）来了解材料的性质。如果我们对材料中的一堆原子位置应用持久同调方法，可能会发现一些与材料结构相关的特征。

- 在大脑网络分析中，我们可以将神经元之间的连接看作是数据的连接关系，通过持久同调方法来了解大脑的网络结构和功能。比如，我们可以区分健康的大脑和患有某种疾病的大脑，因为它们的神经元连接网络可能具有不同的拓扑特征。
- 此外，在社交网络分析、图像压缩等领域，持久同调方法也有着潜在的应用价值，它为我们从拓扑的角度理解数据提供了一种新的工具。

五、单纯复数的解剖结构——深入内部的结构剖析

（一）相关概念——单纯复数的各个部分

1. **闭包：最小的包含外壳** - 闭包是一个关于单纯形集合的重要概念。它是包含给定单纯形集合的最小单纯复数。也就是说，我们给定一个单纯形的集合，闭包就是能够包含这些单纯形并且自身也是单纯复数的最小集合。例如，如果我们给定一个三角形和一条边组成的集合，它的闭包不仅要包含这个三角形和边，还要包含三角形的所有边、顶点以及边的所有顶点等。 2. **星：围绕的单纯形中心** - 星是包含给定单纯形子集的单纯形的并集。可以想象成以某个单纯形子集为中心，周围所有包含这个子集的单纯形所组成的集合。例如，如果我们以一个顶点为中心，那么它的星就是所有包含这个顶点的三角形和边等单纯形的集合。 3. **链接：边界的特殊区域** - 链接是闭包的星减去星的闭包。它定义了一个特殊的区域，这个区域可以帮助我们更好地理解单纯复数的边界和内部结构的关系。例如，对于一个顶点，它的链接可能是一个围绕顶点的边环（在某些情况下）。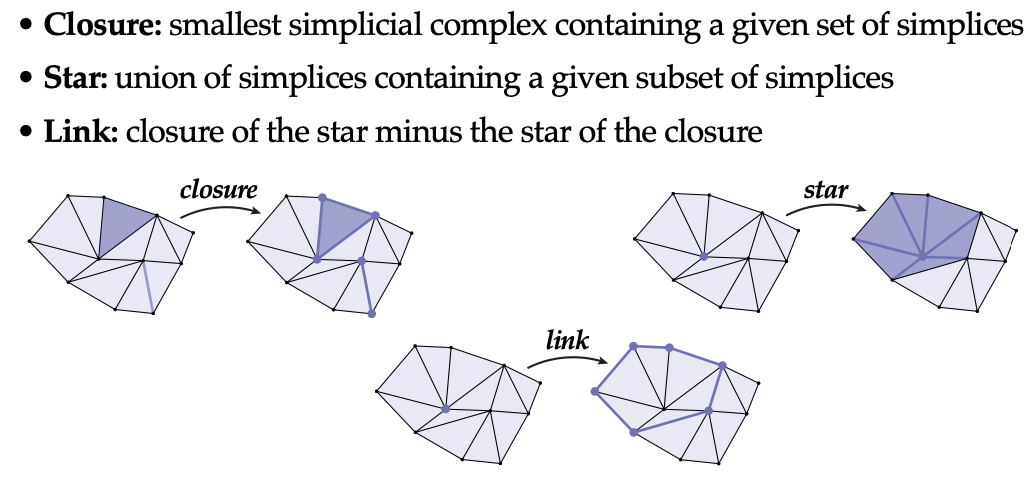

（二）符号表示——给单纯复数的元素贴标签

1. 对于单纯(1)-复数（图），我们经常用(G=(V,E))来表示，其中(V)是顶点，(E)是边。 2. 对于单纯(2)-复数（在前文中提到的三角形网格），我们常用(K=(V,E,F))来表示，其中(V)是顶点，(E)是边，(F)是面。这里需要注意的是，面是指顶级的面，不同于单纯形的一般面概念。这些符号表示为我们在研究和讨论单纯复数时提供了一种简洁明了的方式，方便我们区分不同类型的单纯复数和它们的组成元素。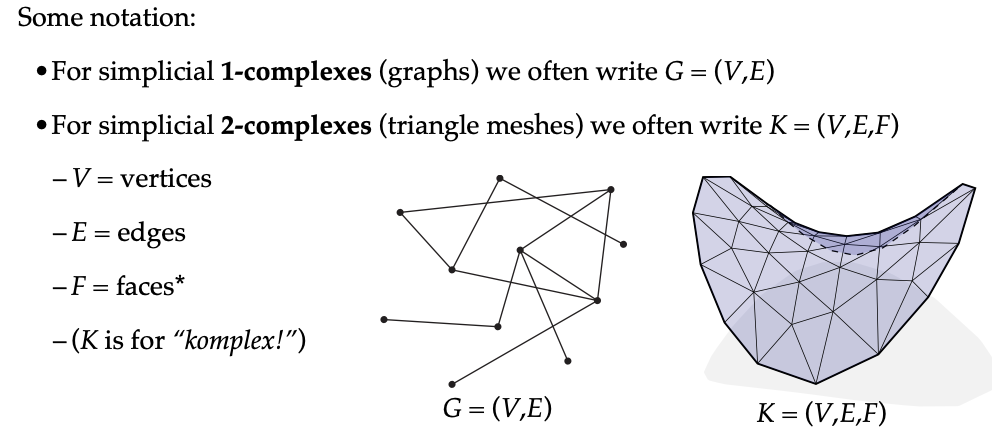

六、定向单纯复数（Oriented Simplicial Complex）——赋予方向的单纯形集合

（一）方向的定义——单纯形的方向之旅

1. **(****1****)****-单纯形方向：简单的起点** - 我们先来探讨(1)-单纯形的方向。对于(1)-单纯形({a,b})，我们可以用有序元组((a,b))或((b,a))来表示它的方向。这就好比在一条线段上确定了一个方向，是从(a)到(b)还是从(b)到(a)。这个方向的定义在后续的积分计算等方面会非常有用。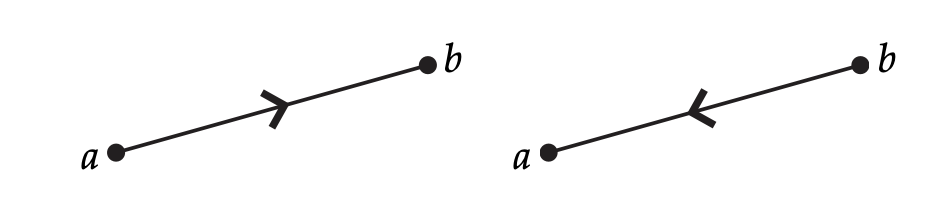

2. (2)****-单纯形方向：三角形的旋转方向
   • 对于(2)-单纯形，它的方向是由顶点的缠绕顺序给出的。比如说对于一个三角形，如果我们把顶点标记为(a,b,c)，那么它的方向可以用((a,b,c))等三元组表示。不同的循环移位描述的是相同的定向(2)-单纯形。例如，((a,b,c))、((b,c,a))和((c,a,b))都表示同一个定向的三角形，它们的方向是按照顺时针（或逆时针）的顺序围绕三角形的顶点。

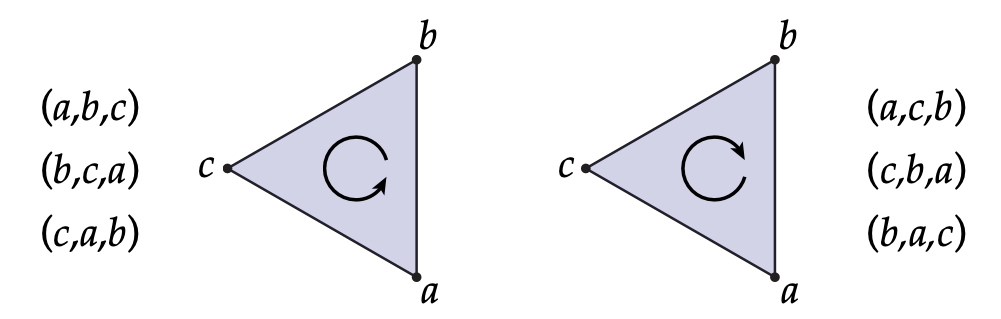
3. (k)****-单纯形方向：通用的方向规则
   • 对于(k)-单纯形，它是一个有序元组，直到偶数排列。这意味着它有两种可能的方向，对应偶数或奇数排列的顶点。例如，对于(0)-单纯形（单个顶点），它只有一个方向（正向），因为它只有一种排列方式。对于一个四面体（(3)-单纯形），我们可以列举出它的两种可能的方向对应的顶点排列，如((1,2,3,4))（正向）和(1,2,4,3)（负向）等。

（二）定向单纯复数的定义：有方向的单纯形聚会

+ 定向单纯复数就是一个单纯复数，其中每个单纯形都被赋予一个方向，也就是顶点的排序直到偶数排列。我们可以通过其代表性的面向元组之一来指定一个有向的单纯形。这就好比给参加聚会的每个人都指明了一个方向，使得整个聚会有了一种有序的结构。

（三）相对方向：不同单纯形之间的方向关系

1. **定义：方向的比较规则** - 两个不同的定向单纯形如果在它们交集处的两个最大面具有相反的方向，则它们具有相同的相对方向。这里的最大面是指在交集处维度最高的单纯形。 2. **示例：三角形的相对方向判断** - 我们以两个沿边相交的三角形为例来具体说明。假设一个三角形的顶点顺序为((a,b,c))，边(bc)的方向是从(b)到(c)；另一个三角形的顶点顺序为((c,d,b))，边(bc)的方向是从(c)到(b)。因为在它们交集处的边(bc)在两个三角形中的方向相反，所以这两个三角形具有相同的相对方向。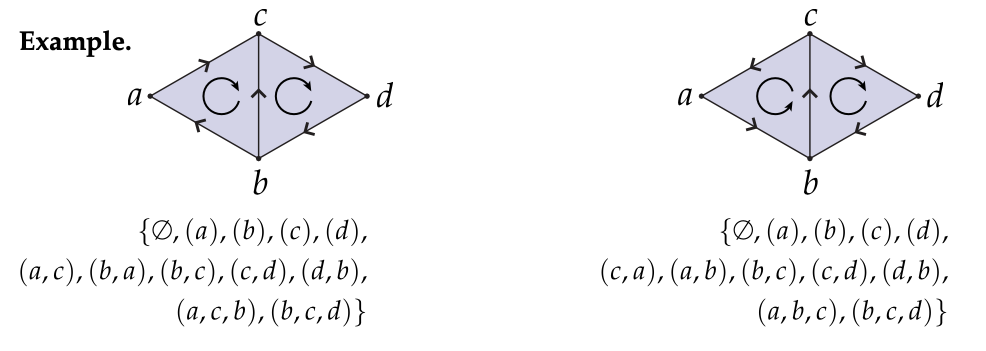

七、细胞复合物（Cell Complex）与庞加莱对偶（Poincaré Dual）——更广阔的几何视野

（一）细胞复合物——复杂形状的新视角


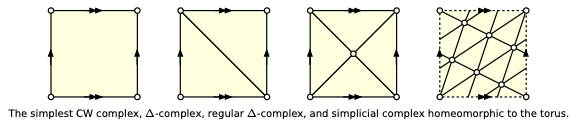1. 概念介绍：细胞的组合世界
   • 细胞复合物是比单纯复数更一般的网格结构。它由不同维度的细胞组成，这些细胞可以是点、线段、多边形、多面体等，并且满足一定的组合规则。这就像一个由各种形状的积木组成的大模型，每个积木都有它自己的特点和规则。例如，一个细胞复合物可能包含顶点（0 - 细胞）、边（1 - 细胞）、面（2 - 细胞）以及三维的体（3 - 细胞）等。
2. 与单纯复数的关系：特殊与一般的对比

• 单纯复数可以看作是细胞复合物的一种特殊情况，其中细胞的结构更加规则，都是单纯形的形式。细胞复合物在一些应用中提供了更灵活的描述方式，例如在描述某些具有复杂拓扑结构的物体时，它可以更好地适应不同维度和形状的组合。这就像单纯复数是一种标准的积木，而细胞复合物是一种可以自由组合各种形状积木的套装。

（二）庞加莱对偶——几何中的对称之美

1. **基本思想：对偶的奥秘** - 庞加莱对偶是一种在拓扑学和几何中非常重要的对偶概念。对于一个给定的拓扑空间或网格结构（如单纯复数或细胞复合物），庞加莱对偶将其与另一个具有相关拓扑和几何性质的结构相关联。这种对偶关系在很多方面都有体现，例如在计算拓扑不变量、理解空间的同调性质以及在离散外部微积分中都起着关键作用。这就像一面镜子，把一个几何结构映射到另一个相关的结构上，让我们可以从不同的角度理解几何。 2. **示例说明：二维的对偶之美** - 我们以一个简单的二维单纯复数（三角形网格）为例，它的庞加莱对偶是一个由顶点和边组成的图结构，其中原单纯复数中的面（三角形）对应对偶结构中的顶点，原单纯复数中的边对应对偶结构中的边，并且边的连接关系是根据原单纯复数中面与面之间的邻业关系确定的。这种对偶关系可以帮助我们从不同的角度理解网格的拓扑结构，并且在一些计算中可以简化问题的处理。这就像我们通过镜子看到了一个物体的另一个角度，让我们对这个物体有了更全面的了解。

八、数据结构——存储几何的智慧

（一）邻接列表（Adjacency List）——简洁的连接记录

1. **结构描述：记录邻接关系的清单** - 邻接列表是一种用于表示网格中元素之间邻接关系的数据结构。对于一个图（可以看作是一种特殊的单纯复数），邻接列表通常为每个顶点存储一个清单，这个清单包含了与该顶点相邻的其他顶点。在更复杂的网格结构中，如三角形网格，邻接列表可以扩展到存储面与面之间、边与边之间以及顶点与面、边之间的邻接关系。这就像我们为每个小伙伴记录他周围的小伙伴名单一样，很简洁明了。 2. **优点：节省空间与高效遍历** - 它具有节省存储空间的优点，尤其是在稀疏图或网格中，即当顶点之间的邻接关系相对较少时，邻接列表只需要存储实际存在的邻接关系，而不需要为每个顶点分配固定大小的邻接数组。此外，它在遍历图或网格以查找相邻元素时也具有较高的效率。这就像我们只记录实际存在的小伙伴关系，不会浪费空间，而且找小伙伴的时候也很方便。

（二）入射矩阵（Incidence Matrix）——统一的关系描述

1. **结构描述：矩阵中的关系网** - 入射矩阵是一个矩阵，用于表示网格中不同维度元素之间的入射关系。例如，在一个三角形网格中，如果我们有顶点、边和面三种元素，入射矩阵的行可以对应顶点，列可以对应边和面。矩阵中的元素表示相应的顶点与边或面之间是否存在入射关系（通常用0或1表示）。这就像我们用一个大表格来记录不同小伙伴之间的各种关系，很清晰。 2. **优点：统一描述与方便运算** - 它提供了一种统一的方式来描述网格中所有元素之间的关系，并且在一些算法中，如计算拓扑不变量或进行网格变换时，可以方便地利用矩阵运算来处理这些关系。同时，它对于理解网格的结构和拓扑性质也有一定的帮助，通过观察入射矩阵的模式可以获取关于网格的元素连接方式的信息。

（三）半边网格（Halfedge）——高效的拓扑处理结构

1. **结构描述：半边的巧妙运用** - 半边网格是一种在计算机图形学和几何处理中常用的数据结构。它基于半边的概念，即对于每条边，将其分成两个半边，每个半边都有自己的方向和相关的顶点、面等信息。通过这种方式，可以更方便地处理网格中的拓扑关系，例如在处理面与面之间的邻接关系、边的像穿以及网格的修改操作时，半边网格都提供了一种高效的方法。 2. **优点：灵活高效的拓扑操作** - 它在处理网格的拓扑操作时具有很高的灵活性和效率。例如，在进行网格细分、合并等操作时，半边网格可以很容易地跟踪和更新网格的拓扑结构。同时，它也可以更好地适应不同形状和复杂度的网格，相比于其他数据结构，它在处理具有复杂拓扑结构的网格时表现出更好的性能。

九、总结

离散微分几何中的网格概念涵盖了单纯复数、细胞复合物等多种形式，并且涉及到方向、拓扑数据分析、解剖结构以及相关的数据结构等多个方面。这些知识对于理解和处理几何形状的离散表示以及在计算机图形学、材料科学、拓扑数据分析等多个领域的应用都具有重要的意义。

通过深入研究网格的各种性质和相关概念，我们可以更好地对几何对象进行建模、分析和处理，从而为解决实际问题提供有效的工具和方法。例如，在计算机图形学中，网格可以用于精确地表示三维模型的形状和结构，通过对网格的优化处理，如简化、细分、平滑等操作，可以提高模型的渲染效率和视觉质量。在材料科学中，网格可以模拟材料的微观结构，通过分析网格的拓扑特征和几何性质，可以了解材料的物理性能和力学行为。在拓扑数据分析中，网格为我们提供了一种有效的数据结构来表示和分析复杂的数据集合，通过计算网格的拓扑不变量和同调群，可以发现数据中的隐藏结构和模式。

总之，网格是离散微分几何中一个非常重要的概念，它为我们在不同领域的研究和应用提供了坚实的基础，并且随着计算机技术的不断发展和应用需求的不断增加，网格的研究和应用也将不断深入和拓展。