代码随想录算法训练营第二十六天|669. 修剪二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树

669. 修剪二叉搜索树

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

669.修剪二叉搜索树

669.修剪二叉搜索树1

思路：

首先判断根节点是否在区间内，如果正常在区间内则递归判断孩子节点；否则如果不在区间内，小于区间则说明左子树必然也不在区间内，直接令右孩子作为根节点，反之亦然。而在递归过程中，如果遇到根节点在区间内，孩子节点不在区间内，和以上相同的道理，左孩子节点如果不在区间，左孩子的左孩子必然不在区间内，所以只需要考虑【左孩子】的【右孩子】，反之，如果右孩子不在区间内，只需要考虑【右孩子】的【左孩子】。

代码实现如下：（备注的逻辑也能AC，原本一直debug的原因是递归调用的节点错误，自己的逻辑虽然能A但感觉不是很好的思路，实现过程较长）

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:

        if not root:

            return None

       

        #if root.val not in range(low, high+1):

        #    if root.val < low and root.right:

        #        return self.trimBST(root.right, low, high)

        #    elif root.val > high and root.left:

        #        return self.trimBST(root.left, low, high)

        #    else:

        #        return None

        if root.val < low:

            root = root.right

            return self.trimBST(root, low, high)

        elif root.val > high:

            root = root.left

            return self.trimBST(root, low, high)

       

        while root.left and root.left.val not in range(low, high+1):

            root.left = root.left.right

        self.trimBST(root.left, low, high)



        while root.right and root.right.val not in range(low, high+1):

            root.right = root.right.left

        self.trimBST(root.right, low, high)



        return root

修正精简：

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:

        if not root:

            return None

       

        if root.val < low:

            return self.trimBST(root.right, low, high)

        elif root.val > high:

            return self.trimBST(root.left, low, high)

       

        root.left = self.trimBST(root.left, low, high)

        root.right = self.trimBST(root.right, low, high)



        return root

规范代码：（思路清晰，记录学习）

class Solution {

public:

    TreeNode* trimBST(TreeNode* root, int low, int high) {

        if (root == nullptr ) return nullptr;

        if (root->val < low) {

            TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点

            return right;

        }

        if (root->val > high) {

            TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点

            return left;

        }

        root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子

        root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子

        return root;

    }

};

迭代法：（第一次自己实现递归的时候，思路更像迭代，这个方法的思路过程应该自己找时间重新思考，是否将递归和迭代没有区分开来）

class Solution:

    def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:

        if not root:

            return None

        

        # 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭

        while root and (root.val < L or root.val > R):

            if root.val < L:

                root = root.right  # 小于L往右走

            else:

                root = root.left  # 大于R往左走

        

        cur = root

        

        # 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况

        while cur:

            while cur.left and cur.left.val < L:

                cur.left = cur.left.right

            cur = cur.left

        

        cur = root

        

        # 此时root已经在[L, R] 范围内，处理右孩子大于R的情况

        while cur:

            while cur.right and cur.right.val > R:

                cur.right = cur.right.left

            cur = cur.right

        

        return root

108.将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

示例:

108.将有序数组转换为二叉搜索树

思路：说实话这道简单题一开始竟然没思路。。看了文字解析觉得自己真是难题做多简单题思路突然就卡死了，可能自己还是太死脑筋。

本题思路很明确，由于是严格有序递增数组，所以构建二叉树的时候，根节点一定是有序数组中最中间的那个节点，这样根节点就将两个数组分为了两个子数组，刚好对应了它的左右子树，根据这个过程，我们不难写出递归函数。（同样需要注意的是，在递归的时候应该遵照循环不变量原则，在这里我选择严格左闭右闭）

递归三部曲：

参数和返回值：被分割的有序数组arr、起点下标left和结尾下标right作为传入参数，得到的中间节点作为返回值。
终止条件：当left>right，即无法构成一个子数组时，返回None
递归逻辑：传入的数组是应该被构建的树，所以计算数组的最中间元素来构建节点作为本树的根节点，而该节点的左子树是对左子数组进行递归得到的孩子节点，同理右子树是右子数组进行递归得到的孩子节点。

代码实现如下:

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:

        root = self.traversal(nums, 0, len(nums)-1)

        return root



    def traversal(self, arr: List[int], left:int, right:int) -> Optional[TreeNode]:

        if left > right:

            return None

       

        mid = left + ((right - left)//2)

        root = TreeNode(arr[mid])

        root.left = self.traversal(arr, left, mid-1)

        root.right = self.traversal(arr, mid+1, right)

        return root

规范代码：（递归以上复现一致）

递归精简(自身调用)：

class Solution:

    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:

        if not nums:

            return

        mid = len(nums) // 2

        root = TreeNode(nums[mid])

        root.left = self.sortedArrayToBST(nums[:mid])

        root.right = self.sortedArrayToBST(nums[mid + 1 :])

        return root

迭代：

from collections import deque

class Solution:

    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:

        if len(nums) == 0:

            return None

        

        root = TreeNode(0)  # 初始根节点

        nodeQue = deque()   # 放遍历的节点

        leftQue = deque()   # 保存左区间下标

        rightQue = deque()  # 保存右区间下标

        

        nodeQue.append(root)               # 根节点入队列

        leftQue.append(0)                  # 0为左区间下标初始位置

        rightQue.append(len(nums) - 1)     # len(nums) - 1为右区间下标初始位置



        while nodeQue:

            curNode = nodeQue.popleft()

            left = leftQue.popleft()

            right = rightQue.popleft()

            mid = left + (right - left) // 2



            curNode.val = nums[mid]  # 将mid对应的元素给中间节点



            if left <= mid - 1:  # 处理左区间

                curNode.left = TreeNode(0)

                nodeQue.append(curNode.left)

                leftQue.append(left)

                rightQue.append(mid - 1)



            if right >= mid + 1:  # 处理右区间

                curNode.right = TreeNode(0)

                nodeQue.append(curNode.right)

                leftQue.append(mid + 1)

                rightQue.append(right)



        return root

538.把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。

示例 1：

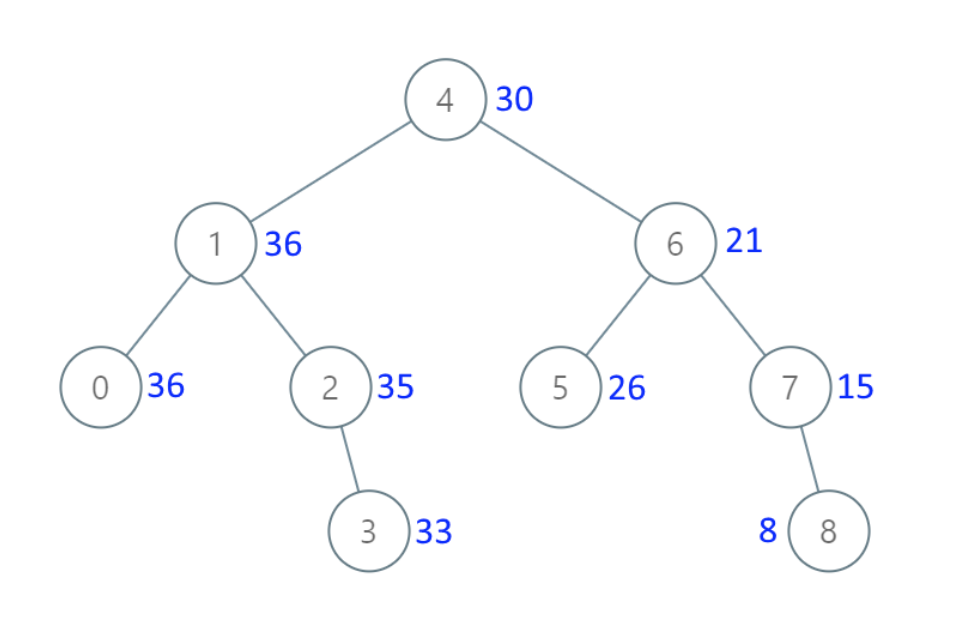
538.把二叉搜索树转换为累加树

输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值互不相同。
给定的树为二叉搜索树。

思路：

可以发现，如果将该二叉搜索树转化为有序的递减序列，累加树的每个节点值在递减序列中可以表现为：本节点的【累加值】=前一个节点【累加值】+本节点【val值】。这也是从累加树的定义中可以得到的，对于最大的节点，大于等于他的节点只有他自己。而对下一个大节点而言，大于等于他的节点是他自己加上前面一个符合条件的节点，所以累加值的计算逻辑就出来了。而我们又知道，二叉搜索的中序遍历可以得到从小到大的有序数列，所以想要得到从大到小的有序遍历的话，那就是【中序遍历】的【倒序】，即右-中-左。

递归三部曲：

参数和返回值：参数是传入节点，返回值是None。
终止条件：节点为空时，返回
递归逻辑：按照右-中-左顺序递归遍历，处理本节点时，记录全局cur变量，先将本节点原val值加到cur中，得到记录当前累加到的值，作为为本节点累加值的赋值。

代码实现如下：

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:

        self.cur = 0

        self.visit(root)

        return root



    def visit(self, node: Optional[TreeNode]) -> None:

        if not node:

            return



        self.visit(node.right)

        self.cur += node.val

        node.val = self.cur

        self.visit(node.left)

补充一个递归：（用pre，和自己实现的区别在于，我用的cur先加，然后直接赋值。Pre的话是记录上一个点的累加值，然后再与本节点val相加）

# Definition for a binary tree node.

# class TreeNode:

#     def __init__(self, val=0, left=None, right=None):

#         self.val = val

#         self.left = left

#         self.right = right

class Solution:

    def convertBST(self, root: TreeNode) -> TreeNode:

        self.pre = 0  # 记录前一个节点的数值

        self.traversal(root)

        return root

    def traversal(self, cur):

        if cur is None:

            return        

        self.traversal(cur.right)

        cur.val += self.pre

        self.pre = cur.val

        self.traversal(cur.left)

迭代：

class Solution:

    def __init__(self):

        self.pre = 0  # 记录前一个节点的数值

    

    def traversal(self, root):

        stack = []

        cur = root

        while cur or stack:

            if cur:

                stack.append(cur)

                cur = cur.right  # 右

            else:

                cur = stack.pop()  # 中

                cur.val += self.pre

                self.pre = cur.val

                cur = cur.left  # 左

    

    def convertBST(self, root):

        self.pre = 0

        self.traversal(root)

        return root