概述

论文地址：https://arxiv.org/pdf/2403.14404
源码地址：https://github.com/jhbastek/physicsinformeddiffusionmodels
扩散模型在逼近非常复杂的数据分布方面具有极高的性能和多功能性，近年来在自然科学领域的应用迅速扩展。鉴于其在科学背景下的应用，经常会出现这样的情况：对于某一类问题，数据所遵循的控制方程是明确已知的，因此希望给出一个正则化，使数据遵循这些控制方程。迄今为止，许多扩散模型的科学应用都是纯粹由数据驱动的，所生成的样本是否遵循物理规律并不重要。在这项研究中，我们研究了为扩散模型提供物理正则化的理论方法，从而使生成的样本服从支配方程，并通过数值实验证明了这些方法的实用性。

研究背景

扩散模型是当前人工智能的一个重要基础。扩散模型非常善于逼近数据所遵循的复杂分布，其应用已迅速普及。近年来，扩散模型在自然科学领域也得到了应用。然而，许多扩散模型的科学应用纯粹是为了从数据中逼近数据所遵循的分布，对其与科学知识的结合考虑不足。在特定情况下，如果数据所遵循的控制方程作为科学发现已被明确知晓，那么就需要建立对扩散模型进行物理约束的方法，从而使生成的样本遵循控制方程。在此背景下，本研究从理论上探讨了对扩散模型施加物理正则化的问题。

建议方法

在本研究中，有几项重要内容将在此介绍。

扩散模型

扩散模型是一种最先进的生成模型。简而言之，扩散模型的目的是对数据 x0 所遵循的分布 q(x0) 进行近似和建模。为此，扩散模型会考虑一系列从 x0 到 xT 的 T 步数据，并在每一步添加高斯噪声，从而使 xT 为纯高斯噪声。这个过程称为前向扩散过程，定义如下。

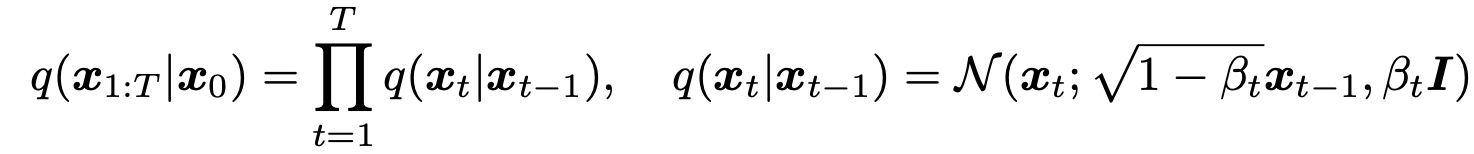
其中 {β∈(0,1)}Tt=1 是决定扩散过程的参数。由高斯过程生成的一系列样本作为逆运算也定义如下。

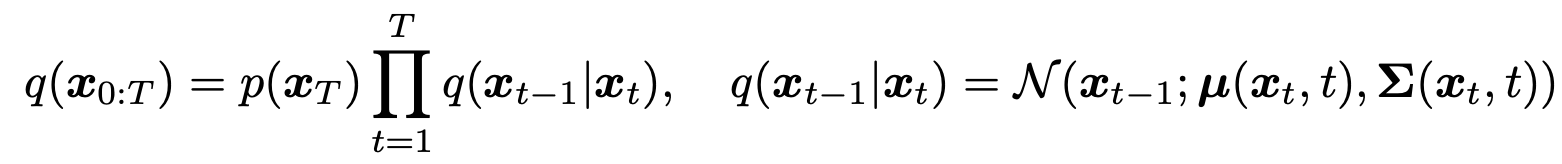
其中，未知分布 q(xt−1|xt)被神经网络近似为pθ$(x\_t-1|x\_t)$。最后，按照 Ho 等人的简化方法，用以下损失函数进行训练。

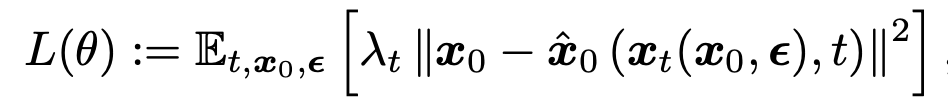
换句话说，从概念上讲，对它进行训练是为了使添加噪音然后去除噪音的结果 ^x0 与原始数据 x0 之间的误差很小。以上是对扩散模型的简要介绍。

执政方程

一般来说，治理方程可以抽象地表达如下。

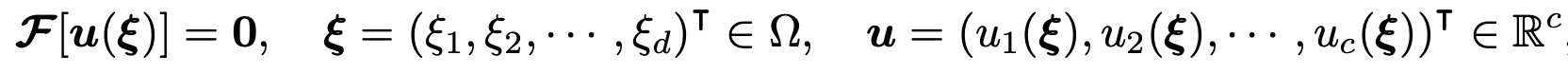
此外，还考虑了以下一般边界条件

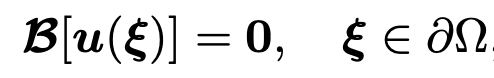
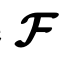
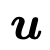然而，这里是抽象微分算子，是边界条件，是控制方程的解。在本研究中，假定由扩散模型生成的样本 x0 满足包括上述边界条件在内的控制方程。在本研究中，x0 被视为图像形式的数据，例如代表力学问题中应力分布的图像。根据该控制方程，定义了以下残差。

因此，简单地说，这个残差可以衡量是否满足治理方程。

物理信息扩散模型

目标函数的设计

在本研究中，为避免影响扩散模型的随机视角，引入了一个假定的残差 ^r 并假定其服从以下分布

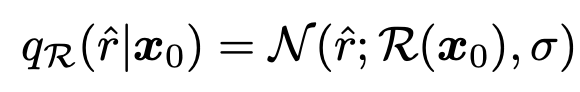
据此，假设的可能性 pθ(^r)如下。

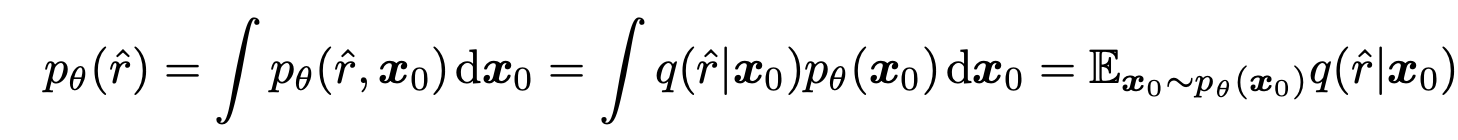
利用这些，物理正则化目标可表示如下

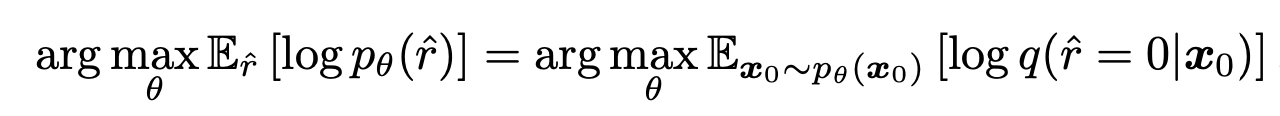
这意味着调整参数是为了使残差为零的概率最大化。作者指出，这是对物理信息神经网络误差函数的概率解释。

此外，在本研究中，除了上述误差函数外，还考虑了观测数据引起的误差函数。正如作者所指出的，这样做的效果是防止待估算函数的崩溃。举例来说，一个无处不为零的函数是一个满足特定类型控制方程的解，但在物理上毫无意义。我们需要观测数据的误差作为一种正则化项，以避免在寻找第一层时陷入这种非三维解的困境。加上观测数据的误差，目标函数定义如下

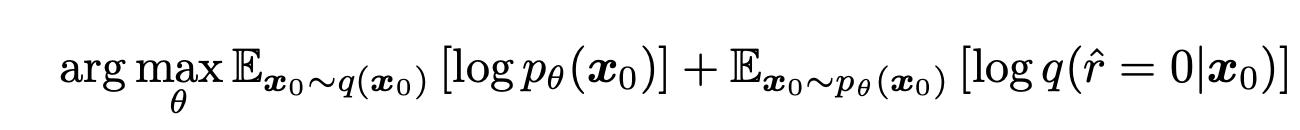
简化目标函数

对所有系列的去噪扩散模型施加零残差的正则化要求过于严格，有可能影响扩散模型的灵活性。因此，作者将正则化设计为在每一步都适当扩展。换句话说，他们将正则化设计为从 T 到 0 步的去噪过程中变得更强。下面是这方面的定义。图 1 还显示了去噪过程的 PIDM 示意图。

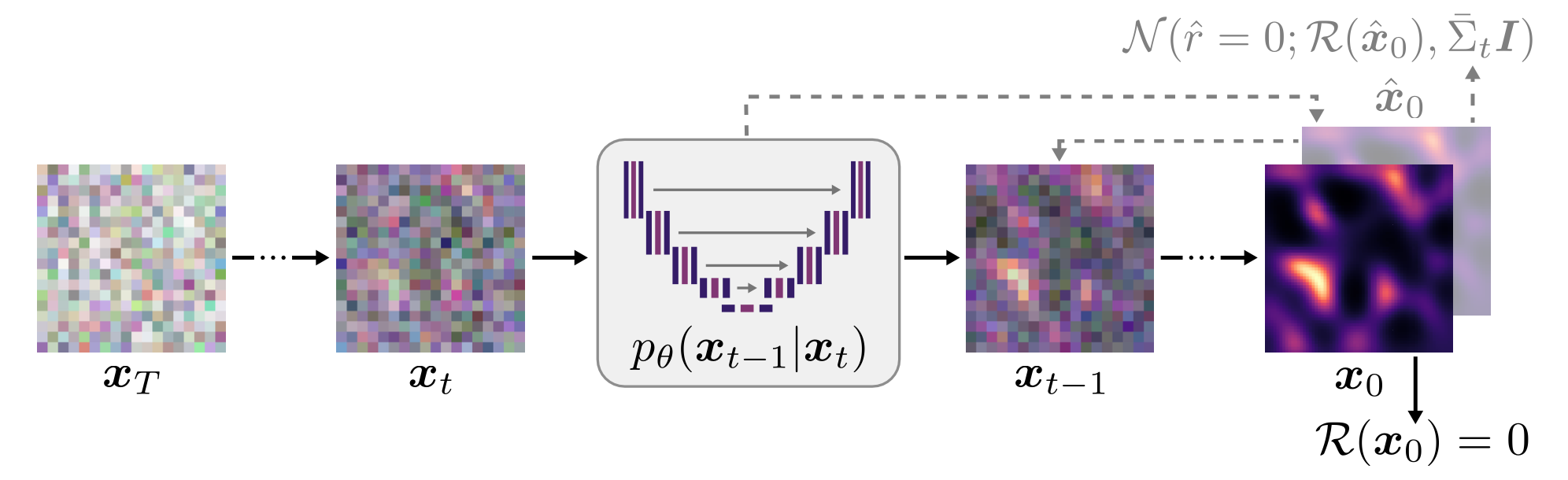
图 1：降噪过程中的 PIDM 原理图。

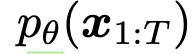
此外，考虑到目标函数的目的是近似，通过简化目标函数，最终可以得到以下目标函数

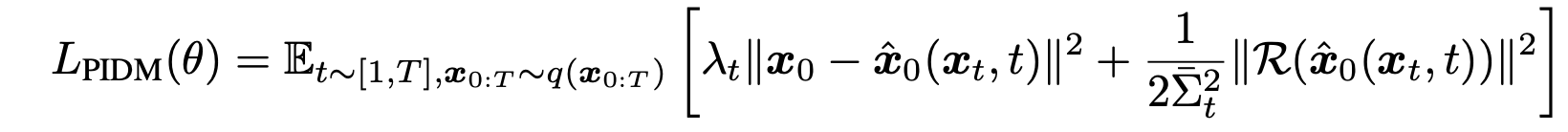
第一项是观测数据的误差函数，第二项是控制方程的误差函数。以上是 PIDM 的简要说明。

实验结果

在这项研究中，为了证明 PIDM 的有效性，我们进行了一些数值实验。在本评论中，将讨论多孔介质中二维达西流的一个示例问题，这是其中与物理相关性较高的一个问题。涉及的控制方程有

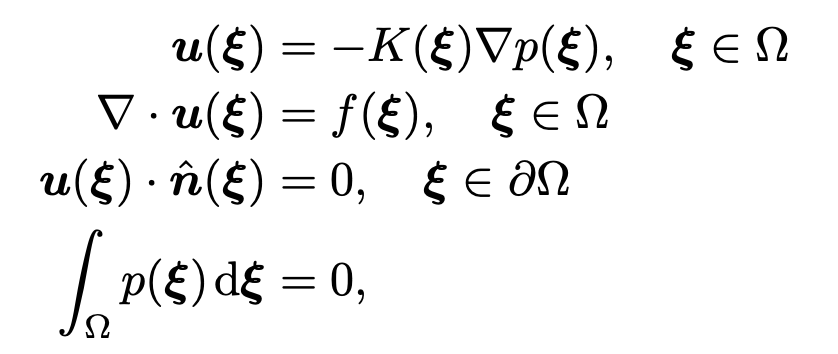
然而

是的。在这项研究中，准备了几个模型进行比较。(i) 从目标函数和数据中学习的扩散模型，(ii) 仅从目标函数和数据中学习但考虑残差信息作为指导的扩散模型（Phisics-guided diffusion），以及 (iii) 从目标函数和数据中学习但考虑残差信息作为指导的扩散模型（CoCoGen）。(iii) 在推理过程中使用残差但增加残差一阶修正的模型（CoCoGen）。本研究还考虑了在上述方程中生成介电常数和压力的模型。

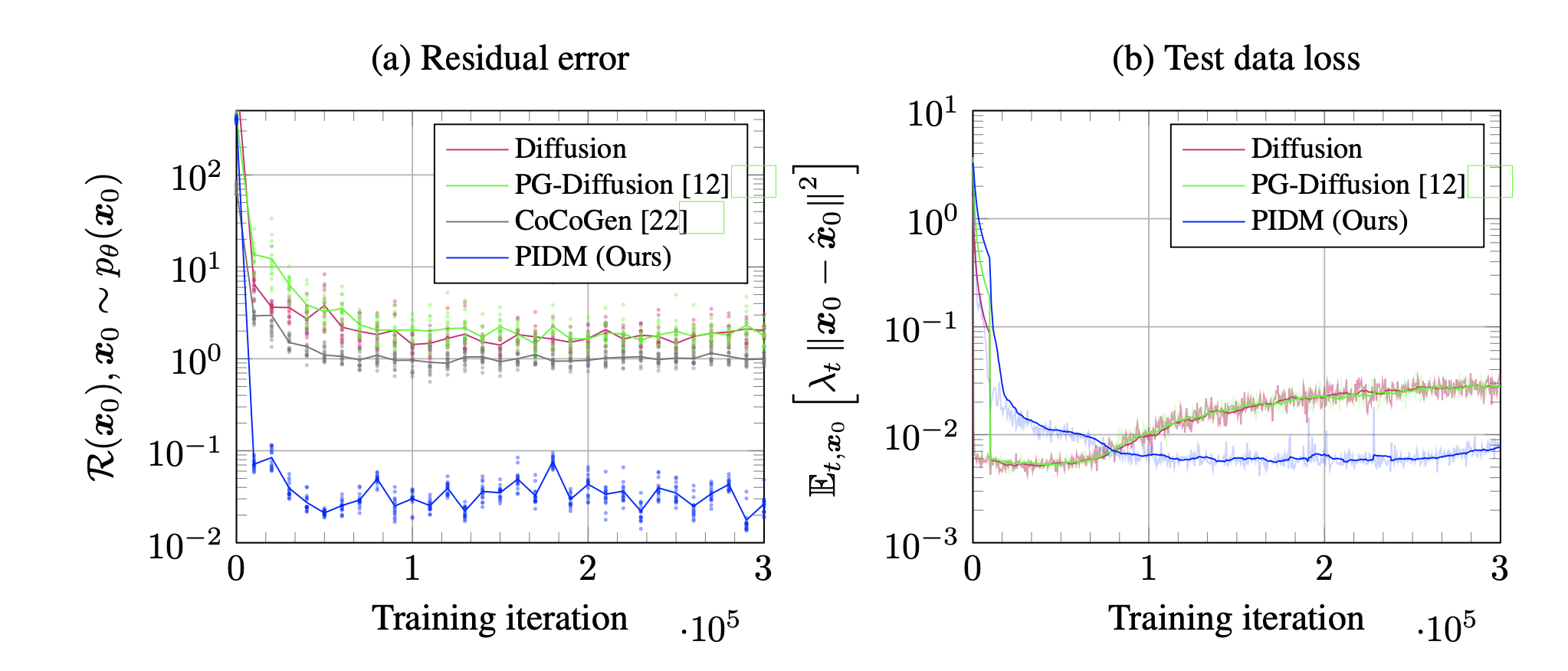
图 2：每个模型的学习过程可视化。

如图 2 所示，图 2 显示了学习各自模型和本研究提出的 PIDM 过程中误差函数的历史。从图 2(a)可以看出，随着残差误差的增大，PIDM 的效果提高了约两个数量级。此外，从图 2(b) 中的结果可以看出，随着学习的进行，传统方法的精确度会随着测试数据的增加而增加，预计会出现过拟合现象，而 PIDM 的物理正则化可以防止这种现象。这些结果表明，正则化项除了能提高准确度外，还能防止过度拟合。

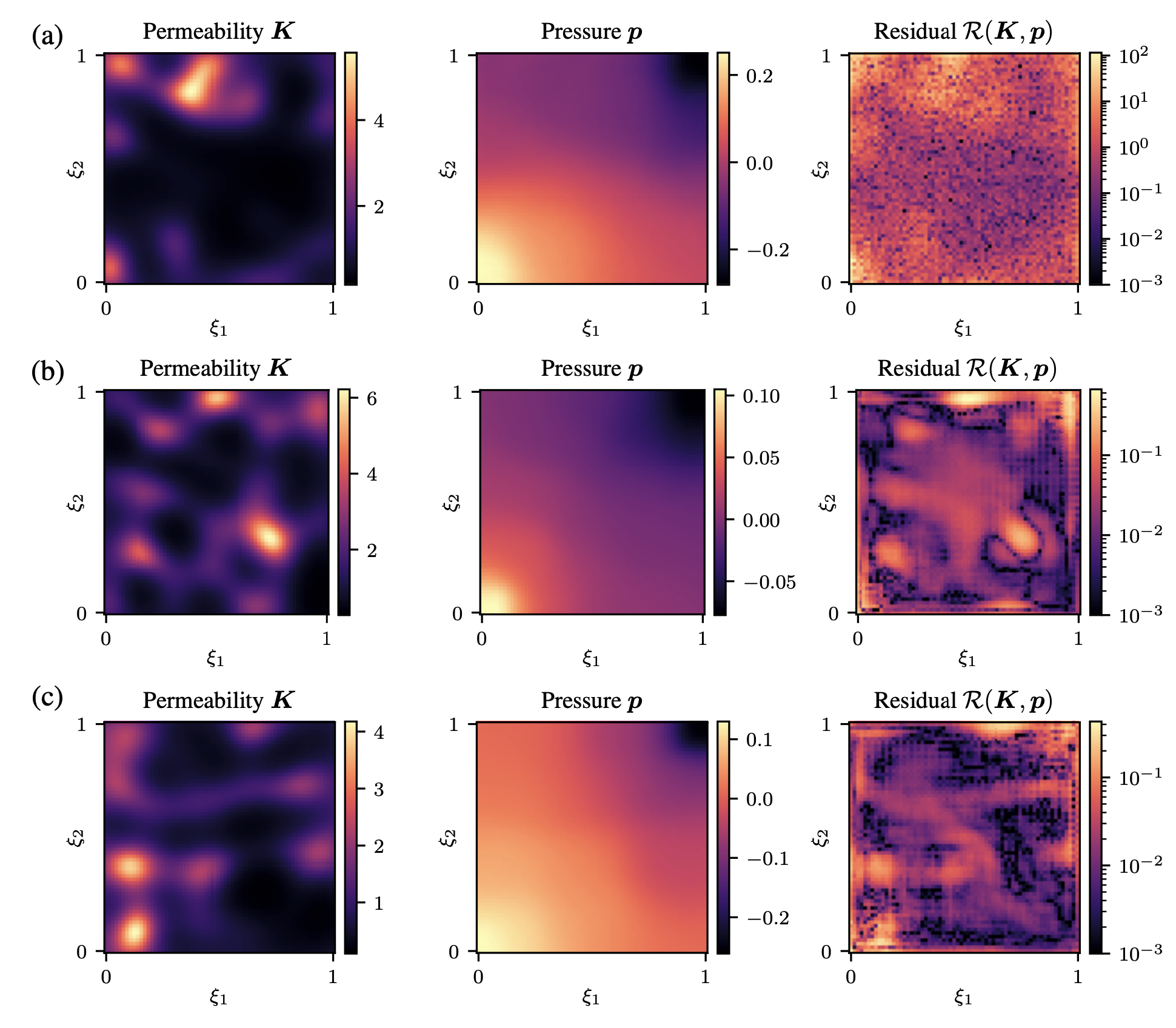
图 3.(a) 正常扩散模型给出的脆度和压力，(b) © PIDM 模型给出的脆度和压力。

图 3 还显示了正常扩散模型和 PIDM 得出的介电常数和压力的比较。图中还显示了这种情况下残差的空间分布。这一结果也证实了估算比正常扩散模型更准确，与图 2 中的结果一致。此外，图 3 中的(b)和©代表了不同的物理状态，表明 PIDM 可以代表多种状态，而不会陷入单一的解决方案。这些结果支持了 PIDM 的巨大潜力。

总结

在本研究中，我们从理论上推导出了添加了物理正则化项的扩散模型 PIDM，并通过数值实验证明了其性能。特别是，它允许直接对扩散模型施加物理正则化，而不是像以前的研究那样，在推理过程中 "固定 "潜变量。数值实验还表明，与常规扩散模型相比，PIDM 除了能将残差误差提高约两个数量级外，还能很好地避免过度拟合。随着自然科学领域对扩散模型的需求不断增加，本研究提供的理论基础有望在未来发挥重要作用。它有望在未来广泛应用于各种具体和不同的自然科学问题，并成为通用工具的基础。