这里是Themberfue
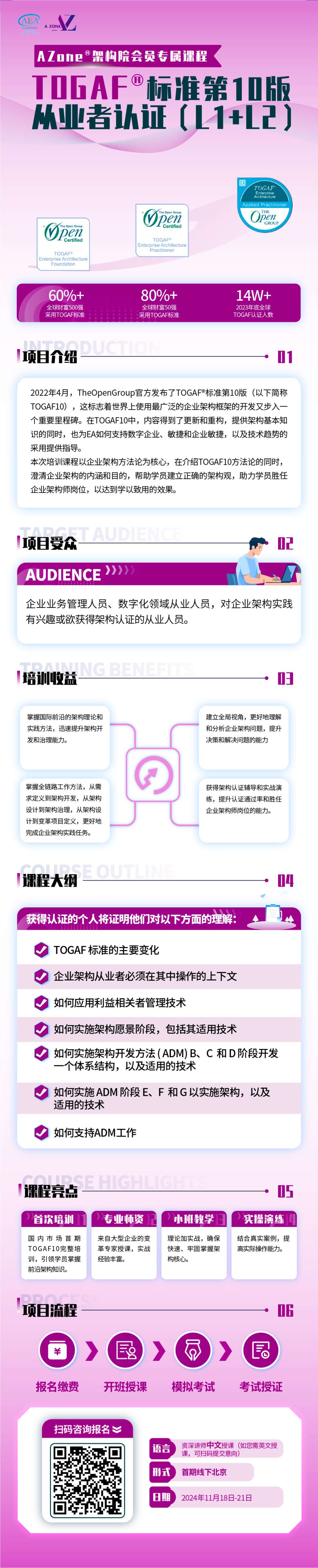
今天继续讲解经典算法 => 双指针算法
没看过上篇文章的小伙伴记得去看看哦😘
有效三角形的个数
题目链接:有效三角形的个数
题目解析

题目要求在该数组中任意选取三个数,看这三个数是否可以构成可以一个有效三角形。最后返回可以构成三角形的个数。
算法讲解
我们都知道,三角形的任意两条边的和都大于第三条边。利用这个性质。
所以,只要最大的那条边小于其他两条边的和,那么这个三角形就是有效的。
我们先对数组排序,保证其单调性。
先选取一个数组的最大数,也就是最后一位数,假设为 nums[i] 。
其次定义两个左右指针,假设为left, right,一个指向数组最左边,另一个指向最后一位数的前一位。
此时,选取出了三个数字。那么我们分情况讨论:
1.若 nums[left] + nums[right] > nums[i] 此时说明可以构成一个有效的三角形 => 如果此时固定right的位置,让left向右走,你会发现,由于数组是单调递增的,所以left所指向的值只会不断增大,不会减小,所以 nums[left] + nums[right] > nums[i] 恒成立,所以left向左走没有意义,此时的有效三角形的即为 right - left 也就是这两个指针间隔的数字个数。随后让 right向左走以减小 right所指向的值,继续判断。
2.若 nums[left] + nums[right] <= nums[i] 此时说明不可以构成一个有效的三角形,要让条件尽可能成立,只能是 left向右走,也就是让其指向的值尽可能增大。
编写代码
class Solution {
public int triangleNumber(int[] nums) {
Arrays.sort(nums);
int count = 0;
for (int i = nums.length - 1; i > 1; i--) {
int left = 0;
int right = i - 1;
while (left < right) {
if (nums[left] + nums[right] > nums[i]) {
count += right - left;
right--;
} else {
left++;
}
}
}
return count;
}
}查找总价格为目标值的两个商品
题目链接:查找总价格为目标值的两个商品
题目解析
总所周知,leetcode的简单题不一定是简单题,但这题确实是简单题,就是求两数之和。
算法讲解
这题用枚举也当然可以写,本质上其实也是双指针,但是时间复杂度为O(n^2),算是比较高的了。
题目明确说了,数组是按升序排序的,那么我们可以利用这一特点。
定义两个指针,一个指向最左边,一个指向最右边。
现在将这两个指针所指向的元素的和与 target 比较 => 那么出现了两种情况:
若是 price[left] + price[right] > target => 那么就需要操作一个指针的移动了,如果是left移动,根据升序数组,它只会增大,不会减小,那么就永远不可能达到 target 了,所以需要right 指针移动。
若是 price[left] + price[right] < target => left指针移动即可。
若是 price[left] + price[right] = target => 返回 left 和 right 指向的元素即可。
编写代码
class Solution {
public int[] twoSum(int[] price, int target) {
int left = 0;
int right = price.length - 1;
while (left < right) {
if (price[left] + price[right] > target) {
right--;
} else if (price[left] + price[right] < target) {
left++;
} else {
return new int[]{price[left], price[right]};
}
}
return new int[0];
}
}三数之和
题目链接:三数之和
题目解析

寻找三个下标不同的数字,这三个数字的和为0,既满足条件,但这题是要找到所有符合的。
算法讲解
与讲解的第一题类似,由于题目并没有要求返回数组的下标,所以我们先对数组进行排序,利用其单调性解题。
我们先在下标为0的位置选取该数字记为 nums[i]。
定义两个指针,left 指向 i + 1的位置,right 则指向数组最后的位置。
现在选取了三个数字,我们不用真正的将这三个数字加起来判断其是否为零(当然这样也行),如果 nums[left] + nums[right] 的结果为 nums[i] 的相反数,那么自然的,这三个数之和一定为零。
代码优化以及细节:
由于数组中可能存在重复数字,我们在对 i++,left++,right-- 时,可以跳过重复的数字,避免重复计算。
如果此时 nums[i]以及大于零了,就说明其之后的数字就一定大于零,所以 nums[left] + nums[right] 也不可能 和 nums[i] 互为相反数了。
编写代码
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> ret = new ArrayList<>();
int i = 0;
while (i < nums.length) {
int left = i + 1, right = nums.length - 1;
while (left < right) {
if (nums[left] + nums[right] < -nums[i]) {
int tmpLeft = nums[left];
left++;
while (left < right && nums[left] == tmpLeft) {
left++;
}
} else if (nums[left] + nums[right] > -nums[i]) {
int tmpRight = nums[right];
right--;
while (left < right && nums[right] == tmpRight) {
right--;
}
} else {
List<Integer> list = new ArrayList<>();
list.add(nums[i]);
list.add(nums[left]);
list.add(nums[right]);
ret.add(list);
int tmpLeft = nums[left], tmpRight = nums[right];
while (nums[left] == tmpLeft && nums[right] == tmpRight && left < right) {
left++;
right--;
}
}
}
if (nums[i] > 0) {
break;
}
int tmpI = nums[i];
i++;
while (i < nums.length && nums[i] == tmpI) {
i++;
}
}
return ret;
}
}四数之和
题目链接:四数之和
题目解析
与双数之和类似,现在需要选取四个数字,它们的和为 target,并且是选取所有符合条件的
算法解析
解法其实与三数之和类似,三数选取 nums[i]作为基准值,那么四数之和则需要 选取 nums[i]以及 nums[j] 作为基准值。
这里也不需要将这四个数相加判断其是否等于 target,只需要 nums[left] + nums[right] == target - nums[i] - nums[j] 即可。
代码优化以及细节处理和三数之和也是几乎一样。
编写代码
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> ret = new ArrayList<>();
int i = 0;
while (i < nums.length) {
int j = i + 1;
while (j < nums.length) {
int left = j + 1, right = nums.length - 1;
long aim = (long)target - nums[j] - nums[i];
while (left < right) {
if (nums[left] + nums[right] < aim) {
int tmpLeft = nums[left];
left++;
// 去重
while (left < right && nums[left] == tmpLeft) {
left++;
}
} else if (nums[left] + nums[right] > aim) {
int tmpRight = nums[right];
right--;
// 去重
while (left < right && nums[right] == tmpRight) {
right--;
}
} else {
ret.add(Arrays.asList(nums[left], nums[right], nums[i], nums[j]));
int tmpLeft = nums[left], tmpRight = nums[right];
// 去重
while (nums[left] == tmpLeft && nums[right] == tmpRight && left < right) {
left++;
right--;
}
}
}
int tmpJ = nums[j];
j++;
// 去重
while (j < nums.length && nums[j] == tmpJ) {
j++;
}
}
int tmpI = nums[i];
i++;
// 去重
while (i < nums.length && nums[i] == tmpI) {
i++;
}
}
return ret;
}
}好了,以上就是今天内容的全部讲解,如果有不懂的地方,随时私聊😘
我们下一个算法讲解见 => 滑动窗口😁