目录
- 前言
- 冒泡排序
- 快速排序
- Hoare版
- 前后指针版
- 优化
- 三数取中法
- 取随机数做基准值
- 小区间优化
- 快排非递归版

前言
对于常见的排序算法有以下几种:

下面这节我们来看交换排序算法。
冒泡排序
基本思想:
在待排序序列中,每一次将相邻的元素进行两两比较,将较大(升序)或者较小(降序)的数字往后走,每走完一轮,最大或者最小的数都会在最后面。
排序过程:
我们给一个要排序的序列,并想让其升序排序:
int arr[] = {5, 3, 9, 6, 2, 4, 7, 1, 8};


我们每排完一趟就会有在剩余待排序序列中的最大值被放到最后。
我们就可以用两层循环来控制。
外循环:控制冒泡排序的趟数,或者叫做轮数,由上图可以看出有n个数,则要排n-1轮。内循环:控制每一轮排序时两两之间的比较,可以发现,随着轮数的增加,每排好一个数,两两之间的比较次数就会少一次。最开始的比较次数同样为n-1次。
由此我们可写得循环为:
for(int i = 0; i < n - 1; i++)
{
for(int j = 1; j < n - i; j++)//最开始的比较次数共n-1次
{
//......
}
}
完整代码:
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void BubbleSort(int* a, int n)
{
for(int i = 0; i < n - 1; i++)
{
for(int j = 1; j < n - i; j++)//最开始的比较次数共n-1次
{
if(a[i - 1] > a[i]
{
Swap(a[i - 1],a[i]);
}
}
}
}
排序代码已经结束了,但是我们通过第二个图可以发现,到后面已经有序了,但还是在进行判断冒泡,因此我们可以对上述程序进行改良:
多增加一个变量exchange = 0,如果它进行了排序,则exchange = 1,如果没有排序则exchange = 0,证明此时已经完成了排序,则直接跳出循环即可。
改良后的排序代码:
void BubbleSort(int* a, int n)
{
for(int i = 0; i < n - 1; i++)
{
int exchange = 0;
for(int j = 1; j < n - i; j++)
{
if(a[i - 1] > a[i]
{
exchange = 1;
Swap(a[i - 1],a[i]);
}
}
if(exchange == 0)//没有变化证明已经有序了,直接结束即可
break;
}
}
冒泡排序特性总结:
- 时间复杂度:
O(N^2^) - 空间复杂度:
O(1) - 稳定性:
稳定
快速排序
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序算法。
Hoare版
基本思想:
1.任取待排序元素序列中的的某元素作为基准值,并定义两个指针分别指向序列的开始和结尾,遍历该数据,根据规则进行交换以及指针的移动,直至两指针相遇。
2.此时将基准值与两指针相遇指向的值交换,此时基准值就到了正确的位置。
3.此时将该序列分成了左右两边,左边序列的数都比此基准值小,右边序列的数都比此基准值大。
4.再重复上述步骤,可将所有数排好。
其实也就是递归。
当说可能不太清楚,下面我们通过图来解释:


总体代码如下:
void Swap(int* px, int* py)
{
int tmp = *px;
*px = *py;
*py = tmp;
}
void QuickSort1(int* a, int left, int right)
{
if (left >= right)//递归结束条件,如果区间中只有一个值或不存在
return;
int begin = left, end = right;
int key = left;//用的都是下标
while (left < right)
{
while (left < right && a[right] >= a[key])//让右指针先走,右指针要找到比a[key]小的
right--;
while (left < right && a[left] <= a[key])//左指针后走
left++;
Swap(&a[left], &a[right]);
}
//此时left和right相遇
Swap(&a[left], &a[key]);
//更新key的下标
key = left;
//分了左右两个区间[begin, key-1] key [key+1, end]
//递归,使剩余区间都按上面操作
QuickSort1(a, begin, key - 1);
QuickSort1(a, key + 1, end);
}
拓展:我们最后是让left和right相遇所指向的值与基准值交换,我们是要升序排序,这也就是二者相遇指向的值必定小于基准值,这是为什么呢?
原因如下:
- 很重要的一点就是
右边先走保证的,二者相遇无非就两种情况,一种是left遇上right,另一种就是right遇上left。下面来分别讨论: left遇上right:right先走,当right走到比key小的值就停了下来,left再走,要找比key大的值,但是它找不到,一直走就会和right想遇,此时相遇所指向的值就比key小。right遇上left:如果第一轮二者就相遇:right先走,right没有找到比key小的值,就一路左移,遇到left,也就是key的位置。right遇上left:二者第一轮以后相遇,此时二者是经过第一轮的交换,也就是left此时指向的位置比key小,right先走,它没有找到比key小的值,一直左移就和left相遇,此时指向的还是比key小的值。
因此,只要保证让right先走,在升序时就能保证相遇时所指向的值小于基准值。
前后指针版
给定两个指针,一个prev指向key位置处,另一个cur指向prev的下一个位置。
基本思想:
- a[cur] >= a[key],++cur;
- a[cur] < a[key],++prev,交换prev和cur位置的值,++cur;

通过上述步骤可以发现,prev和cur之间的数都是比基准值大的,也就是通过不断交换,将比基准值大的数都被放在了prev和cur之间,则当cur走到最后时,二者之间就都是比cur大的了。
后面的同样根据上述步骤重复进行即可得到。
具体代码如下:
void QuickSort2(int* a, int left, int right)
{
if (left >= right)//递归结束条件,如果区间中只有一个值或不存在
return;
int prev = left, cur = left + 1;
int key = left;
while (cur <= right)
{
if (a[cur] < a[key])
{
++prev;
Swap(&a[prev], &a[cur]);
cur++;
}
else
cur++;
}
Swap(&a[key], &a[prev]);
key = prev;
//分了左右两个区间[begin, key-1] key [key+1, end]
//递归,使剩余区间都按上面操作
QuickSort2(a, left, key - 1);
QuickSort2(a, key + 1, right);
}
优化
由于快排是一种递归式的排序,时间复杂度和堆排差不多,都是O(NlogN)。但如果序列有序或者接近有序时,此时时间复杂度就会高很多,就几乎达到了O(N^2^)。这是取基准值一直取的第一个导致的。

因此解决办法就是在每次对基准值的查找不要一直是第一个。下面有几种方式:
三数取中法
基本思想:
在需要排序的序列中,找到最左边,最右边以及中间的三个数,将这三个数比较大小,取中间大的数字。并将此数字作为基准值,然后将其与最左边的数交换,使基准值保持在最左边的位置,便于后续遍历。
适用序列:有序或接近有序的情况。
核心:找到中间大的数。

具体代码如下:
int GetMid(int* a, int left, int right)//三数取中
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] < a[right])//a[mid]>=a[right]
return right;
else
return left;
}
else//a[left]>=a[mid]
{
if (a[right] < a[mid])
return mid;
else if (a[left] < a[right])//a[mid]<=a[right]
return left;
else
return right;
}
}
void QuickSort1(int* a, int left, int right)
{
if (left >= right)//递归结束条件,如果区间中只有一个值或不存在
return;
int begin = left, end = right;
//找到中间的数
int mid = GetMid(a, left, right);
//与最左边的值交换
Swap(&a[mid], &a[left]);
int key = left;//用的都是下标
//......
}
取随机数做基准值
我们不想每次都取最左边的值做基准值,那我们在[left, right]此区间内找随机值即可。思想还是比较简单的。
具体代码如下:
void QuickSort1(int* a, int left, int right)
{
if (left >= right)//递归结束条件,如果区间中只有一个值或不存在
return;
int begin = left, end = right;
//要使得所取的随机数在[left, right]区间中
int randi = rand() % (right - left +1);
//left不一定为0
randi += left;
//与最左边的值交换
Swap(&a[randi], &a[left]);
int key = left;//用的都是下标
//......
}
小区间优化
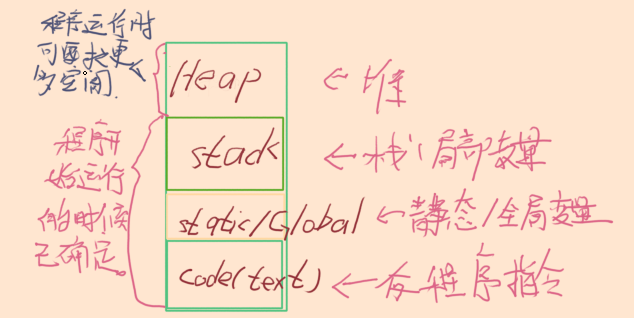
正如堆所示,最后两到三层的节点数量占了整个的百分之八十左右,此时我们用递归消耗是比较大的,因此我们可以在最后的区间内使用插入排序。减少消耗。
代码如下:
void QuickSort1(int* a, int left, int right)
{
if (left >= right)//递归结束条件,如果区间中只有一个值或不存在
return;
int begin = left, end = right;
//小区间优化
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
}
else
{
//要使得所取的随机数在[left, right]区间中
int randi = rand() % (right - left + 1);
//left不一定为0
randi += left;
//与最左边的值交换
Swap(&a[randi], &a[left]);
/*int mid = GetMid(a, left, right);
Swap(&a[mid], &a[left]);*/
int key = left;//用的都是下标
//.........
QuickSort1(a, begin, key - 1);
QuickSort1(a, key + 1, end);
}
}
快排特性总结:
- 时间复杂度:
O(NlogN),每趟确定的元素呈现指数增长。 - 空间复杂度:
O(logN),递归是需要用的栈空间 - 稳定性:
不稳定
快排非递归版
将递归转化为非递归,可以借助循环来解决。
我们可以借助栈后进先出的思想来模拟递归区间的使用。
如图:

判断是否入栈:看区间是否有两个以上的值,如果只有一个值就没有必要入栈排序了。
判断while循环结束的条件:栈不为空则继续,为空则结束。
代码如下:
#include"Stack.h"
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);//初始化栈
STPush(&st, right);//先进右
STPush(&st, left);//再进左
while (!STEmpty(&st))//循环条件是栈不为空
{
int begin = STTop(&st);//左是后进的,所以取出来就是begin
STPop(&st);
int end = STTop(&st);
STPop(&st);
// 单趟
int keyi = begin;
int prev = begin;
int cur = begin + 1;
while (cur <= right)
{
if (a[cur] < a[key])
{
++prev;
Swap(&a[prev], &a[cur]);
cur++;
}
else
cur++;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
// [begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)//如果区间有两个值以上则入区间
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
if (begin < keyi-1)
{
STPush(&st, keyi-1);
STPush(&st, begin);
}
}
STDestroy(&st);//要记得把栈销毁
}
感谢大家观看,如果大家喜欢,希望大家一键三连支持一下,如有表述不正确,也欢迎大家批评指正。