530.二叉搜索树的最小绝对值差
题目:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode)
给你一个二叉搜索树的根节点
root,返回 树中任意两不同节点值之间的最小差值 。差值是一个正数,其数值等于两值之差的绝对值。
示例 1:
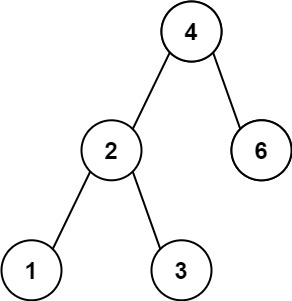
输入:root = [4,2,6,1,3] 输出:1
递归法
直观思路就是,中序遍历二叉树,暴力一点就是新开一个有序数组存储这些值,再求差。本题使用双指针法。 然后求相邻两个节点之间的差值就可以了。
会做上一题,这题也会做了。
class Solution {
private:int result=INT_MAX;
TreeNode*pre=NULL;
void traversal(TreeNode*cur)
{
if(cur==NULL)return;
traversal(cur->left);//左
if(pre!=NULL)//中
{
result=min(result,cur->val-pre->val);//求相邻两个数的最小差值
}
pre=cur;
traversal(cur->right);//右
}
public:
int getMinimumDifference(TreeNode* root) {
traversal(root);
return result;
}
};迭代法
使用栈来模拟中序遍历过程。
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
stack<TreeNode*>st;
TreeNode*pre=NULL;
TreeNode*cur=root;
int result=INT_MAX;
while(cur!=NULL||!st.empty())
{
if(cur!=NULL)//一路遍历到左子树的底,依次入栈
{
st.push(cur);//左
cur=cur->left;
}
else
{
cur=st.top();
st.pop();//中
if(pre!=NULL)
result=min(result,cur->val-pre->val);
pre=cur;//保存当前值
cur=cur->right;//右
}
}
return result;
}
};501.二叉搜索树中的众数
题目:501. 二叉搜索树中的众数 - 力扣(LeetCode)
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
例如:
给定 BST [1,null,2,2],
返回[2].
提示:如果众数超过1个,不需考虑输出顺序
如果是非二叉搜索树,就要用到哈希表,具体步骤是:遍历整棵树,map统计出现频率和对应的值。再给出现频率value排序,最后取出高频数就可。
是二叉树搜索时树,用中序遍历就是有序的。和上题一样双指针法遍历,只不过在统计比较频率和求最大频率集合(众数可以不只一个)上用点技巧。
递归·法
class Solution {
private:
TreeNode*pre=NULL;
int count=0;
int maxcount=0;
vector<int>result;
void searchBST(TreeNode*cur)
{
if(cur==NULL)return;
searchBST( cur->left);//左
//中
if(pre==NULL)count=1;
else if(pre->val==cur->val)count++;//如果和前一个数相同,则频率+1
else count=1;//重置为1。所以不能直接初始值为1
if(count==maxcount)result.push_back(cur->val);
if(count>maxcount)
{
maxcount=count;
result.clear();//清空
result.push_back(cur->val);//更新众数
}
pre=cur;
searchBST(cur->right);//右
return;
}
public:
vector<int> findMode(TreeNode* root) {
result.clear();
searchBST(root);
return result;
}
};迭代法
用栈来模拟中序遍历迭代写法,中的处理逻辑一点没变,和上题一模一样,只是换了一个写法。
class Solution {
public:
vector<int> findMode(TreeNode* root) {
stack<TreeNode*>st;
TreeNode*pre=NULL;
TreeNode*cur=root;
int count=0;
int maxcount=0;
vector<int>result;
while(cur!=NULL||!st.empty())
{
if(cur!=NULL)
{
st.push(cur);
cur=cur->left;//左
}
else
{
cur=st.top();
st.pop();
//中
if(pre==NULL)count=1;
else if(pre->val==cur->val)count++;//如果和前一个数相同,则频率+1
else count=1;//重置为1。所以不能直接初始值为1
if(count==maxcount)result.push_back(cur->val);
if(count>maxcount)
{
maxcount=count;
result.clear();//清空
result.push_back(cur->val);//更新众数
}
pre=cur;
cur=cur->right;//右
}
}
return result;
}
};小总结,上两题类似的地方挺多的。都是使用中序遍历,只是中的处理逻辑稍有不同。总体还是简单的,然后难的来了。
236.二叉树的最近公共祖先
题目:236. 二叉树的最近公共祖先 - 力扣(LeetCode)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
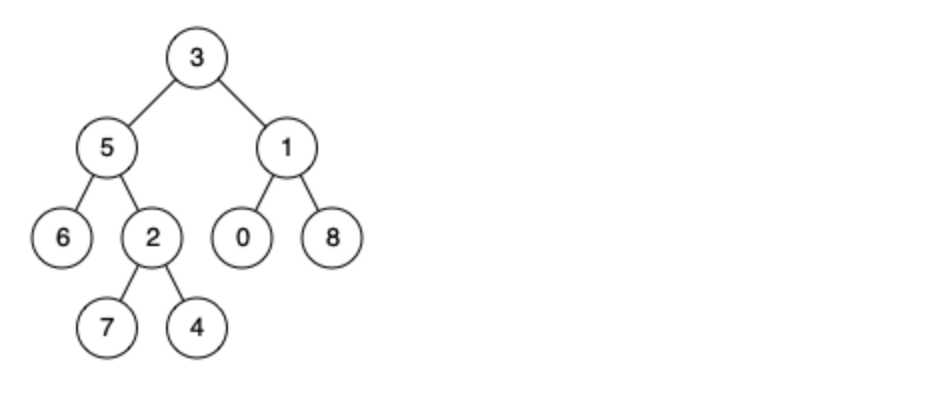
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
思路:
后序遍历就是一个回溯过程,这样就可以自底往上查公共祖先。
首先情况一,找到一个节点,左子树有p右子树有q或者左子树有q右子树有p。

判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。 (题目说pq不同且一定存在)
情况二就是p或q本身就是公共祖先。

但是情况一处理的时候也包含了情况二。
如:当 p 是 q 的祖先时,代码中的 if (root == q || root == p) 判断会保证函数直接返回 p,无需继续递归。
3
/ \
5 1
/ \
6 2
- 假设
p = 5,q = 6,即p是q的祖先。 - 当递归到
root = 5时,会触发if (root == p)的条件,直接返回p,即节点5。 - 由于
p是q的祖先,最近的公共祖先就是p本身,整个算法就会正确返回5。
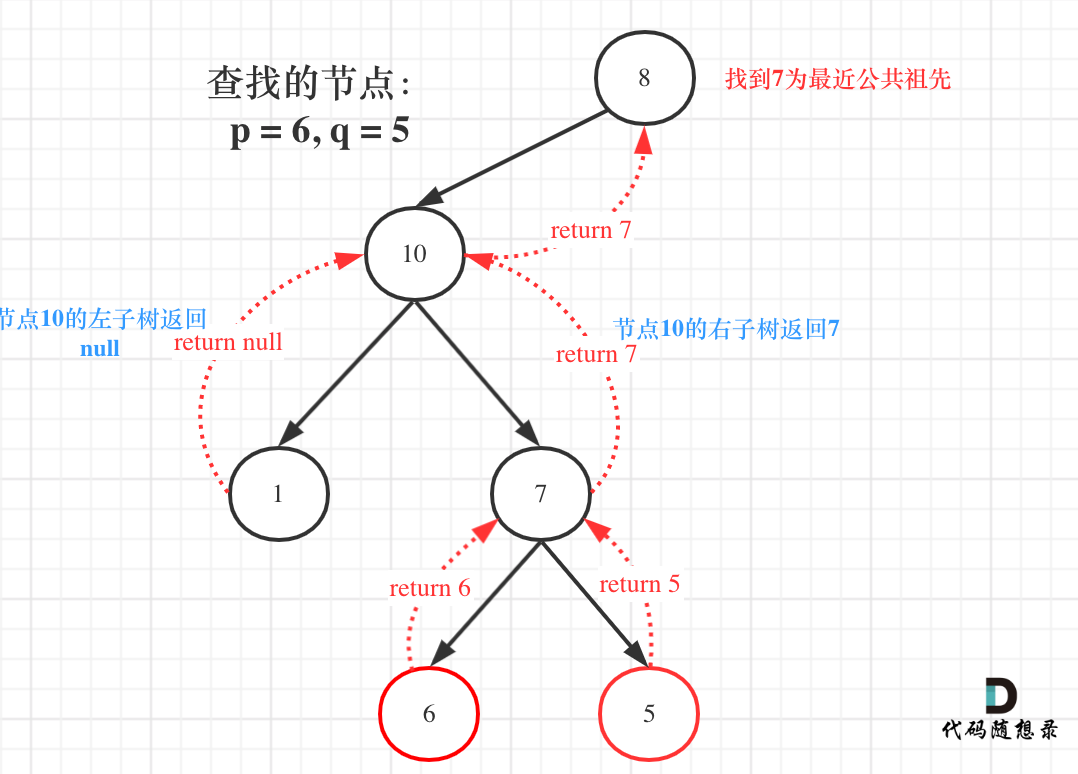
注意就是递归的返回值问题。如果是搜索一条边那么就不需要返回值。如果要搜索整棵树那么就需要left和right接住返回值。而本题需要遍历整棵树是因为后序遍历(左右中)的特性,需要left和right的逻辑处理完成后(中)才能返回值。
还有一点如图就知道了。
如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,反之依然。
如图:
递归法
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root==q||root==p||root==NULL)return root;
TreeNode*left=lowestCommonAncestor(root->left,p,q);//左
TreeNode*right=lowestCommonAncestor(root->right,p,q);//右
if(left!=NULL&&right!=NULL)return root;//中,如果 left 和 right 都不为空,说明 p 和 q 分别在 root 的左右子树中,因此 root 是它们的最近公共祖先,返回 root。
if(left==NULL&&right!=NULL)return right;//如果 left 为空,而 right 不为空,说明两个节点都不在左子树中,且右子树中找到了一个有效结果,因此返回 right。
else if(left!=NULL&&right==NULL)return left;//同上
else
return NULL;//两边都为空,证明两棵树都没有p和q的存在。
}
};