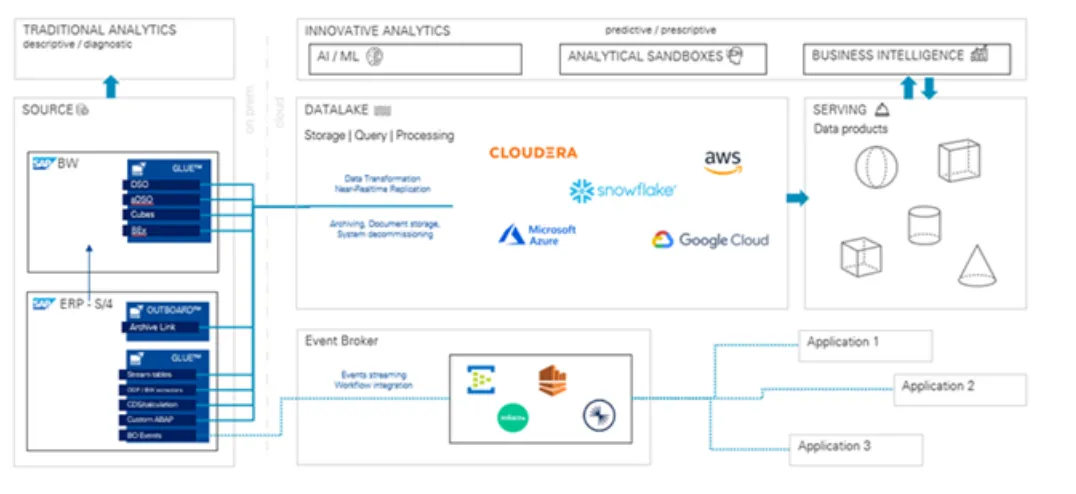
齐次坐标是一种在计算机图形学、计算几何和机器人学中广泛使用的坐标表示方法。它通过引入额外的维度，将传统的欧几里得坐标转换为齐次坐标，从而简化一些数学运算，尤其是在变换（如平移、旋转和缩放）时。

齐次坐标的定义

对于二维空间中的点(x,y)，其齐次坐标可以表示为：

其中w 是一个非零的标量。通常，我们选择 w=1 来恢复到欧几里得坐标。

在三维空间中，齐次坐标的表示为：

同样，w 也可以是任何非零值。

齐次坐标的优点

统一变换：齐次坐标使得平移、旋转和缩放等线性变换可以用矩阵乘法统一处理。
点与无穷远点的表示：齐次坐标可以用来表示无穷远点，这在某些几何应用中非常重要。
简化方程：许多几何变换和投影操作在齐次坐标下可以用简单的矩阵形式表达。

变换示例

1. 平移变换
   二维空间中的平移变换可以表示为：
   

2. 旋转变换
   二维空间中的旋转变换可以表示为：
   

总结

齐次坐标是一个强大的工具，在计算机视觉和几何处理中起着关键作用。它提供了一种简洁的方式来处理各种几何变换，并且方便了点与无穷远点的表示。