GAMES101（21~22节，动画和仿真）

news2024/9/29 1:31:28

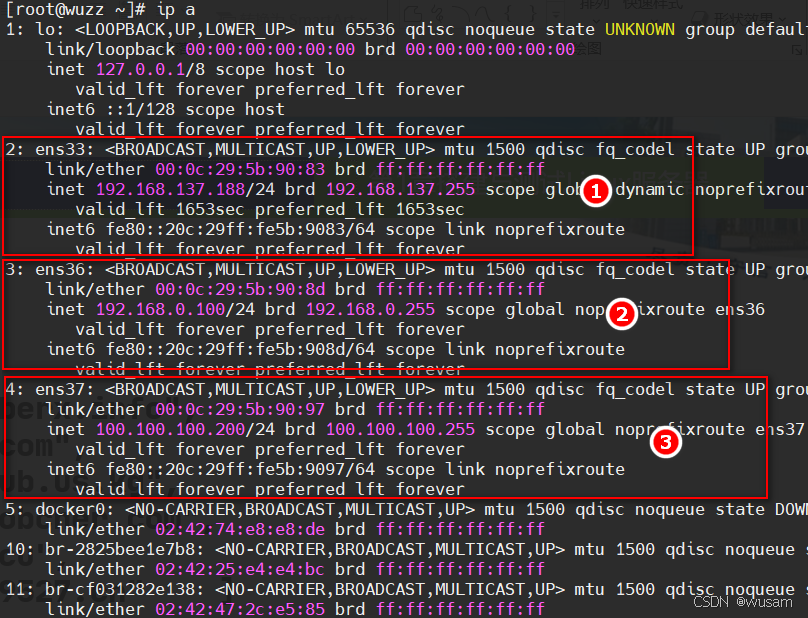
Animation

关键帧

动画和几何（曲线）相关

物理模拟/仿真

牛顿第二定律：F = ma

需要清楚网格间相互作用力，也需要把物理仿真和渲染分为两部来看，例如布料模拟，流体模拟

mass spring system质点弹簧系统

一个基本单位时一个弹簧，两个质点

推导受力分析

胡克定律（Hooke's Law）：ks劲度系数(取决于弹簧的材料) * 单位向量（方向）*（||b-a|| - l ）原始长度（形变量）

根据力的相互作用，a点受到b方向的力，b点受到往a方向的力，又因为当前静止状态，也就是作用力 == 反作用力，b点受到往a方向的力 == a点受到b方向的力的反作用力

其实总的受力应为这样的平衡关系，ab都有弹力势能和拉力

这时当b松手，b的拉力消失，b点受力不再平衡，a对b产生的弹力势能，转换为动能，

没有其他力影响，因而总能量不变，动能势能不断相互转换，b永远不会停止

一阶导数，在物理模拟中在上方 · 点号，二阶用 ·· 表示

对于路程/时间函数的一阶导数为速率，二阶导数为加速度

那么为了让b停止，需要加摩擦力，和b导数-.>b的速度的方向相反，其中kd依旧是劲度系数

但是这样会让所有运动都停止，假设ab同时被拉开，并且保持相对静止，同时向右运动，这时我为ab同时添加f摩擦力，因为根据上面的公式f和速度方向相反，也就是左方向，那么就会导致ab停止，但是ab的相对拉开的状态没有改变

这样是不符合我们的期望，我们期望，b可以在左右弹的过程逐渐停止，可是当同时ab运动时，上述并不能让ab恢复弹簧的原长度，仅能让ab不再向右移动

那么如何让ab依旧保持向右移动，并且ab逐渐恢复弹簧的原长度呢？

负号（相反），单位向量a->b，b导数（速度） - a导数（速度）,单位向量a->b

首先前两个，浮点 * 向量 = b->a得到的依旧是向量

后两个相乘，得到浮点，v向量 * 单位向量， = ||v|| costheta

假设b相对a向右弹，那么b的速率>a的速率，且为正值，cos = 1，fr即取相反值向左
假设b相对a向左弹，那么b的速率>a的速率，且为负值，cos = -1，fr即取相反值向右

这里为什么要乘以单位向量？

假设b相对于a圆周运动，ba速度虽然不同，但弹簧的长度没有改变，因为ab的相对弹力没有改变，不应该在内部施加摩擦力（圆周运动不应该有恢复原状的返回力，只有在ab方向上的速度改变，才应在内部施加摩擦力），

假如没有单位向量，那么获得的fr摩擦力向量就是速度的反向，考虑上述不应有摩擦力的情况，因此，当点乘单位向量b->a，会根据向量的夹角cos，当为90度，结果为0 ，即没有摩擦力

也就是第一个单位向量，保证了结果是向量，第二个单位向量，保证了正确的摩擦力结果

模拟

模拟一个布，不应该受到形变的影响，比如延对角线拉扯（通过蓝线），延某方向弯折，通过（较弱红线）

single particle simulation单粒子模拟

单粒子模拟：指对单个粒子运动轨迹的计算

假设知道初始位置，和每一刻的速度（矢量），那么它的新的位置很容易计算，但是我们根本不可能知道每一刻的速度

假设在速度场模拟粒子运动轨迹

速度场：在任意时刻t和位置x，都有对应的速度v(x,t)，也就是相当于函数

dx / dt 导数（切线）即速度，导数为瞬时速度

常微分方程

方程的形式有很多。代数方程是指含有未知数的等式；而微分方程，是指含有未知函数及其导数的等式。代数方程的解是常数，而微分方程的解是函数。

如果函数只有一个自变量的微分方程称为常微分方程（ordinary differential equation，ODE）。
如果函数含有两个或者多个自变量的微分方程称为偏微分方程（partialdifferential equation，PDE）。

此外，微分方程也可以根据阶数来分类：最高阶导数是一阶导数，则称为一阶微分方程（first-order-equation）；最高阶导数是二阶导数，则称为二阶微分方程（second-order-equation）。