编者按：

为提高最后一公里配送的效率，本文将客户激励与不确定的路线决策相结合，建立了一个两阶段随即规划问题，并开发了一种精确式的分支定界算法进行求解。

摘要：

为了提高最后一公里配送的效率，零售商可以通过激励措施引导客户从上门配送转向自提点配送以降低成本。然而，客户是否接受这一激励并选择自提点配送通常是不确定的。这种情况下就出现了一个新的最后一公里配送问题，该问题将客户激励和不确定的路线决策结合在一起。作者因此将该问题建模为一个两阶段随机规划问题。在第一阶段，零售商决定向哪些客户提供激励。然而，客户对激励的反应是随机的：他们可能接受优惠并转向自提点配送，或者拒绝优惠并坚持上门配送。在第二阶段，当客户的最终配送选择确定后，车辆路线将被规划，并根据客户的选择提供服务。作者开发了一种精确的分支定界算法，并提出了几种启发式方法以提高算法的可扩展性。相较于行业中常用的不使用激励或向所有客户提供激励的方法，这些算法能够平均降低4%–8%的最后一公里配送成本。

关键词：最后一公里配送问题、两阶段随机规划、客户偏好

1. 引言

疫情推动了零售业对上门配送的需求增长，但这一需求的时效准确性要求对零售商来说是重大挑战。为此，零售商引入了创新的配送机制，如自提点配送。这种模式通过订单整合提升配送效率，同时为客户提供了比上门配送更灵活的选择。尽管自提点配送具有潜在优势，但吸引客户选择这种配送方式仍存在困难，大部分客户更偏好上门配送。为解决此问题，作者提出通过货币激励引导客户从上门配送转向自提点配送。然而，由于客户可能拒绝激励继续选择家庭配送，零售商必须权衡激励成本与配送路线的成本，制定有效的激励政策。

该问题类似于ring star问题（RS）（Labbé et al. 2004），其目标是设计一条访问网络中部分节点的路线，并将未访问节点的需求以一定成本分配给已访问节点。在本文中，作者在此基础上引入了随机性的概念，即Decision-dependent ring star （DDRS）问题，每个客户根据零售商提供的激励政策，都有一定的概率发生从上门配送到选择自提点配送的选择转变。作者主要在以下三个方面分析此问题：

1. 引入新颖的DDRS模型，构建为一个两阶段随机整数规划问题。
2. 开发了精确的分支定界（B&B）算法，优化解决最多19名客户和5个自提点的实例，
3. 提出了启发式变体方法以解决最多50名客户和5个自提点的实例问题。

2. 模型描述

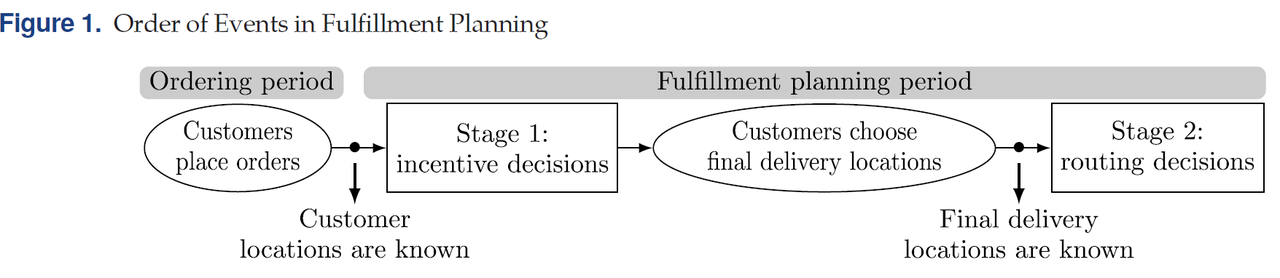
这个问题涉及一家在线零售商实施货币激励措施，以引导客户从选择送货上门转向选择自提点取货。该过程如Figure 1所示，首先是客户在截止时间前下单并输入其家庭住址以便开始订单履行规划。一旦所有客户的地址都确定，订单履行规划便开始。在此过程中，零售商首先会向选定的部分客户提供激励措施（如运费折扣），让他们选择将包裹送到最近的自提点，而不是送到家中，以节省路线成本。在本文中，作者假设零售商为客户提供一个单一的（最近的）自提点选项来简化决策过程。

因此，订单履行规划的第一阶段决策是制定激励政策，确定哪些客户会被提供到最近自提点的激励。客户随后可能会拒绝或忽略该激励，坚持选择送货上门，或者接受激励并切换到自提点取货，直到开始路线规划的截止时间。一旦所有客户确定了最终的送货地点，零售商就会规划送货路线，这构成了订单履行规划的第二阶段决策。送货路线必须包括选择自提点取货的客户以及剩余选择送货上门的客户的家庭地址。零售商的目标是最小化总的预期履行成本，其中包括激励成本和路线成本。将上述描述转化为模型即为：

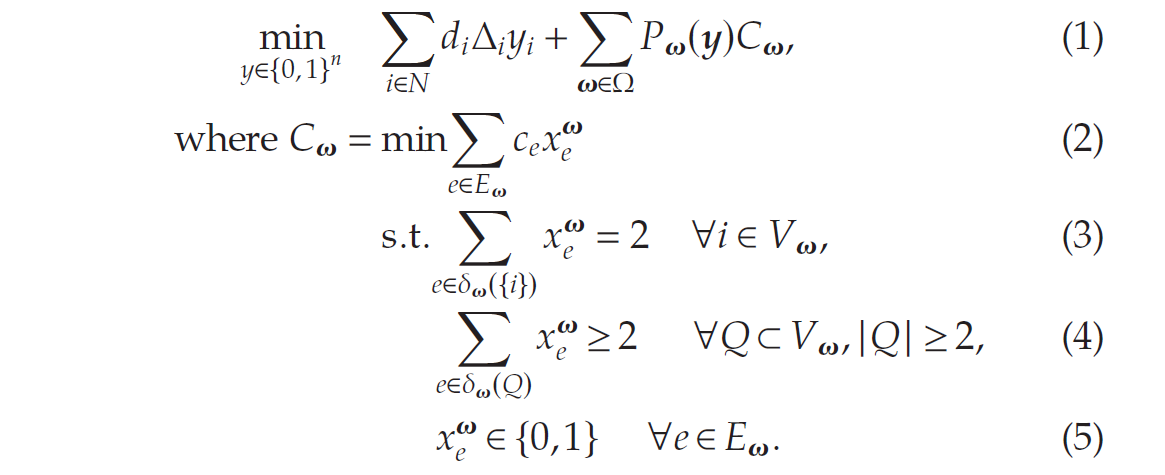
目标函数 (1) 最小化了在所有情景 $v\in \Omega$ 下的预期履行成本。与第二阶段情景 $v\in \Omega$ 相关的路线成本通过路线子问题 (2)–(5) 定义，其中对于某些顶点子集 $Q$，定义 δ v ( Q ) = { i , j ∈ E v ∣ i ∈ Q , j ∉ Q } \delta_v(Q) = \{{i,j} \in E_v| i \in Q, j \notin Q\} δv​(Q)={i,j∈Ev​∣i∈Q,j∈/Q} 以简化表达。方程 (2)–(5) 包括了一个标准的（对称）旅行商问题 (TSP) 的表述）。需要注意的是，虽然路线成本 $C_v$ 不依赖于第一阶段决策向量 $y$，但发生该成本的概率 $P_v(y)$ 是通过$y$ 决定的。

正如在前述随机规划模型中所观察到的，随着客户数量$n$的增加，模型规模呈指数级增长。存在$2^n$ 种不同的激励政策。此外，给定任何激励政策$y$，计算预期路线成本（方程 (1) 中的第二项求和）非常复杂，因为这涉及评估 $2^{{\sum }_{i\in N}{y}_i}$种不同情景下的成本和决策依赖概率，最坏情况下有$2^n$ 种不同的可能情景（即当所有客户都被提供激励时，$y_i=1,\forall i\in N$）。因此，随着激励数量的增加，每种独特选择情景$v$的概率$P_v(y)$会逐渐减小。因此，指望现成的求解器直接解决上述公式对于合理规模的问题是不现实的。结果是，必须评估大量情景才能合理近似任何给定激励政策下的预期路线成本。
为了解决这些问题，作者提出了一种精确的分支定界（B&B）算法，以高效解决由方程 (1)–(5) 定义的 DDRS 问题。

3. Branch-and-Bound 算法

Branch-and-Bound(B&B)算法通过在一个二分搜索树中隐式枚举激励政策来解决DDRS问题。B&B树中的每个分支节点代表一个部分政策，而每个叶节点代表一个完整政策。用向量$L=(l_i{)}_{i\in N}$来表示搜索树中的一个节点，其中 l i ∈ { 0 , 1 , # } l_i \in \{0, 1, \#\} li​∈{0,1,#}。如果向客户$i$提供激励，则$l_i=1$；如果不提供激励，则$l_i=0$；如果尚未对该客户做出决策，则$l_i=\#$。因此，如果$L$是一个部分政策，它可以通过分支扩展为多个完整政策，这些政策由集合$D(L)$表示。在B&B树的根节点上，尚未对任何客户做出激励决策（对所有$i\in N，l_i=\#$）。分支操作在激励决策上进行。每次对节点$L$进行分支决策时，都会选择一个尚未做出激励决策的客户$i\in N$（即$l_i=\#$），并创建两个新分支：一个分支中客户$i$获得激励，另一个分支中客户$i$不获得激励。在对节点$L$进行分支后，获得两个新的子节点$L_0$和$L_1$，其中$l_i^0=0,l_i^1=1$, 且对所有$j\ne i，l_j^0=l_j^1=l_j$。B&B算法递归地继续执行，直到没有剩余的节点可以进行分支。本文B&B算法依赖于两种不同的技术来修剪搜索树的部分内容：(1)支配规则和 (2)履行成本的界限。

3.1 Dominance Rules

在本文的B&B树中，Dominance Rules建立在共享相同父节点 $L$ 的一对节点 $L_0$ 和 $L_1$ 之间。在 $L_1$ 中，该客户获得了激励；而在 $L_0$ 中，该客户没有获得激励。作者基于以下的标准建立Dominance Rules：即如果零售商向客户提供激励，那么零售商所承担的激励成本必须导致预期路由成本的降低，且这种降低程度必须高于激励本身的成本。用数学语言表述为：

Dominance Rules 1

a) 如果${\max }_{y\in D(L)}{\overline{F}}_k(y)\le d_k$,则点$L^1$被点$L^0$支配，$L^1$可以在B&B树中被剪掉。
b) 如果${\min }_{y\in D(L)}{\underline{F}}_k(y)\ge d_k$,则点$L^0$被点$L^1$支配，$L^0$可以在B&B树中被剪掉
在上述不等式中，左侧表示提供激励后减少的路由成本，不等式右侧表示提供激励本身的成本。

Dominance Rules 2

设两个客户$j,k\in N$ 位于距离$c_{jk}\le \frac{1}{2}\min (d_j,d_k)$之内，那么任何只为这两个客户中恰好一个提供激励的节点，都被为这两个客户都不提供激励的节点所支配。

3.2 履行成本的边界

履行成本由两个部分组成：预期激励成本和预期路由成本。
$$LB(L)=\underline{I}(L)+\underline{R}(L)=\sum _{\begin{array}{c}i\in N\\ l_i=1\end{array}}{d}_i{\Delta }_i+\underline{R}(L)(14)$$
U B ( L ) = I ‾ ( L ) + R ‾ ( L ) = ∑ i ∈ N l i ∈ { 1 , # } d i Δ i + R ‾ ( L ) ( 15 ) UB(L) = \overline{I}(L)+\overline{R}(L) = \sum_{\substack{i \in N\\l_i \in \{ 1,\#\}}}d_i\Delta_i +\overline{R}(L) \quad (15) UB(L)=I(L)+R(L)=i∈Nli​∈{1,#}​∑​di​Δi​+R(L)(15)
最低预期激励成本$\underline{I}(L)$是通过除了节点$L$中已经做出的决策外，不提供任何额外的激励的策略实现。类似地，最大预期激励成本$\overline{I}(L)$是通过除了节点$L$中已经指示的决策外，还提供最大可能数量的激励来实现的。与激励成本的界限类似，我们可以推导出预期路由成本的上界$\overline{R}(L)$和下界$\underline{R}(L)$。

预期路由成本的下界

$$\underline{R}(L)=\underset{\begin{array}{c}y\in D(L)\end{array}}{\min }\sum _{\omega \in \Omega }{P}_{\omega }(y)C_{\omega }(16)$$
在实际应用中，即使对于小规模的问题实例，这个表达式也难以处理，因为集合$\Omega$和$D(L)$可能非常大。作者提出了以下场景捆绑过程来解决此问题：首先，$\Omega$被划分为不重叠的子集，称为捆绑（bundles）。场景的划分基于在每个场景中需要经过的自提点子集$\tilde{\mathcal{P}}\subseteq \mathcal{P}$，捆绑$B(\tilde{\mathcal{P}})$包含了以下场景为：$\tilde{\mathcal{P}}$中包含的所有自提点都被访问，没包含的自提点都不访问。$\omega (\tilde{\mathcal{P}})$表示捆绑$B(\tilde{\mathcal{P}})$具有最低路由成本的场景，即所有客户都选择了离自己最近的自提点。然后，对于捆绑中的所有场景，计算一个单一的路由成本下界。接着，通过对每个捆绑的下界乘以从$L$得出的每个捆绑中场景的最小可能累积概率，并将这些乘积相加，即可获得预期路由成本的有效下界。当确定有客户选择上门配送时，下界就会变得更紧。因此，如果用$W\subseteq \Omega$表示路由成本$C_{\omega }$能被精准计算的场景子集时有：
$$\underline{R}(L)\le \sum _{\omega \in W}(C_{\omega }\underset{\begin{array}{c}y\in D(L)\end{array}}{\min }{P}_{\omega }(y))+\sum _{\tilde{\mathcal{P}}\subseteq \mathcal{P}}(C_{\omega }(\tilde{\mathcal{P}})\sum _{\begin{array}{c}\omega \in B(\tilde{\mathcal{P}})\\ \omega \notin W\end{array}}\underset{\begin{array}{c}y\in D(L)\end{array}}{\min }{P}_{\omega }(y))(18)$$

预期路由成本的上界

设 $\overline{C}$ 为车辆访问集合 $V$ 中所有顶点的某一场景的成本。通过设定 $\overline{R}(L)=\overline{C}$，可以获得路由成本 $\overline{R}(L)$ 的一个上界。类似于下界的计算，使用集合 $W\subseteq \Omega$ 作为已经准确计算路由成本的场景集，利用场景$\omega \in W$的路由成本 $C_{\omega }$，可以得到预期路由成本$\overline{R}(L)$的更紧上界：
$$\overline{R}(L)\equiv \sum _{\omega \in W}{C}_{\omega }\underset{y\in D(L)}{\min }{P}_{\omega }(y)+\overline{C}\left(1-\sum _{\omega \in W}\underset{y\in D(L)}{\min }{P}_{\omega }(y)\right)(19)$$

3.3 Branch-and-Bound 算法介绍

如Algorithm 1所示，B&B 算法从一个未探索的树节点的队列$L$开始，该队列以搜索树的根节点初始化，该节点表示一种未对任何顾客做出激励决策的部分策略。除此之外作者还计算了集合$W$ 中场景的确切路由成本，从而帮助初始化场景捆绑过程，以计算节点 $L$ 的预期履行成本的下限，即 $LB(L)$。最后，不对任何顾客提供激励的策略作为初始解$y^{\ast }$。

在 B&B 算法的每次迭代中，总是从队列中取出下界$LB(L)$ 最小的节点。在从队列中移除节点$L$ 后，检查是否有其他节点支配节点 $L$。如果节点$L$ 被支配，则该节点将被丢弃（第 1 行）。否则，使用公式（14）和（15）计算节点 $L$ 的下界和上界 $LB(L)$ 和 $UB(L)$（第 1 行）。然后将节点 LLL 与现有解 $y^{\ast }$ 进行比较。此比较可能产生三种结果：

(i). 下界$LB(L)$ 超过现有解的上界 $UB(y^{\ast })$，剪掉。

(ii). 如果 $UB(L)<LB(y^{\ast })$，则$D(L)$中的每个解都优于现有解。如果$D(L)$ 是单例，则找到了一个新的改进解，该解成为新的现有解（第 1 行）。

(iii). 如果$L$ 和$y^{\ast }$的界限重叠，则这两个节点不可比较。此情况的处理取决于$L$是树节点还是叶节点。

如果节点$L$是叶节点，并且其界限与现有解的界限重叠，那么无法确定哪一个节点构成更优解。为了解决这个问题，需要不断细化两个节点的界限，直到可以决定哪一个节点更优，然后相应地更新现有解。

当节点$L$是树节点且其界限与现有解的界限重叠时，改善节点$y^{\ast }$的界限，直到其下界和上界之间的差距小于节点$L$的下界和上界之间的差距（第 22 行），然后继续对$L$进行分支。

如果树节点无法基于支配或界限被丢弃，则需要进行分支（第 26 行）。当算法在节点$L$上进行分支时，选择一个尚未做出激励决策的顾客$i\in N$。当有多个这样的顾客时，我们选择与最近取件点$t\in P$和仓库的距离之和最大的顾客，因为服务这样的顾客可能对路由和激励成本产生最大的影响。此选择规则旨在对目标函数产生显著变化。对于不向顾客$i$提供激励的分支节点，可以确定顾客$i$将在家中被访问。因此，作者更新包含最近取件点的捆绑包的路由成本下限，以便该取件点距离顾客 iii 最近。在这样的捆绑包中，场景$\omega (\tilde{\mathcal{P}})$ 将被更新为顾客$i$需要在家访问而不是取件点交付的场景（其他元素保持不变）。分支后可得到两个新的子节点 $L_0$和$L_1$，将它们添加到开放节点的队列$L$中（第 30 行）。当队列中没有剩余可探索的开放节点时，B&B 算法终止（第 1 行）。

3.4 启发式实例

通过抽样估计期望路由成本

为了精确评估在B&B树的叶节点获得的完整策略$y$的期望路由成本，作者应用蒙特卡洛抽样。在这种方法中，我们反复生成一个随机场景$\omega$，其中对于每个客户$i\in N$，${\omega }_i$ 组件是一个由概率 $P_{{\omega }_i}(y_i)$决定的随机二元值。获得$M$个随机场景${\omega }^1,\dots ,{\omega }^M$ 后，计算路由成本的算术平均值，即 $\frac{1}{M}{\sum }_{j=1}^M{C}_{{\omega }^j}$，并将其作为策略y的期望路由成本的估计值。

提供激励的数量限制

作者添加了一条启发式剪枝规则，如果某个节点提供的激励超过预定义的限制，则对其进行剪枝。

4. 数值实验

首先，作者从可用客户中随机选择不超过50个客户，生成两组实例：A组包含100个小实例（n取值10, 11, …, 19，每个规模n有10个实例），B组包含70个大实例（n取值20, 25, …, 50，每个规模n有10个实例）。接着，我们随机选择一个仓库。并识别每个客户最近的自提点，并随机选择其中五个纳入模型。我们实验不同的取货点数量$p$为1, 3, 5。假设所有客户$i$的激励有效性$\Delta$为相同。将 $\Delta$ 设置为0.3，0.6和0.9。为了实现相同的激励有效性 $\Delta$，现实情况是，零售商需要向距离取货点较远的客户支付更高的激励，而不是向较近的客户支付的激励。为反映这种关系，激励值 $d_i$（对于每个$i\in N$）被设定为 $d_i=\frac{c_{i}u{C}_{\omega }}{n}$，其中 $c_i$是客户$i$到最近取货点的距离，$C_{\omega }$是当所有客户在家中服务时产生的路由成本，$u$是缩放因子。在实验中，作者评估了 $u$ 为0.03、0.06和0.12的情况。当 $u=0.06$ 时，最大激励成本（即，如果所有客户都获得激励且都接受激励）大约是最大路由成本的三分之一（即，如果所有客户请求家庭配送）。

为了结构化计算评估，评估创建了以下五个参数组合：

1. C1 基准案例: Δ=0.6， u=0.06。
2. C2 低激励有效性: Δ=0.3， u=0.06。
3. C3 高激励有效性: Δ=0.9， u=0.06。
4. C4 低激励值: Δ=0.6， u=0.03。
5. C5 高激励值: Δ=0.6， u=0.12。

• 枚举方法与B&B方法性能比较：枚举法不适合解决更大的实例。所有 $n\ge 18$的实例都需要超过两小时，而$n\ge 19$的实例因内存限制无法解决。B&B算法的性能显著优于枚举方法。例如，对于$n\ge 18$的实例，B&B算法的平均速度是枚举的6.1倍，某些实例几乎瞬间解决。
• 时间分配比较：枚举方法平均将20%的运行时间用于解决场景子问题，其余时间用于枚举和计算所有可用策略的期望履行成本。相对而言，B&B方法将大部分运行时间（77%）用于场景子问题。算法的其他部分，包括场景捆绑以计算期望路由成本的下界，收紧期望路由成本的上下界和，以及分支时间，分别占据平均2%、14%和7%的运行时间。主导性检查几乎是瞬时的。
• Dominance Rules 对时间性能的优化：对于大规模问题，当完全移除主导性规则时，解决时间增加了六倍以上（例如， $n=18$）。这是因为被主导性规则剪去的节点通常位于树的较高位置，而通过界定剪去的节点大多是叶节点。由于主导性规则防止了探索更多节点的高成本程序，且执行几乎是瞬时的，因此尽管剪去的节点较少，它们仍显著减少了解决时间。为了评估哪种主导性规则在解决时间上带来最大收益，评估结果显示，DR2是最强的（例如，比仅实施DR1和界定的情况快两倍）。
• 证明最优性的时间远大于找到最优解的时间：正如许多B&B算法的典型情况，高质量解决方案在搜索的早期阶段就被发现，大部分计算时间则用于证明最优性。例如，即使对于$n=16$的实例，平均而言，在53.3秒内达到最优解决方案，但证明最优性需要162.9秒。对于最大的实例（$n=19$），在一小时内，50个实例中有32个被解决并证明为最优；其余实例的最优性间隙平均为0.05%。这表明，即使对于更大的实例，该算法也能够在合理的计算时间内找到接近最优的解决方案。
• 启发式变体算法性能：

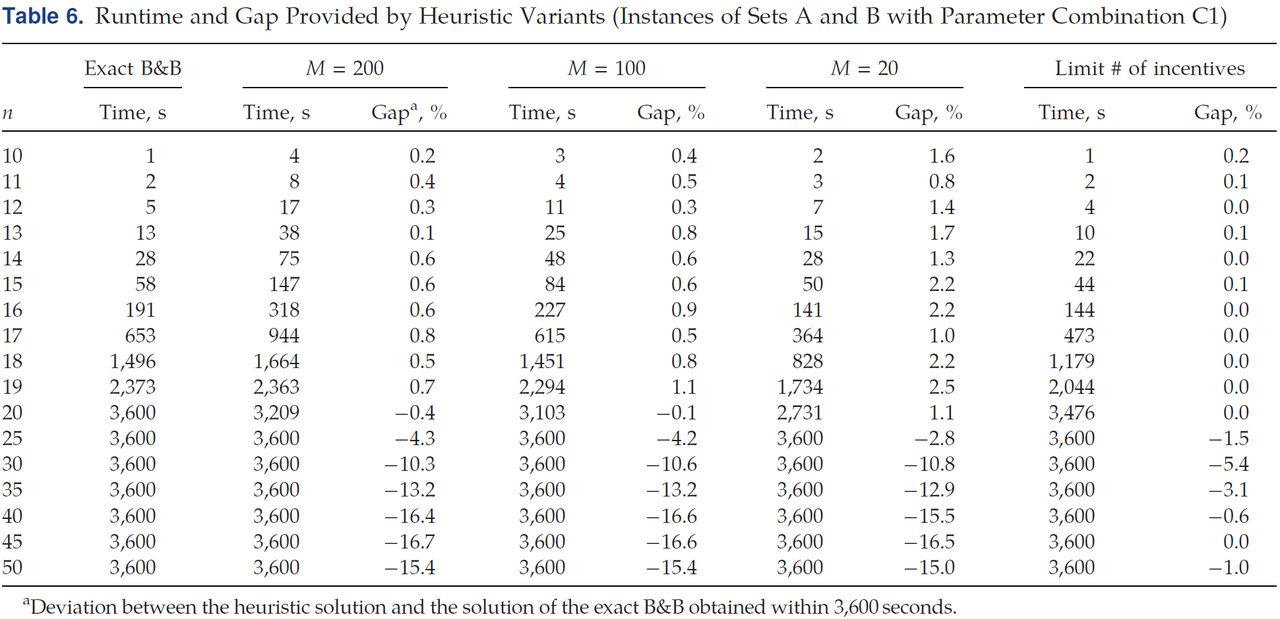
计算在实例集A和B上进行，使用参数组合C1（基准案例）。作者测试了三种不同的样本大小 $M=20,100,200$。Table 6展示了平均运行时间在启发式解决方案与精确B&B算法解决方案之间的差距。表6中，当精确B&B算法在给定时间内无法找到最优解时，启发式算法可以在相同计算时间内提供更好的解决方案。

Table 6显示，随着样本大小$M$的增加，算法的运行时间也增加；然而，启发式解与精确方法提供的解决方案之间的差距如预期变小。由于所有问题规模小于等于17的实例可以在3600秒内解决为最优，"gap"列表示这些问题规模的最优性间隙。可以观察到，使用 $M=200$ 和 $M=100$ 的启发式方法时，最优性间隙小于0.9%，而且节省的时间相当可观。即使在样本大小为$M=20$的情况下，对于包含15至17个客户的实例，计算时间减少约30%，而解决方案质量仅下降2.2%。对于规模在30到50的大问题，样本大小对解决方案质量的影响不大，因为这些问题需要评估的场景较多，探索的样本大小会有限。然而，整体而言，启发式B&B变体在相同时间内提供的解决方案质量优于精确B&B算法。例如，对于规模为30到50的问题，使用 $M=200$的采样启发式的B&B算法提供的解决方案比精确算法的结果好多达16.7%。

作者还测试了另一种启发式变体，Table 6中的“Limit # of incentives”列报告了启发式解决方案与精确B&B算法在一小时内获得的解决方案之间的平均运行时间和差距。对于规模小于等于20的问题，这种启发式方法最多减少18%的运行时间，而解决方案质量几乎没有下降。对于更大的问题规模，启发式解决方案好达5.4%，而解决时间与精确算法相似。

5. 总结与展望

这篇研究引入了一种新的最后一公里配送问题，其中零售商通过激励客户选择自提点配送，以最小化成本。客户可以选择接受或拒绝激励，这导致基于随机决策的结果，使得该问题在计算上极为困难。为了解决这一问题，作者开发了一个精确的分支定界（B&B）算法，能够最优地解决最多包含19位客户的实例。我们还在B&B框架内提出了启发式变体，用于为最多包含50位客户的实例找到近似最优解。未来此方向一个自然的扩展是考虑具有多辆有限容量车辆和自提点的情景。另一个研究方向是考虑客户请求具有随机性且其位置事先未知的情境。最后，所提出的需求引导机制基于对客户选择行为和激励效果的假设，建议未来研究方向可以进一步深入了解客户行为，并在最后一公里配送背景下探索更为先进的离散选择模型。

参考文献：

[1] Albina Galiullina, Nevin Mutlu, Joris Kinable, Tom Van Woensela (2024) Demand Steering in a Last-Mile Delivery Problem with Home and Pickup Point Delivery Options. Transportation Science 58(2):454-473.

[2] Labbé M, Laporte G, Martín IR, González JJS (2004) The ring star problem: Polyhedral analysis and exact algorithm. Networks 43(3):177–189.