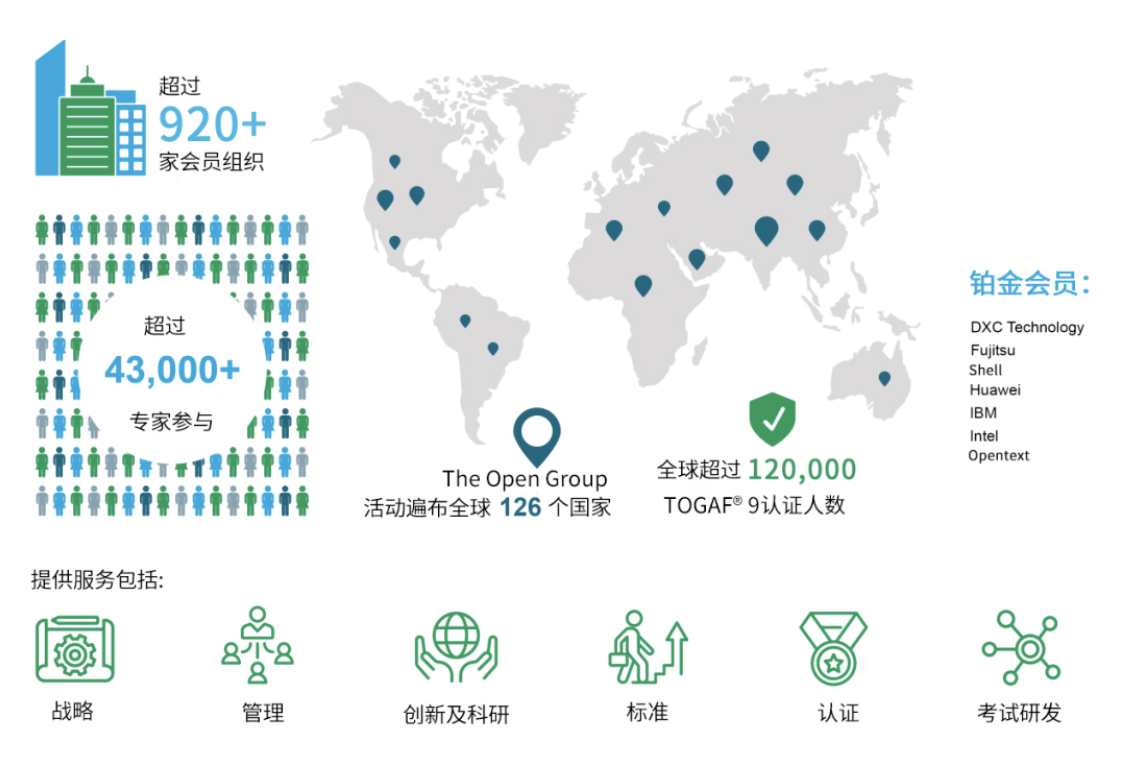
用途:研究多个自变量(也称为预测变量或解释变量)与一个因变量(也称为响应变量)之间的线性关系。
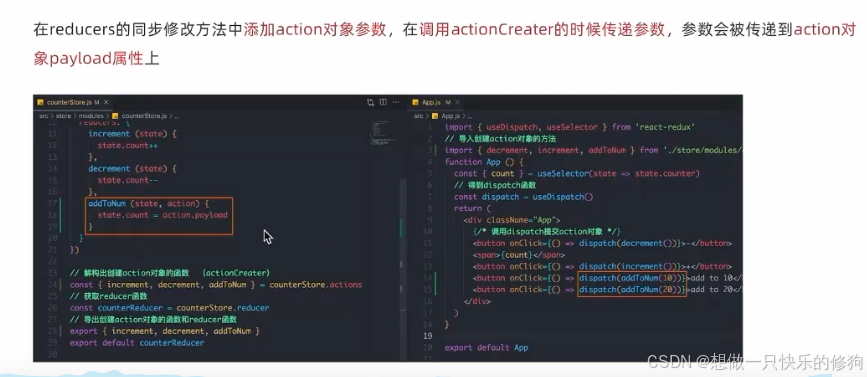
多元线性回归分析模型:Y=β0+β1X1+β2X2+…+βkXk+ϵ
- Y 是因变量。
- 1,X2,…,Xk 是自变量。
- β0 是截距项。
- β1,β2,…,βk 是各自变量的系数,表示每个自变量变化一个单位时因变量YY的平均变化量。
- ϵ 是误差项。
案例:收入与电视广告费、报纸广告费分析
方法:利用【数据分析】工具进行回归分析
1)点击【数据>数据分析】,选择【回归】后点确定。
![[图片]](https://i-blog.csdnimg.cn/direct/10d51e98b60d478da3bd97842f9db339.png)
2)设置输入、输出,勾选线性拟合图,点击确认。
![[图片]](https://i-blog.csdnimg.cn/direct/0582bb1a25ca42af9cb5df16aa267e4c.png)
得到以下结果:
![[图片]](https://i-blog.csdnimg.cn/direct/be92b3acc0ad4362b18db4c1e6cd1b02.png)
3)数据解析
- 回归统计:
- Multiple R:0.96396,这是相关系数,表示自变量和因变量之间的线性关系的强度。接近1的值表示非常强的正相关。
- R Square:0.92921,这是决定系数,表示因变量的变异中有多少是由自变量解释的。接近1的值表示模型解释了大部分的变异。
- Adjusted R Square:0.9009,这是调整后的决定系数,考虑了模型中自变量的数量。它提供了一个更准确的模型拟合度量。
- 标准误差:0.60085,这是实际观测值与回归线预测值之间差异的标准差。较小的标准误差表示模型的预测更准确。
- 观测值:8,这是用于回归分析的数据点的数量。
- 方差分析(ANOVA):
- 回归分析:
- df(自由度):2
- SS(平方和):23.6949
- MS(均方):11.8474
- F(F统计量):32.8163
- P-value(P值):0.0013333,这是一个非常小的值,表示模型在统计上是显著的,自变量对因变量有显著影响。
- 残差:
- df(自由度):5
- SS(平方和):1.80512
- MS(均方):0.36102
- 总计:
- df(自由度):7
- SS(平方和):25.5
- 系数:
- Intercept(截距):83.2828,这是当所有自变量为0时因变量的预测值。
- 电视广告费用/千元:2.28384,这是电视广告费用每增加1千元时,因变量(每周收入)的预测增加量。
- 报纸广告费用/千元:1.27496,这是报纸广告费用每增加1千元时,因变量(每周收入)的预测增加量。
- 标准误差:分别为截距、电视广告费用和报纸广告费用的标准误差。
- t Stat(t统计量):分别为截距、电视广告费用和报纸广告费用的t统计量。
- P-value(P值):分别为截距、电视广告费用和报纸广告费用的P值。电视广告费用的P值非常小,表示在统计上是显著的;报纸广告费用的P值0.00689也表明在统计上是显著的。
- Lower 95% 和 Upper 95%:这些是截距、电视广告费用和报纸广告费用的95%置信区间。
- 残差分析:
- 表格列出了每个观测值的每周收入、残差、标准残差。残差是实际观测值与回归线预测值之间的差异。标准残差是残差除以标准误差。
- 残差的正负和大小可以提供模型拟合度的信息。
- 残差图:
- 提供了两个残差图,一个针对电视广告费用,另一个针对报纸广告费用。这些图可以帮助识别残差的模式,检查模型的假设,如误差项的独立性和常数方差。
总结来说,这些数据表明电视广告费用和报纸广告费用与每周收入之间存在显著的正线性关系,回归模型非常显著,并且可以很好地预测每周收入。残差分析和残差图可以进一步帮助诊断模型的假设是否得到满足。
4)总结
对应回归方程为:Y=83.28+2.28X1+1.27X2。
方程总体拟合优度为0.900,且通过了F检验,因此回归方程总体显著;从回归系数的检验来看,两个自变量对应的回归系数的p值均小于0.05,因此,两个自变量均对总收入有显著影响。