【算法篇】二叉树类（2）（笔记）

一、Leetcode 题目

1. 左叶子之和

（1）迭代法

（2）递归法

2. 找树左下角的值

（1）广度优先算法

（2）递归法

3. 路径总和

（1）递归法

（2）迭代法

4. 从中序与后序遍历序列构造二叉树

5. 从前序与中序遍历序列构造二叉树

6. 最大二叉树

7. 合并二叉树

（1）递归法

（2）迭代法

8. 二叉搜索树中的搜索

（1）递归法

（2）迭代法

9. 验证二叉搜索树

（1）递归法

（2）迭代法

10. 二叉搜索树的最小绝对差

11. 二叉搜索树中的众数

（1）递归法

（2）迭代法

一、Leetcode 题目

1. 左叶子之和

404. 左叶子之和 - 力扣（LeetCode）https://leetcode.cn/problems/sum-of-left-leaves/description/

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:
输入: root = [1]
输出: 0

思路：

判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

（1）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return 0;
        st.push(root);
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
                result += node->left->val;
            }
            if (node->right) st.push(node->right);
            if (node->left) st.push(node->left);
        }
        return result;
    }
};

（2）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        // 递归法
        if (root == nullptr) return 0;
        if (!root->left && !root->right) return 0;

        int leftNum = sumOfLeftLeaves(root->left);
        if (root->left && !root->left->left && !root->left->right) {
            leftNum += root->left->val;
        }
        int rightNum = sumOfLeftLeaves(root->right);
        
        return leftNum + rightNum;
    }
};

2. 找树左下角的值

513. 找树左下角的值 - 力扣（LeetCode）https://leetcode.cn/problems/find-bottom-left-tree-value/submissions/567011451/

给定一个二叉树的根节点 root，请找出该二叉树的最底层最左边节点的值。假设二叉树中至少有一个节点。

示例 1:
输入: root = [2,1,3]
输出: 1

示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7

（1）广度优先算法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        // 层序遍历
        queue<TreeNode*> record;
        int result = 0;
        if (root != nullptr) {
            record.push(root);
            result = root->val;
        }
        while (!record.empty()) {
            int size = record.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = record.front(); record.pop();
                if (i == 0) result = node->val;
                if (node->left) record.push(node->left);
                if (node->right) record.push(node->right);
            }
        }
        return result;
    }
};

（2）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int result;
    int maxdepth = INT_MIN;
    void traversal(TreeNode* node, int depth) {
        if (node == nullptr) return;
        if (!node->left && !node->right && depth > maxdepth) {
            maxdepth = depth;
            result = node->val;
            return;
        }
        traversal(node->left, depth + 1);
        traversal(node->right, depth + 1);
    }

    int findBottomLeftValue(TreeNode* root) {
        traversal(root, 0);
        return result;
    }
};

3. 路径总和

112. 路径总和 - 力扣（LeetCode）https://leetcode.cn/problems/path-sum/description/

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

示例 1：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

思路：

递归：可以用递减，让计数器 count 初始为目标和，然后每次减去遍历路径节点上的数值。如果最后 count == 0，同时到了叶子节点的话，说明找到了目标和。如果遍历到了叶子节点，count 不为 0，就是没找到。（代码中包含着回溯）

迭代：栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。c++就用pair结构来存放这个栈里的元素。

定义为：pair<TreeNode*, int> pair<节点指针，路径数值> 这个为栈里的一个元素。

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool PathSum(TreeNode* node, int targetSum) {
        if (node == nullptr) return false;
        if (!node->left && !node->right && targetSum == node->val) return true;

        bool leftTree = PathSum(node->left, targetSum - node->val);
        bool rightTree = PathSum(node->right, targetSum - node->val);
        
        return leftTree || rightTree;
    }

    bool hasPathSum(TreeNode* root, int targetSum) {
        if (root == nullptr) return false;
        return PathSum(root, targetSum);
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        // 遍历法
        stack<pair<TreeNode*, int>> record;
        if (root == nullptr) return false;
        record.push(pair<TreeNode*, int>(root, root->val));
        while (!record.empty()) {
            pair<TreeNode*, int> node = record.top();
            record.pop();
            if (!node.first->left && !node.first->right && node.second == targetSum) return true;
            if (node.first->right) {
                record.push(pair<TreeNode*, int>(node.first->right
                            ,node.second + node.first->right->val));
            }
            if (node.first->left) {
                record.push(pair<TreeNode*, int>(node.first->left
                            ,node.second + node.first->left->val));
            }
        }
        return false;
    }
};

4. 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例 1:
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:
输入：inorder = [-1], postorder = [-1]
输出：[-1]

思路：

递归：

第一步：如果数组大小为零的话，说明是空节点了。

第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）

第五步：切割后序数组，切成后序左数组和后序右数组

第六步：递归处理左区间和右区间

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* bTree(vector<int>& inorder, int inorderbegin, int inorderend
                   ,vector<int>& postorder, int postorderbegin, int postorderend) {
        
        if (postorderbegin == postorderend) return nullptr;

        // 获取根元素
        int mid = postorder[postorderend - 1];
        TreeNode* root = new TreeNode(mid);

        if (postorderend - postorderbegin == 1) return root;

        // 找到中序遍历中的根元素
        int inorderIndex;
        for (inorderIndex = inorderbegin; inorderIndex < inorderend; inorderIndex++) {
            if (mid == inorder[inorderIndex]) break;
        }

        // 中序遍历更新索引 [)
        int inorderbeginleft = inorderbegin;
        int inorderendleft = inorderIndex;

        int inorderbeginright = inorderIndex + 1;
        int inorderendright = inorderend;

        // 后序遍历更新索引 [)
        int postorderbeginleft = postorderbegin;
        int postorderendleft = postorderbeginleft + (inorderIndex - inorderbegin);

        int postorderbeginright = postorderendleft;
        int postorderendright = postorderend - 1;
        
        // for (int i = inorderbeginleft; i < inorderendleft; i++) {
        //     cout << inorder[i] << " ";
        // }
        // cout << endl;
        // for (int i = inorderbeginright; i < inorderendright; i++) {
        //     cout << inorder[i] << " ";
        // }
        // cout << endl;

        // for (int i = postorderbeginleft; i < postorderendleft; i++) {
        //     cout << postorder[i] << " ";
        //     // cout << i << " ";
        // }
        // cout << endl;
        // for (int i = postorderbeginright; i < postorderendright; i++) {
        //     cout << postorder[i] << " ";
        //     // cout << i << " ";
        // }
        // cout << endl;


        root->left = bTree(inorder, inorderbeginleft, inorderendleft
                          ,postorder, postorderbeginleft, postorderendleft);

        root->right = bTree(inorder, inorderbeginright, inorderendright
                           ,postorder, postorderbeginright, postorderendright);

        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        if (!inorder.size() || !postorder.size()) return nullptr;
        return bTree(inorder, 0, inorder.size(), postorder, 0, postorder.size());
    }
};

5. 从前序与中序遍历序列构造二叉树

105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* bTree(vector<int>& preorder, int preorderbegin, int preorderend
                    ,vector<int>& inorder, int inorderbegin, int inorderend) {
        if (preorderbegin == preorderend) return nullptr;

        // 获取顶点节点
        int mid = preorder[preorderbegin];
        TreeNode* root = new TreeNode(mid);

        // 中序中遍历找到节点索引 [inorderbegin, inorderend)
        int inorderIndex;
        for (inorderIndex = inorderbegin; inorderIndex < inorderend; inorderIndex++) {
            if (mid == inorder[inorderIndex]) break;
        }

        // 更新前序遍历的索引 [preorderbegin, preorderend)
        int preorderbeginleft = preorderbegin + 1; 
        int preorderendleft = preorderbegin + (inorderIndex - inorderbegin) + 1;

        int preorderbeginright = preorderendleft;
        int preorderendright = preorderend;

        // 更新中序遍历的索引 [inorderbegin, inorderend)
        int inorderbeginleft = inorderbegin;
        int inorderendleft = inorderIndex;

        int inorderbeginright = inorderIndex + 1;
        int inorderendright = inorderend;

        // for (int i = preorderbeginleft; i < preorderendleft; i++) {
        //     cout << preorder[i] << " ";
        // }
        // cout << endl;
        // for (int i = preorderbeginright; i < preorderendright; i++) {
        //     cout << preorder[i] << " ";
        // }
        // cout << endl;

        // for (int i = inorderbeginleft; i < inorderendleft; i++) {
        //     cout << inorder[i] << " ";
        // }
        // cout << endl;
        // for (int i = inorderbeginright; i < inorderendright; i++) {
        //     cout << inorder[i] << " ";
        // }
        // cout << endl;

        root->left = bTree(preorder, preorderbeginleft, preorderendleft
                          ,inorder, inorderbeginleft, inorderendleft);

        root->right = bTree(preorder, preorderbeginright, preorderendright
                           ,inorder, inorderbeginright, inorderendright);

        return root;
    }


    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (!preorder.size() || !inorder.size()) return nullptr;
        return bTree(preorder, 0, preorder.size(), inorder, 0, inorder.size());
    }
};

6. 最大二叉树

654. 最大二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/maximum-binary-tree/description/

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的子数组前缀上构建左子树。
递归地在最大值右边的子数组后缀上构建右子树。

返回 nums 构建的最大二叉树。

示例 1：
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& nums, int beginIndex, int endIndex) {
        if (beginIndex == endIndex) return nullptr;

        // 获取中心元素
        int midIndex = beginIndex;
        for (int i = beginIndex; i < endIndex; i++) {
            midIndex = nums[i] > nums[midIndex] ? i : midIndex;
        }
        // cout << midIndex << endl;
        TreeNode* root = new TreeNode(nums[midIndex]);

        // 重定义左右节点
        int leftbeginIndex = beginIndex;
        int leftendIndex = midIndex;
        
        int rightbeginIndex = midIndex + 1;
        int rightendIndex = endIndex;

        // for (int i = leftbeginIndex; i < leftendIndex; i++) {
        //     cout << nums[i] << " ";
        // }
        // cout << endl;
        // for (int i = rightbeginIndex; i < rightendIndex; i++) {
        //     cout << nums[i] << " ";
        // }
        // cout << endl;


        root->left = buildTree(nums, leftbeginIndex, leftendIndex);
        root->right = buildTree(nums, rightbeginIndex, rightendIndex);

        return root;
    }

    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if (nums.size() == 0) return nullptr;
        return buildTree(nums, 0, nums.size());
    }
};

7. 合并二叉树

617. 合并二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/merge-two-binary-trees/description/

        给你两棵二叉树： root1 和 root2 。

        想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

        返回合并后的二叉树。

        注意: 合并过程必须从两个树的根节点开始。

示例 1：
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：
输入：root1 = [1], root2 = [1,2]
输出：[2,2]

思路：

递归：因为是传入了两个树，那么就有两个树遍历的节点root1 和 root2，如果root1 == NULL 了，两个树合并就应该是 root2 了（如果root2也为NULL也无所谓，合并之后就是NULL）。反过来如果root2 == NULL，那么两个数合并就是root1（如果root1也为NULL也无所谓，合并之后就是NULL）。

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        // 递归
        if (root1 == nullptr) return root2;
        if (root2 == nullptr) return root1;

        TreeNode* root = new TreeNode(0);
        root->val = root1->val + root2->val;
        root->left = mergeTrees(root1->left, root2->left);
        root->right = mergeTrees(root1->right, root2->right);
        
        return root;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
        if (t1 == NULL) return t2;
        if (t2 == NULL) return t1;
        queue<TreeNode*> que;   // 用于处理两棵树节点都有数的时候
        que.push(t1);
        que.push(t2);
        while(!que.empty()) {
            TreeNode* node1 = que.front(); que.pop();
            TreeNode* node2 = que.front(); que.pop();
            // 此时两个节点一定不为空，val相加
            node1->val += node2->val;

            // 如果两棵树左节点都不为空，加入队列
            if (node1->left != NULL && node2->left != NULL) {
                que.push(node1->left);
                que.push(node2->left);
            }
            // 如果两棵树右节点都不为空，加入队列
            if (node1->right != NULL && node2->right != NULL) {
                que.push(node1->right);
                que.push(node2->right);
            }

            // 当t1的左节点 为空 t2左节点不为空，就赋值过去
            if (node1->left == NULL && node2->left != NULL) {
                node1->left = node2->left;
            }
            // 当t1的右节点 为空 t2右节点不为空，就赋值过去
            if (node1->right == NULL && node2->right != NULL) {
                node1->right = node2->right;
            }
        }
        return t1;
    }
};

8. 二叉搜索树中的搜索

700. 二叉搜索树中的搜索 - 力扣（LeetCode）https://leetcode.cn/problems/search-in-a-binary-search-tree/description/

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:
输入：root = [4,2,7,1,3], val = 5
输出：[]

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        TreeNode* result = NULL;
        if (root->val > val) result = searchBST(root->left, val);
        if (root->val < val) result = searchBST(root->right, val);
        return result;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != nullptr) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return nullptr;
    }
};

9. 验证二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）https://leetcode.cn/problems/validate-binary-search-tree/description/

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：
输入：root = [2,1,3]
输出：true

示例 2：
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路：

① 陷阱 1：

不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了。我们要比较的是左子树所有节点小于中间节点，右子树所有节点大于中间节点。

② 陷阱 2：

样例中最小节点可能是int的最小值，如果这样使用最小的int来比较也是不行的。此时可以初始化比较元素为 longlong 的最小值。

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
// 方法一：讲所有的节点值保存到数组中，再进行比较
class Solution {
private:
    vector<int> vec;    // 保存到数组中再进行比较

    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }

public:
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 不加这句在leetcode上也可以过，但最好加上
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            // 小于等于，搜索树里不能有相同元素
            if (vec[i] <= vec[i - 1]) return false;
        }
        return true;
    }
};



// 方法二：记录递归的上个节点
class Solution {
public:
    TreeNode* pre = nullptr;    // 中序遍历，记录前一个节点，只要出现正在遍历的值小于上个节点的值，就返回 false
    bool isValidBST(TreeNode* root) {
        if (root == nullptr) return true;

        bool leftTree = isValidBST(root->left);
        if (pre && root->val <= pre->val) return false;
        else pre = root;
        bool rightTree = isValidBST(root->right);

        return leftTree && rightTree;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        TreeNode* cur = nullptr;
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                if (node->right) record.push(node->right);
                record.push(node);
                record.push(nullptr);
                if (node->left) record.push(node->left);
            }
            else {
                node = record.top();
                record.pop();
                if (cur && node->val <= cur->val) return false;
                cur = node; 
            }
        }
        return true;
    }
};

10. 二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）https://leetcode.cn/problems/minimum-absolute-difference-in-bst/description/

给你一个二叉搜索树的根节点 root ，返回树中任意两不同节点值之间的最小差值。差值是一个正数，其数值等于两值之差的绝对值。

示例 1：
输入：root = [4,2,6,1,3]
输出：1

示例 2：
输入：root = [1,0,48,null,null,12,49]
输出：1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 迭代法
class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        stack<TreeNode*> record;
        if (root != nullptr) record.push(root);
        TreeNode* cur = nullptr;
        int result = INT_MAX;
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                if (node->right) record.push(node->right);
                record.push(node);
                record.push(nullptr);
                if (node->left) record.push(node->left);
            }
            else {
                node = record.top();
                record.pop();
                if (cur) result = min(result, (node->val - cur->val));
                cur = node;
            }
        }
        return result;
    }
};

11. 二叉搜索树中的众数

501. 二叉搜索树中的众数 - 力扣（LeetCode）https://leetcode.cn/problems/find-mode-in-binary-search-tree/description/

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按任意顺序返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值小于等于当前节点的值
结点右子树中所含节点的值大于等于当前节点的值
左子树和右子树都是二叉搜索树

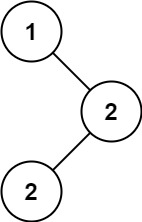
示例 1：
输入：root = [1,null,2,2]
输出：[2]

示例 2：
输入：root = [0]
输出：[0]

思路 1：

这个树都遍历了，用map统计频率。想直接对 map 中的 value 排序，还真做不到，C++中如果使用 std::map 或者 std::multimap 可以对 key 排序，但不能对value排序。所以要把map转化数组即 vector，再进行排序，当然vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。

数组 vector 中已经是存放着按照频率排好序的pair，那么把前面高频的元素取出来就可以了。

思路 2：

只需要遍历一次就可以找到所有的众数。频率count 大于 maxCount的时候，不仅要更新 maxCount（要把这个元素加入到结果集中），而且要清空结果集（以下代码为result数组），因为结果集之前的元素都失效了。

（1）递归法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 先统计后输出
class Solution {
public:
    void searchBST(unordered_map<int, int>& map, TreeNode* root) {
        if (root == nullptr) return;
        map[root->val]++;
        searchBST(map, root->left);
        searchBST(map, root->right);
        return;
    }

    bool static cmp(const pair<int, int> x, const pair<int, int> y) {
        return x.second > y.second;
    }

    vector<int> findMode(TreeNode* root) {
        // C++中如果使用std::map或者std::multimap可以对key排序，但不能对value排序
        // 设置大根堆
        unordered_map<int, int> map;
        vector<int> result;
        if (root == nullptr) return result;
        searchBST(map, root);

        // 放到 vector 中进行排序
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);
        result.push_back(vec[0].first);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[i - 1].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
};

（2）迭代法

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

// 方法一：（更新大根堆）
class Solution {
public:
    bool static cmp(const pair<int, int> x, const pair<int, int> y) {
        return x.second > y.second;
    }

    vector<int> findMode(TreeNode* root) {
        // 设置大根堆
        unordered_map<int, int> map;
        stack<TreeNode*> record;
        vector<int> result;
        if (root == nullptr) return result;
        record.push(root);
        while (!record.empty()) {
            TreeNode* node = record.top();
            record.pop();
            if (node != nullptr) {
                if (node->right) record.push(node->right);
                if (node->left) record.push(node->left);
                record.push(node);
                record.push(nullptr);
            }
            else {
                node = record.top();
                record.pop();
                map[node->val]++;
            }
        }
        // 放到 vector 中进行排序
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);
        result.push_back(vec[0].first);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[i - 1].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
};


// 方法二：（一次遍历）
class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = NULL;
        int maxCount = 0; // 最大频率
        int count = 0; // 统计频率
        vector<int> result;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top();
                st.pop();                       // 中
                if (pre == NULL) { // 第一个节点
                    count = 1;
                } else if (pre->val == cur->val) { // 与前一个节点数值相同
                    count++;
                } else { // 与前一个节点数值不同
                    count = 1;
                }
                if (count == maxCount) { // 如果和最大值相同，放进result中
                    result.push_back(cur->val);
                }

                if (count > maxCount) { // 如果计数大于最大值频率
                    maxCount = count;   // 更新最大频率
                    result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了
                    result.push_back(cur->val);
                }
                pre = cur;
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};