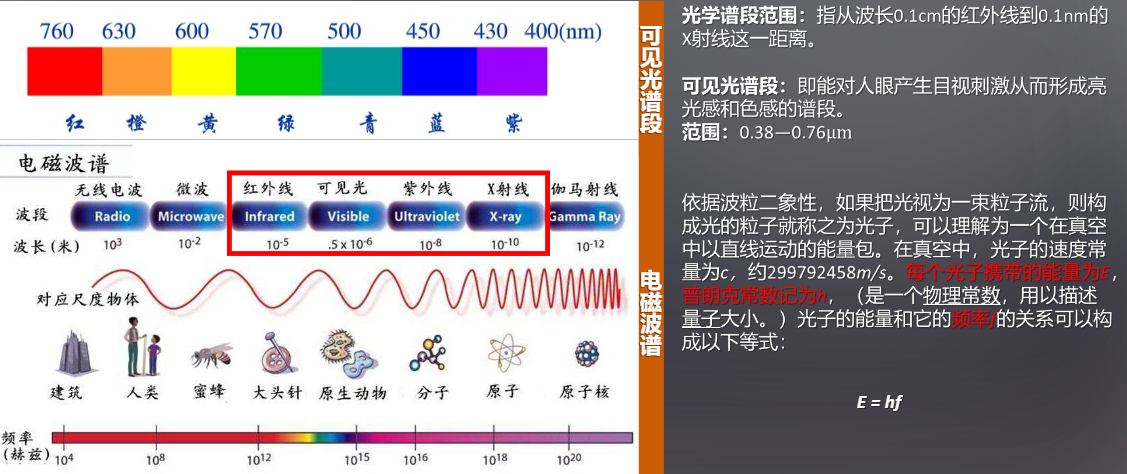
1. 辐射度学
定义:辐射度学是一门以整个电磁波段的电磁辐射能测量为研究的科学。
而计算机图形学中涉及的辐射度学,则集中于整个电磁波普中光学谱段中的可见光谱段的辐射能的计算。
1.1. 立体角
概念:单位球体上的一块区域对应的球面部分的面积。球面任意一块区域的面积等于球半径的平方,假设我们给定一个正球体,半径为R,再给定一个正圆锥体,正圆锥体的顶点与球心重合,到圆锥底面圆任意一点的连线,即正圆锥体的斜高(斜边),它的长度也为R。
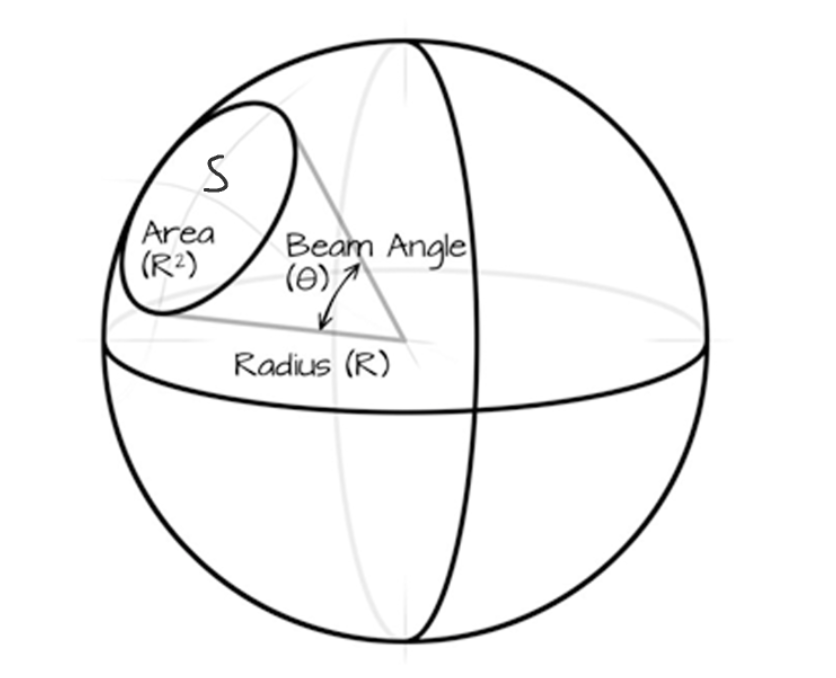
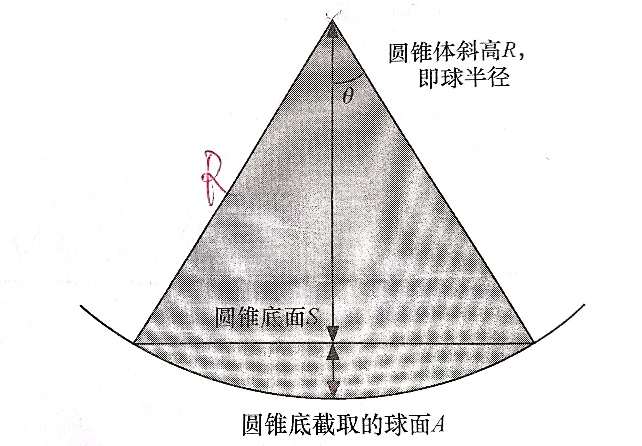
立体角截面
由正圆锥体的底面圆S所截取的那一部分球面的面积A和球体半径R的平方的比值称为立体角(球面度)。
单位立体角:一个立体弧度为半径1 米的球面上1 平方米面积所张的立体角。
如果以Ω表示立体角。立体角的微分形式,就是上图右边的公式的定义:
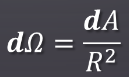
θ为光线与z轴的夹角,Φ为光线所在平面与y轴的夹角。假设黄色的矩形为单位立体角对应的面
- 小矩形竖边为rdθ
- 小矩形横边为rsinθdΦ
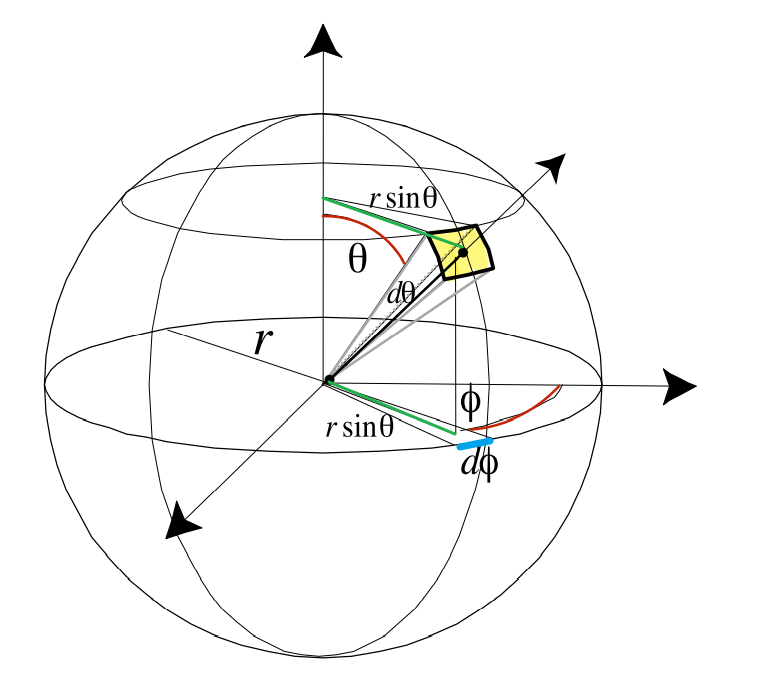
所以单位面积dA=长*宽
对于一整个球来讲(Φ为0到2pi,θ为0到pi)
如果在球面坐标系下对立体角进行定义,面积微元dA的公式可以写为以下这个等式:
![]()
然后由上式可以得出,整个球面的立体角可以写为θ和φ的一个二重积分式子,其中θ表示经度,φ表示维度,所以整个球面的立体角为4π,对于一个正方体的面而言,从该立方体的中心点测量的立体角为2/3π,整个球对应的立体角是整个球面的空间,就是又称为4π空间,同理半球所对应的立体角为2π空间。
1.2. 辐射通量 Radiation Flux
为了研究单位时间内,通过某表面的各个光子所携带的能量之和是多少,在物理学中引入了辐射通量这个概念,也就说在这段单位时间内,我得整个(通过表面)光的能量之和,辐射通量定义为以辐射的形式发射,传输或者接收的功率及单位时间内的一个辐射能,单位为W,记为φ。
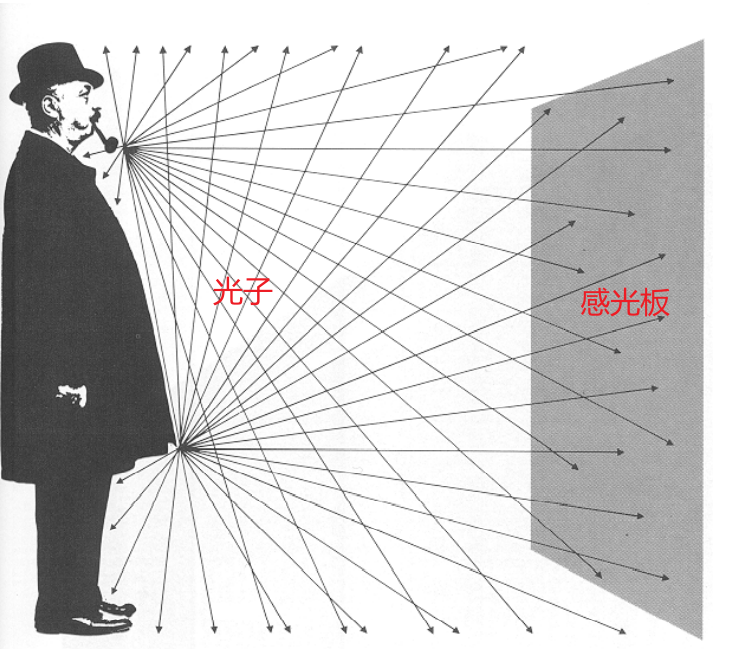
假设一个灯泡可以发出100瓦的辐射能量,都是基于这个辐射通量来测试能量,而不是使用总和的能量,所以这些度量都是在单位时间下发生的,不同的波长的光引入人对不同颜色的感知,然后不同的辐射通量则引起人对不同亮度的感知。
假设我们处于一个空间V,在这个空间内,光子虽然在物体表面不停地流过,但从总体上讲,光的分布保持一个常数。因为只要是一个恒定的光源,在被光所照亮的空间内的地方不会变的忽明忽暗。又因为光速过快,在开灯的一瞬间,对于观察者而言,光的能量几乎是传到空间的每一个角度,所以一起看起来都是一个恒定的常数。
在空间内,光子的流动与传播都遵循能量守恒的定律。所有流入空间内的光子的总能量,一定是等于从本空间流出的光子的能量之和。
该空间中,光有两种方式进入:
- 从外部空间流入(入射)的光,记为∅i
- 从本空间内部物体发射(反射)的光,记为∅e
光从空间内流出有三种方式:
- 不经过本空间任何干扰直接向外流出,记为∅s
- 被本空间内物体完全反射后流程(出射),记为∅o
- 被本空间内物体吸收,记为∅a.
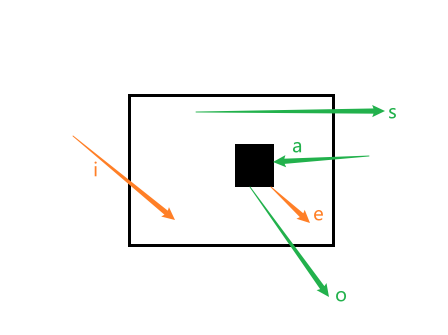
那么给定的单位时间内空间V的辐射通量的方程如下:

计算如下:
- 从本空间内部物体发射(反射)的光,记为∅e
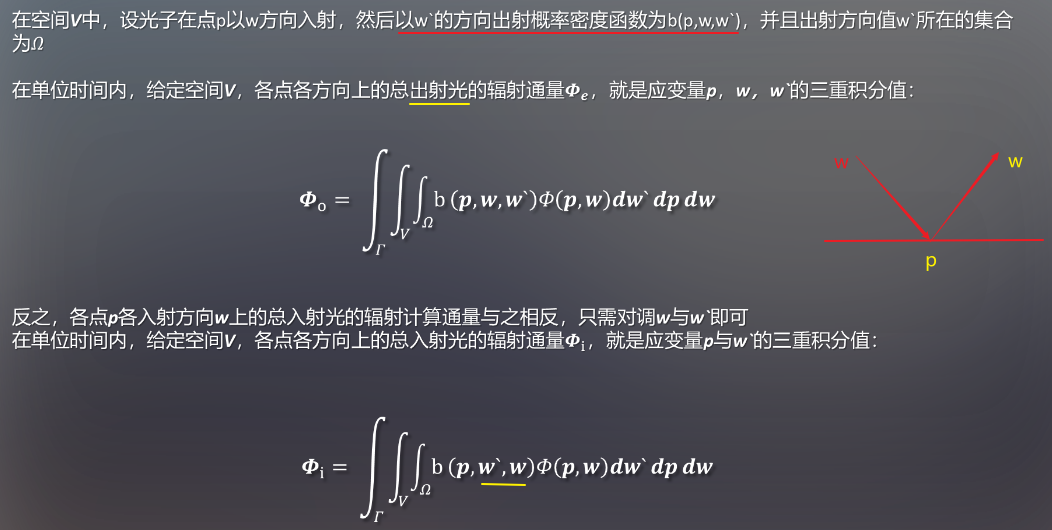
在空间V内,在某点P上有n多个方向,w是点P其中一个方向,在w方向上,由自发光发出的辐射通量为函数Σ(p,w)所得到的值。单位时间内,点p∈V,方向w∈Γ,p为v中的某一个的位置点,Γ为该点所有存在的入射与出射方向的集合,w为该集合中的一个值。
在单位时间内,给定空间V,各点和各方向的总自发光的辐射通量Φ,就是因变量的p和w的一个二重积分值。
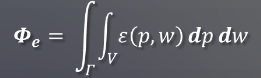
- 被本空间内物体吸收,记为∅a

- 被本空间内物体完全反射后流程(出射),记为∅o
- 从外部空间流入(入射)的光,记为∅i

- 不经过本空间任何干扰直接向外流出,记为∅s

1.3. 辐射强度 Radiation Intensity
辐射强度的定义是在给定的传输方向上,单位立体角内光源发出的辐射通量,辐射强度是指单位立体角内光源发出的一个辐射通量。辐射通量一般是作为Φ,立体角为Ω,辐射强度为I。
辐射强度可以以微分的形式做出如下定义:
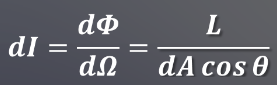
对于一个面A的区域求积分:
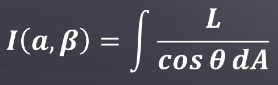
I称为表面面积微元dA在方向(α,β)上的辐射强度,它和距离无关。但是与发射面dA的面积有关,由于光通量通常具有一定的面积,所以说在图形学中常常使用I来表示一个光源的辐射强度分布。
上述公式的L是指辐射亮度。
1.4. 辐射亮度 Radiance
定义:辐射表面在其单位投影面积的单位立体角内发出的辐射通量。
什么是单位投影面积的单位立体角发出的辐射通量?

要进行两次微分,所以是
![]()
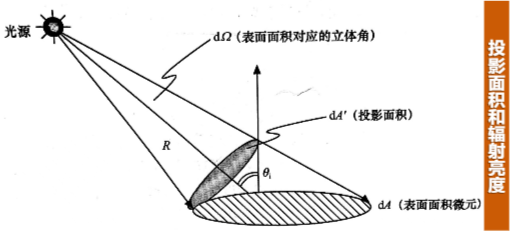
辐射亮度描述的是光源的表面面积微元在垂直传输方向上的辐射强度特性。好比单去描述一个白炽灯的某一块区域的发射特性是没有实际意义的,应该将它视作一个点光源整理,来描述在某个给定的观察方向上的辐射强度。
1.5. 辐射照度 Irradiance
辐射照度它是被用来测量光进入一个单位面积的强度,也可以表示光离开一个表面的强度,我们称之为入射度和出射度。
- 入射度的定义:单位面积内被照射的辐射通量。
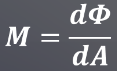
- 出射度的定义:离开光源表面的单位面积的一个辐射通量。
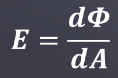
辐射的入射度和出射度,这个定义方程和单位都是相同的,这里为了区分,把M代表入射。 E代表出射。
它们分别用来描述面积微元发射和接受的辐射通量的特性,如果一个表面能完全反射全部的辐射通量,那么该表面可以视为一个辐射源表面,辐射度相关的物理量可以视为电磁波的波长函数。因此在描述辐射度相关的物理量时可以在相应的名称前面加上一个波长符号λ,写成函数的形式,例如辐射通量Φ可以记为Φ(λ)。辐射出射度和入射度的概念和基于物理渲染的模型有直接的关系。
对于点光源定义辐射通量为φ,则在一个半径为R的球面,某一面积微元的每一面积微元的入射度,遵循一个平方的反比定律。
平方反比定律是什么?
就是光源距离越近,然后亮度越大,它是为距离平方的一个倒数。

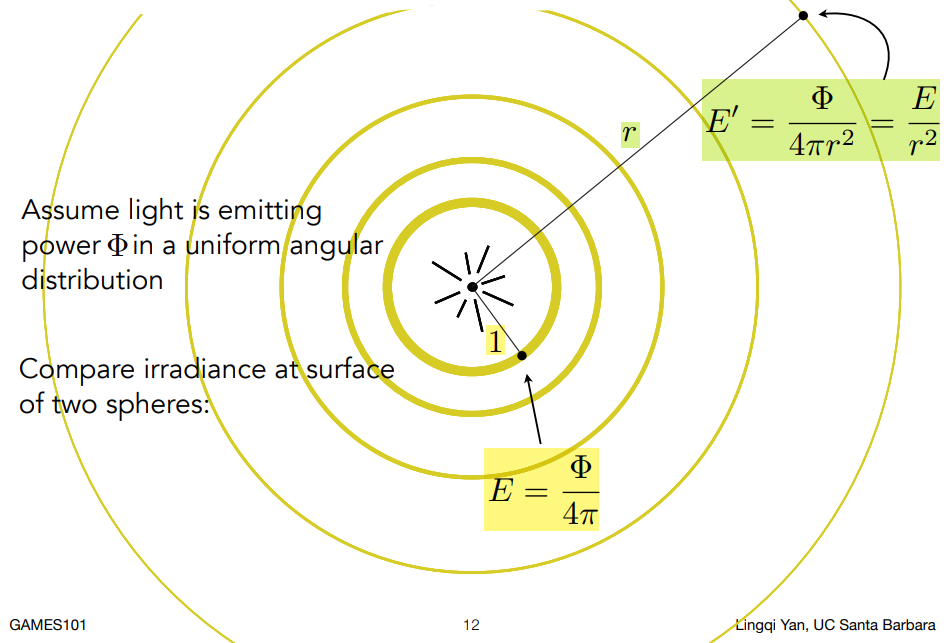
2. 光度学
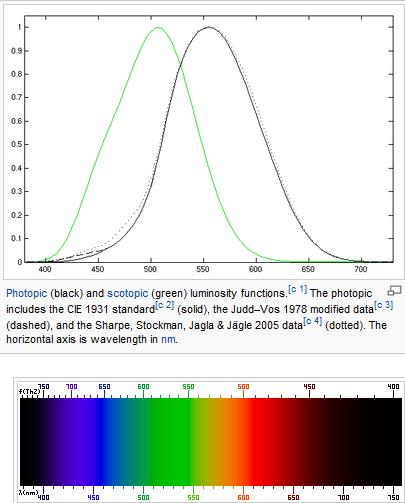
2.1. 视见函数
人眼的灵敏度用CIE光度拉姆达曲线是V(λ)表示,它遵循一条钟形的曲线,代表我们的眼睛对某些光波长的接收效率。下图是一个视见函数(链接辐射度量学和光度学的桥梁,是视见函数),人眼的灵敏度在555纳米处达到一个峰值,在我们看来是绿色。在这个波长上,灵敏度函数值为一个单位,意味着就是百分百的效率和辐射度。
2.2. 光度通量和辐射通量的转换
和辐射度量学相比,光度学的研究对象只限可见光的范围。并且要以人眼的视觉特性为基础。为了避免混淆,在辐射度量学的符号下标加上e,光度学符加上v。光度通量和辐射通量的转换公式:


光的度量和辐射量是有关系的,在可见光谱380-780纳米上面的整个积分,如下图公式所示:


2.3. Km
对于以上式子Km的定义:
1cd(坎德拉)指一个频率为540THz(波长为555nm)的单色辐射源在某一方向上的发光强度,在给定方向上的辐射强度为1/683 W/Sr,即Km=683。

- 光通量:1lm(1lm指光强度为1cd的均匀点光源在单位球面内发出的光通量)
- 发光强度:1cd
- 辐射强度:1/683 W/Sr
最早1cd(坎德拉)表示的是一根蜡烛的发光强度,即一根蜡烛在单位立体角内产生的光通量。但是蜡烛不是一个精确的定义方法,所以后来改为用单位波长的光强度来定义。而人也对于不同波长的敏感度是有区别的,在555nm时到达峰值,所以选用这个波长来定义。而1/683 W的555nm的单色光正好和一根蜡烛有相同的总光通量。
简单一句话表示就是1w绿光555nm的光是683lm。光度曲线还可以让我们推断出一盏光的光效,然后这个可以解释为一个光源产生了多少个可见光。
2.4. 发光效率η
下图是一个计算发光效率的公式:

上图公式中η的单位是lm/W。这个公式意味着绿光(555nm)的效能为683lm/w,这相当与100%的发光效率,不同类型的灯光的发光效率可能不同。也就是说,具有相同瓦数的两盏灯可以产生不同的感知强度。
在非光谱渲染的情况下,比如说游戏内,可以做一些简化,以便辐射通量和光通量单位之间的转换。提供一个灯的辐射功率和发光功率可以让我们将其功率从w(辐射通量)转换成lm(光通量)。
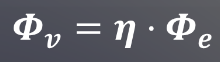
当没有这些信息时,我们通常会假设一盏灯的效率是100%,并以683来指代η(发光效率)。

对于非光谱渲染,就像大多数游戏引擎一样,光效信息是需要再辐射度和光度之间来回转换的,但是对于艺术家来说,提供两个值(光强和光效)会增加复杂性,所以最好使用假设η=683,在这样近似情况下,每个量都是另一个量的线性变换,因此它们的处理将是相同的,然后最好是能够在引擎中使用真实世界的光强,以便在感知上与现实世界中观察到的情况相匹配,100%光效的假设阻止了辐射参考值的使用,因为这将产生过亮的照明,好在商业照明提供了它们的光度特性。
3. 灯光类型
3.1. 精确光 Point Light
3.1.1. 反平方定律
Frostbite和Unity只支持两种类型的精确光:点光源和聚光灯。为了使精确光在物理上正确,它必须遵循反平方定律,从恒定亮度的光源观察到光强与物体距离的平方成正比下降。

平方反比定律只对点光源是有效的。它不适用于窄分布的泛光灯和探照灯,因为光束是高度聚光的区域灯,或者像菲涅尔透镜这样的特殊灯。
将平方反比定律转化为方程,可以得到光照度E=I/距离。

该方程要求在整个照明计算中,距离单位是均匀的(单位可以是米,厘米,毫米)。当距离趋向于0时,数值可以变得无穷大,但在现实生活中不会发生这种情况,一盏灯总会有一个大小。在图形中通常会添加一个小的偏差,也就是max函数,这样可以避免一个除以0的问题。
3.1.2. 点光源-球
在Frostbite和Unity中,1个单位=1米,定义精确光的尺寸为1cm,光通量Φ总是换算成发光强度I进行照面计算。通过对光强在光照立体角上的积分得到球的光照度:
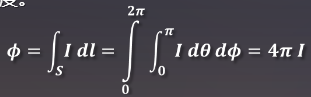
也就是Φ=4πl
3.1.3. 聚光灯-圆锥
以下公式是圆锥的精确立体角,如果θ_outer是半角,则积分变成:
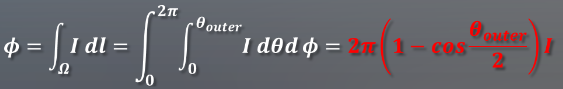
这是它是一个聚光灯,可以看到这个公式得到的一个结果是:对于相同的数值照明会更加集中,减小锥角的情况下照明会更亮。可以看到下图,随着发挥功率的增加,减小圆锥的半径会导致圆锥体内部照度的增加。

基于这些考虑,为了实现平滑过渡,将引擎中的聚光灯的光通量定义为:
Φ=πl
3.1.4. 小结
从光通量Φ到光强度I的转换,如下图所示:
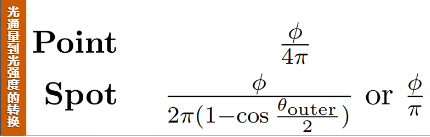
这些光源的光亮度L的计算结果如下,点光可以表示为以下这条公式:
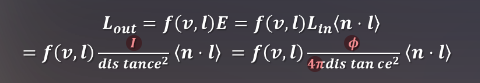
如果光直接指向表面的法线(n·l=1),那么得到的照度遵循平方反比定律的照度是

聚光灯可表示为:
![]()
由此得出的照度遵循平方反比定律,同样也考虑光直接指向表面的法线(n·l=1):

3.1.5. 窗口化
Attenuation(衰减):平方反比定律的一个问题是它永远不会达到0。比如说一个点光,它的光源永远都是不会衰减到0的。但是由于性能的原因,引擎必须实现在有限的光照范围内使得光照强度为0,以方便剔除灯光。灯光在边缘极限情况下,光照度应该是平滑地达到0。
解决这个问题的一种方法,是对falloff(衰减)进行窗口化的处理,使大部分功能不会受影响,它是使用基于距离的Lerp(插值)插值到0。

而为了保持函数的不变,对距离标准进行如下调整:
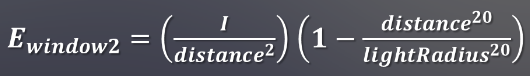
这个简单的方法可行,但会造成硬性的切断,看起来不自然。解决方式是用了一个阈值函数threshold对它进行重置到1,将其重新映射到初始范围0-1.(改进的光衰减 |我做错了 (wordpress.com))
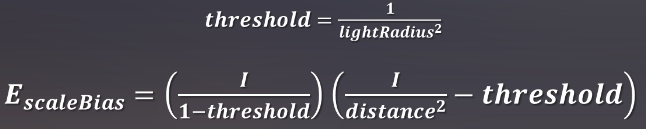
window2这样的结果较好,但这种方法的缺点是在0处有一个非零的梯度(下图第一个表的window2在变为0时斜率不为0),这会导致一个可见的不连续。更好的方法是对函数进行窗口化处理,并确保lightRadius处的梯度为0,这可以通过提高窗口函数的power来实现。

上图就是不同的窗口函数在不同的范围内的梯度变化。第1张图显示了不同的窗口函数,window2不连续,window3进行了平滑。第2、3张图显示了分别应用于光半径distance为10、40范围的窗口函数,它们的衰减范围falloff都是0~0.025。这表现了随着光半径的增加,曲线的拟合程度:

n允许我们调整过渡的平滑度。
寒霜引擎和Unity都采用了Window1的窗口函数,值n=4这个平滑函数已经被采用在所有的精确光和所有区域光上。由于lerp标准是径向的
![]()
,所以它不能很好的用于非球形的形状,如管型或矩形。
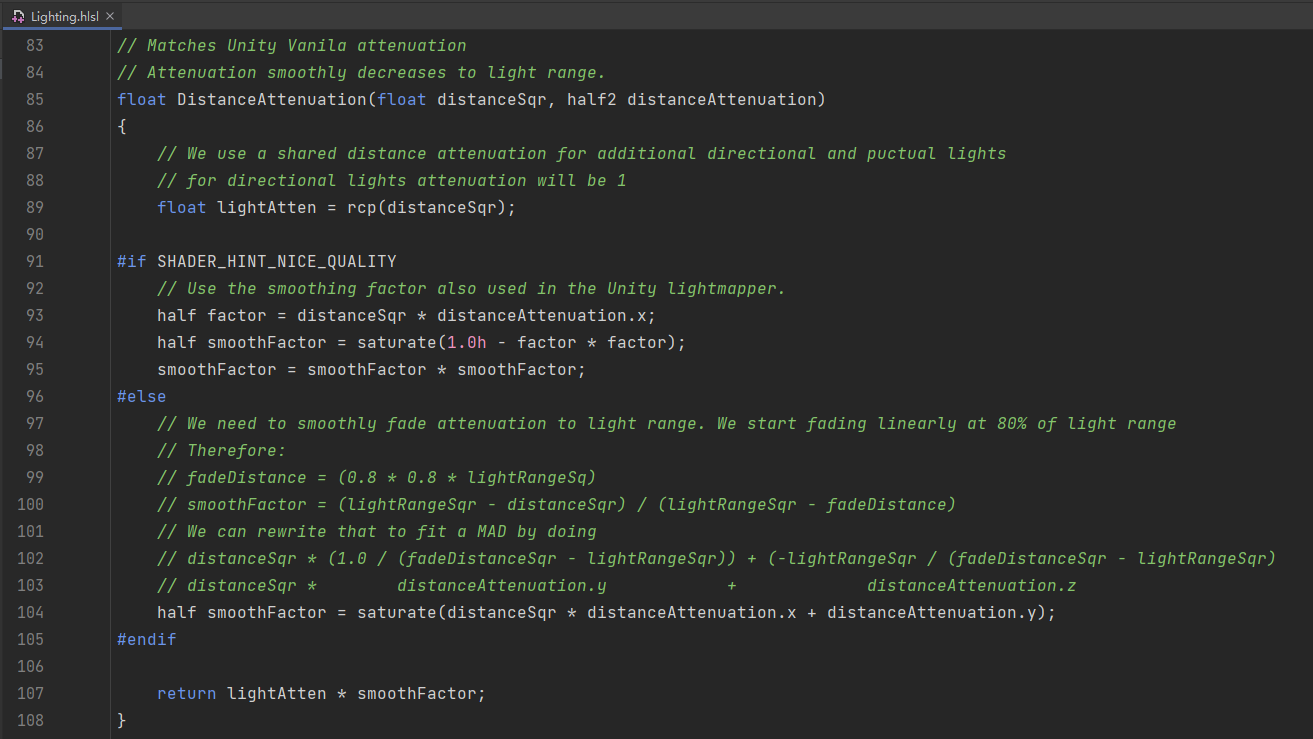
Unity的HDRP内精确光衰减计算:
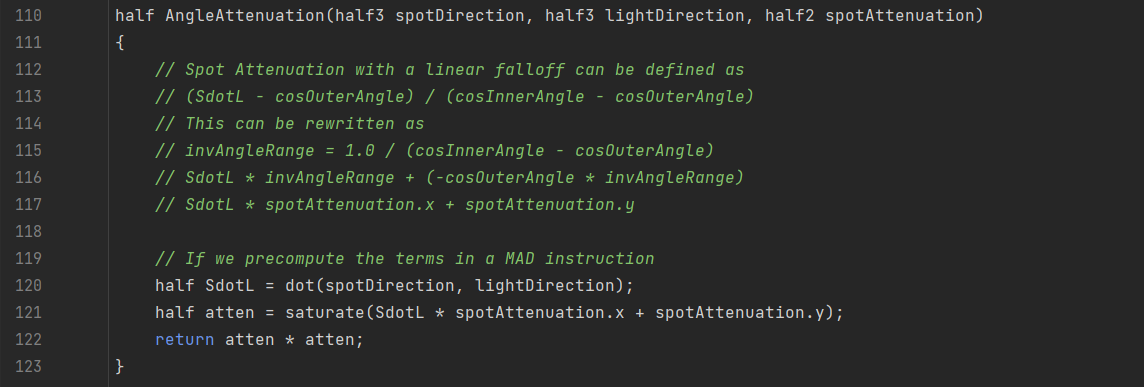
寒霜内精确光衰减计算:

它们的整体都是几乎是一样的。Unity的HDRP内精确光衰减计算调用部分:

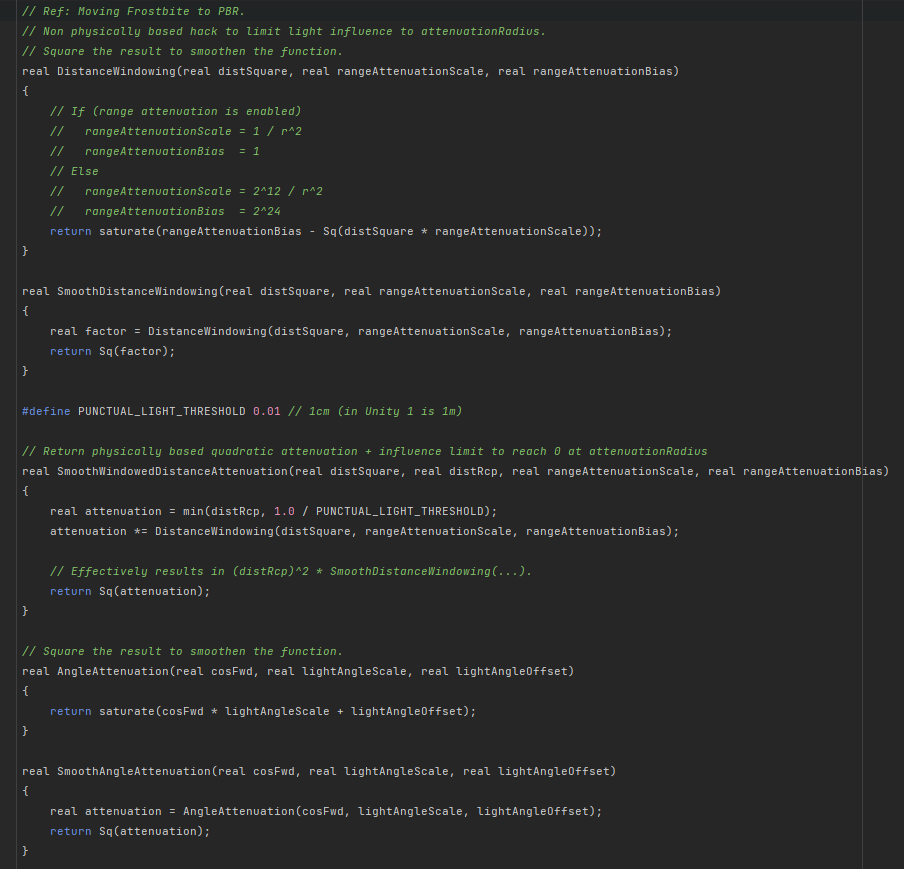
下图是基于物理的一个hack以限是光线对半径衰减的影响,平滑结果是一个平方函数。(这个hack就是下面链接它所表示的一个trick的方法:Improved light attenuation | I'm doing it wrong (wordpress.com))
3.2. IES
IES格式(Illuminating Engineering Society of NorthAmerica),成立于1906年,是一个以发展照明技术、科学和实践的技术学会,而以IES格式显示的配光电子文件,我们将其称为IES文件。
首先IES在略缩图的显示下,就是一个配光曲线图,如果用记事本的方式将它打开,就可以读取内部的数据。
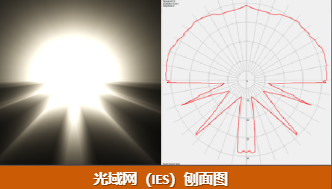
在Unity的HDRP中,IES 配置文件描述了光在给定方向上的传播方式。它们与光照剪影相似,都使用乘数遮罩来实现此目标。Unity IES 配置文件支持点光源、聚光灯(圆锥、棱锥和盒体形状)以及面(矩形)光源。

与光照剪影相比,使用 IES 配置文件的主要好处是由光源制造商提供这些配置文件。这意味着它们在物理上对于它们所代表的真实世界光线而言是准确的,并且美术师不需要花时间来创作它们。
可以将 IES 配置文件与光照剪影混合,甚至将配置文件和光照剪影混合以进行光照贴图烘焙。
IES是指使用光度轮廓来描述其强度分布,这些分布文件被存储在一个光度测量文件中。存在两种常见的格式:IES(.ies)和eulumdat(.lda)。在计算机图形学中,大多数都只支持IES格式,Unity和寒霜也不例外。
从IES文件创建的光度轮廓可以直接应用在一个点或聚光灯上,IES轮廓可用于描述光强,并可用一个乘法进行调整,这是控制具有发光强度的灯的唯一方法。
第二种选择是使用IES配置文件作为Mask,通过配置文件的最大强度进行归一化,为了用光强度点光方程处理这两种情况,我们根据其最大强度对轮廓进行归一化,然后光亮度计算如下:

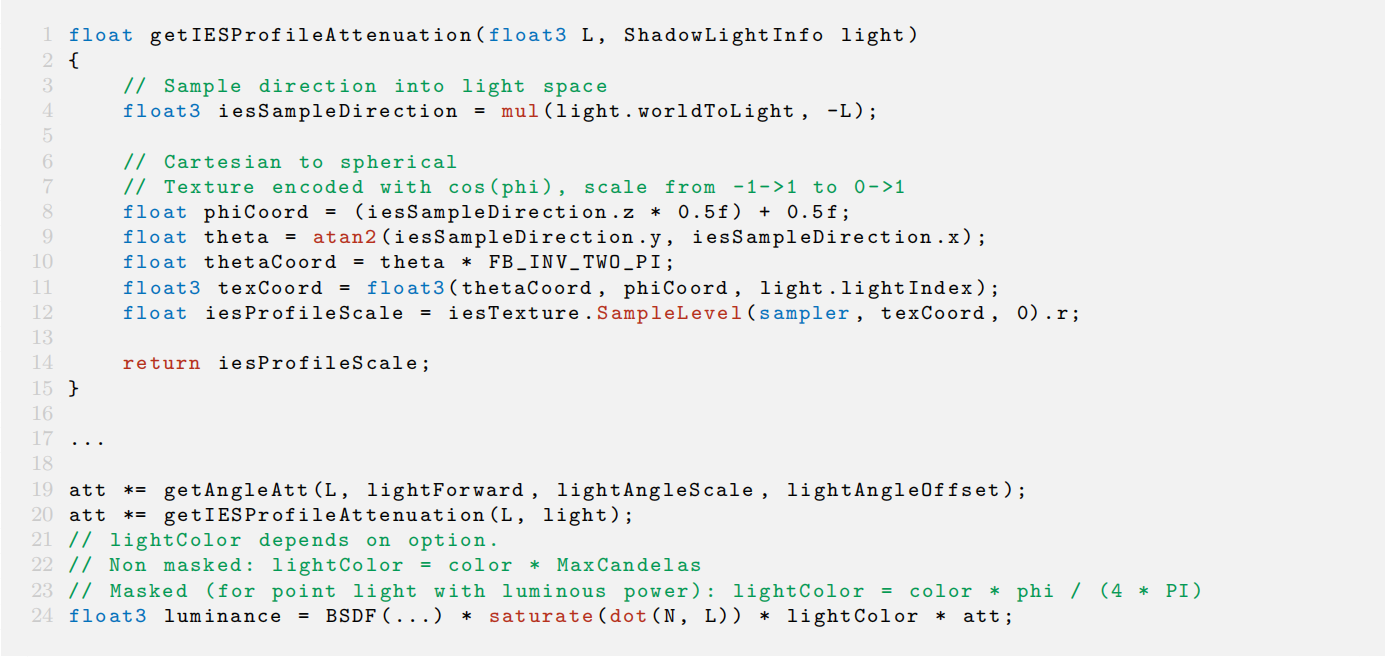
上述公式I代表轮廓的最大光强度,或者是用户定义的mask下的光强度。衰减函数getIESProfileAttenuatuin()返回的是归一化后的轮廓值。对于聚光灯角度衰减应用于这个等式之上,
什么意思呢?就是聚光灯要比点灯可以进行一些更好的处理,也可以进行更多的优化,对于剖面来说也比较方便。
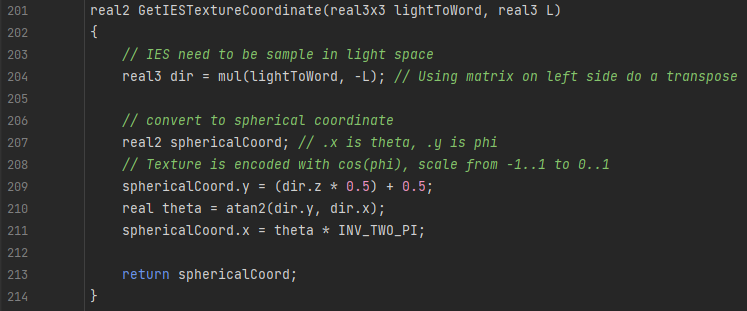
当创建一个新的光的轮廓时,球形光度函数会被重建并进行采样,填充一个球形参数化(θ,cosΦ),这个值是一个float2值。
如图是一个球形参数化,它的X值存储的是θ,y值存的是φ。我们存储按照最大强度倒数的缩放的归一化值,来处理使用mask和未使用mask。在着色器中,2d纹理会被计算并且作为衰减使用。
Unity-HDRP 内IES的计算
寒霜内IES的计算。
为什么要使用IES配置文件?
IES配置文件在室内设计中比在游戏中更有用。能够使用光配置文件作为Mask带来有趣的效果,比较方便应用,可以模拟复杂的光影效果,类似于cookie。下图左侧是IES渲染后的一个成品图。

上图右侧是在3dmax构建出来的IES的光域网。右下角就是它映射在墙上的一个关于网映射在墙上的形状。
3.3. 平行光 Sun
太阳是非常重要的光源,特别是对于户外环境,太阳对于方向的和照度变化非常敏感,将这样的光源作为材质漫反射部分的精确光是可以接受的近似。但对于镜面材质这样做会有问题。在寒霜引擎中,为了部分缓解这样的问题,将太阳视为了一个总是垂直于外半球的圆盘区域光,艺术家为垂直于太阳方向的表面指定太阳照度(以勒克斯为单位),下图是寒霜引擎直接使用的光表。
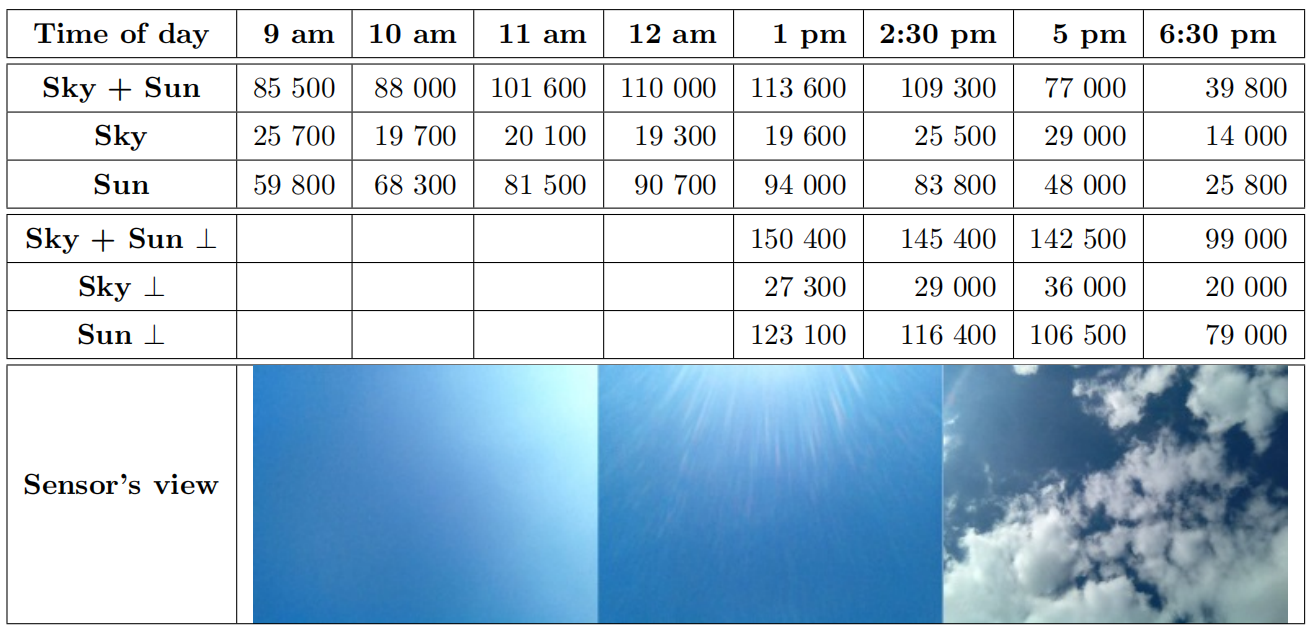
寒霜引擎内太阳的计算:

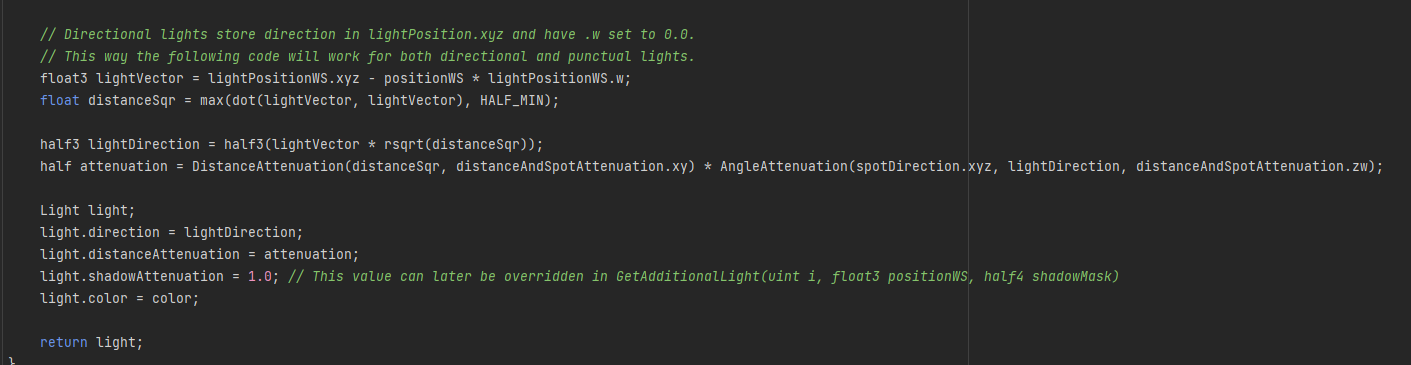
Unity引擎内对于太阳的计算和寒霜不确定是否一致,关于灯光参数的代码如下图所示,LightGUI面板上的光照度也是基于LUX的,但是是在Editor内就进行计算好的(不确定HDRP是否这样,没有细看,URP是这样,他们都是共用的一套Core,Unity内基于物理的天空计算代码在PhysicallyBasedSky.shader内,似乎也是使用了圆盘的区域光,感兴趣的同学可以自行翻阅。)
Unity-HDRP中关于灯光参数的代码。
在Lighting面板上,光照度它也是基于勒克斯Lux的。
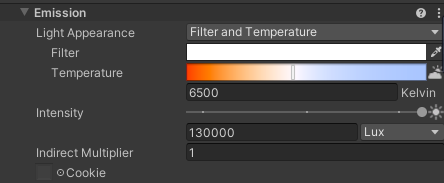
4. 灯光参数
物理灯装置 |高清晰度 RP |13.1.9 (unity3d.com)
灯光参数主要的是对于我们怎么去使用它。Unity光照和曝光图:
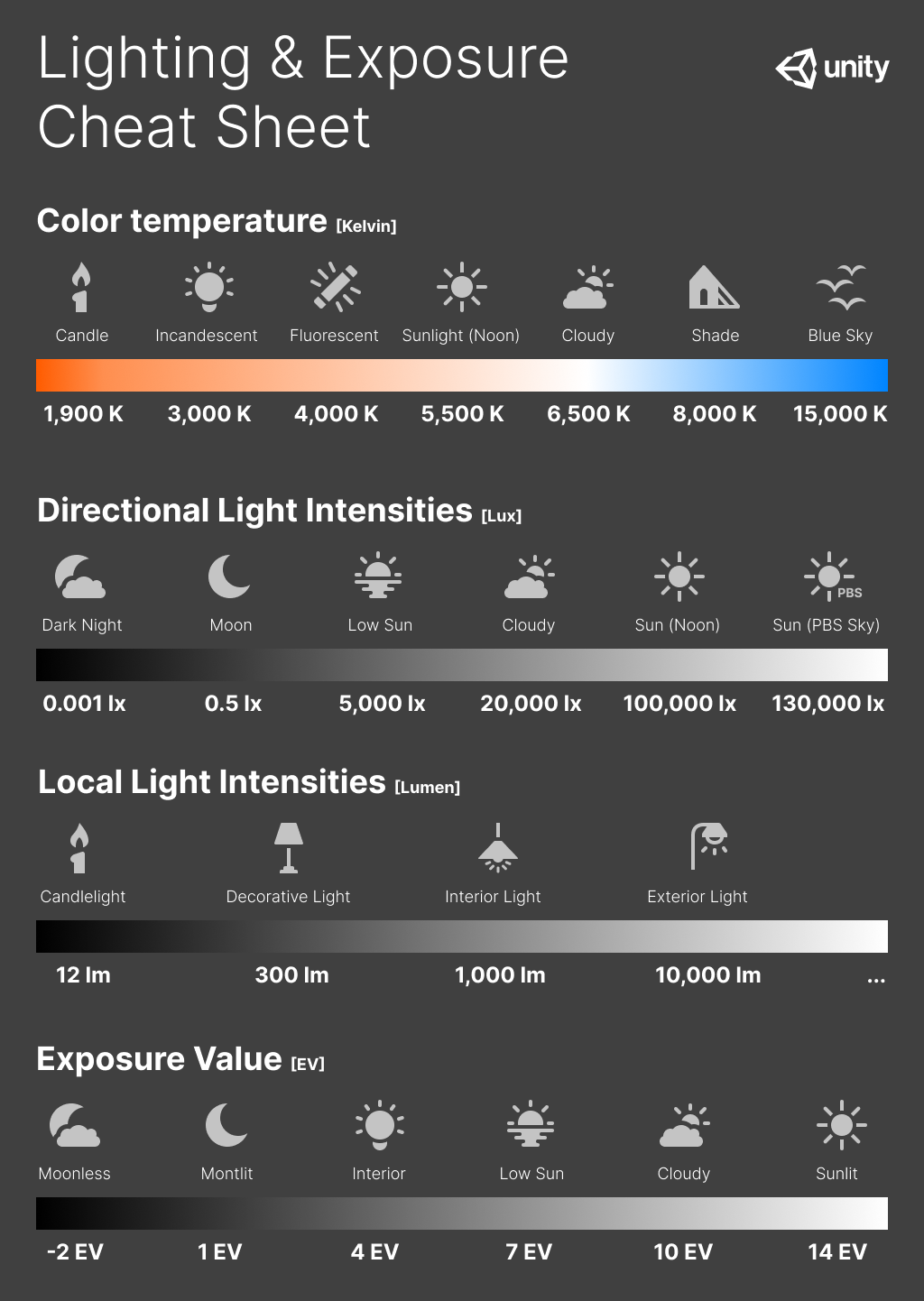
自然光、人造光和室内光推荐参数表:
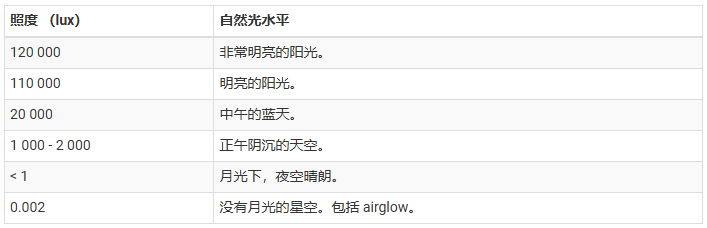
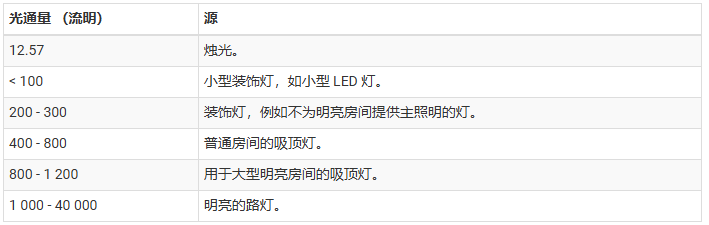
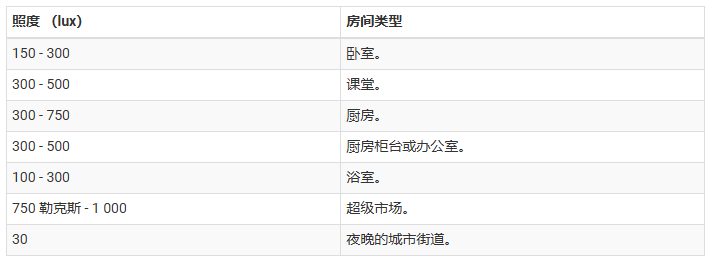
参考:
【译】【寒霜引擎】基于物理的渲染-物理的相机 - 知乎 (zhihu.com)
摄影中的光圈定义 |B&H eXplora (住宿加早餐旅馆) (bhphotovideo.com)
衍射_百度百科 (baidu.com)