大家好,这里是效率办公指南!
📚今天我们要探讨一个数学和编程领域中经常遇到的问题——矩阵特征值的计算方式,以及如何计算一个2x2矩阵的特征值。无论你是数学爱好者,还是编程高手,这个主题都可能对你有所帮助。
应用场景
矩阵特征值和特征向量的概念在多个领域都有重要的应用。以下是一些常见的应用场景:
物理学:在量子力学中,特征值问题用来描述粒子的能量状态。
工程学:在结构分析中,特征值分析用于确定结构的自然频率和模态。
计算机图形学:在3D建模中,特征值用于计算变换矩阵的缩放因子。
数据分析:主成分分析(PCA)中,特征值用于识别数据的主要变化方向。
机器学习:在算法中,如谱聚类,特征值用于数据点之间的相似度度量。
- 经济学:在经济模型中,特征值分析用于预测市场动态和经济周期。
计算方式
在数学中,矩阵的特征值是指满足方程 Av = λ v 的标量 λ,其中 A 是一个方阵,v 是一个非零向量,而 λ 被称为矩阵 A 的特征值,v 被称为对应的特征向量。
计算步骤
构造特征方程:对于一个 n x n 的矩阵 A,其特征方程为 det(A - λ I) = 0,其中 I 是单位矩阵,det 表示行列式。
求解特征方程:解上述方程,得到的解即为矩阵 A 的特征值。
计算特征向量:将每个特征值代入 Av = λ v,求解线性方程组,得到对应的特征向量。
计算示例
让我们以一个简单的2x2矩阵为例:
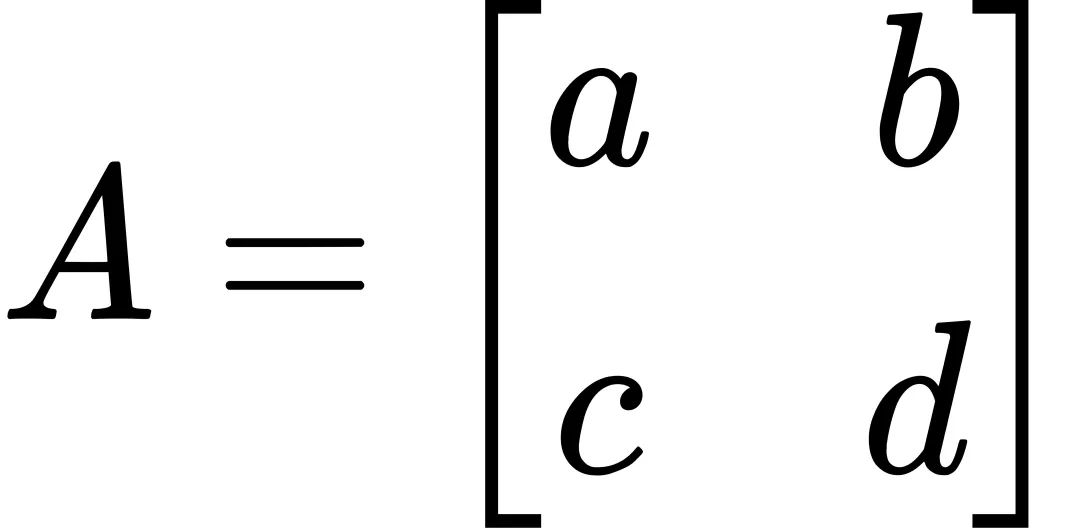
步骤1:构造特征方程
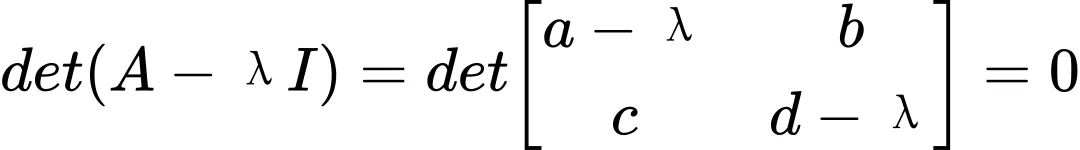
计算行列式:
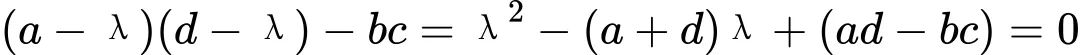
步骤2:求解特征方程
这是一个二次方程,我们可以使用求根公式来解它:
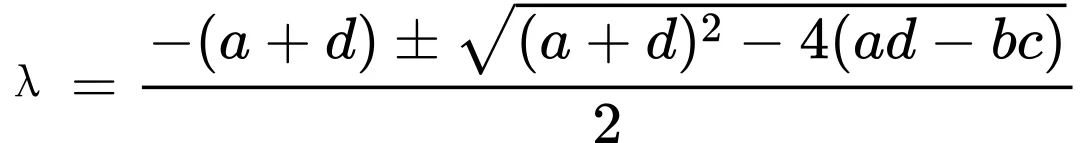
假设数据
矩阵A = {{1,2},{3,4}}
特征值 λ₁ = 1/2 (5 + √33)
特征值 λ₂ = 1/2 (5 - √33)
注意事项
确保矩阵是方阵,即行数和列数相等。
特征方程可能没有实数解,这种情况下,矩阵的特征值可能是复数。
- 在编程实现时,可以使用数值方法来求解特征方程,如幂法、QR算法等。
结语
矩阵的特征值和特征向量在许多领域都有广泛的应用,如线性代数、量子力学、图像处理等。掌握如何计算它们,无疑会为你的学习和工作带来便利。希望这篇文章能够帮助你更好地理解矩阵特征值的计算方式。如果你对这个话题有更多的兴趣,或者有其他问题,欢迎在下方留言,我们会尽快为你解答。
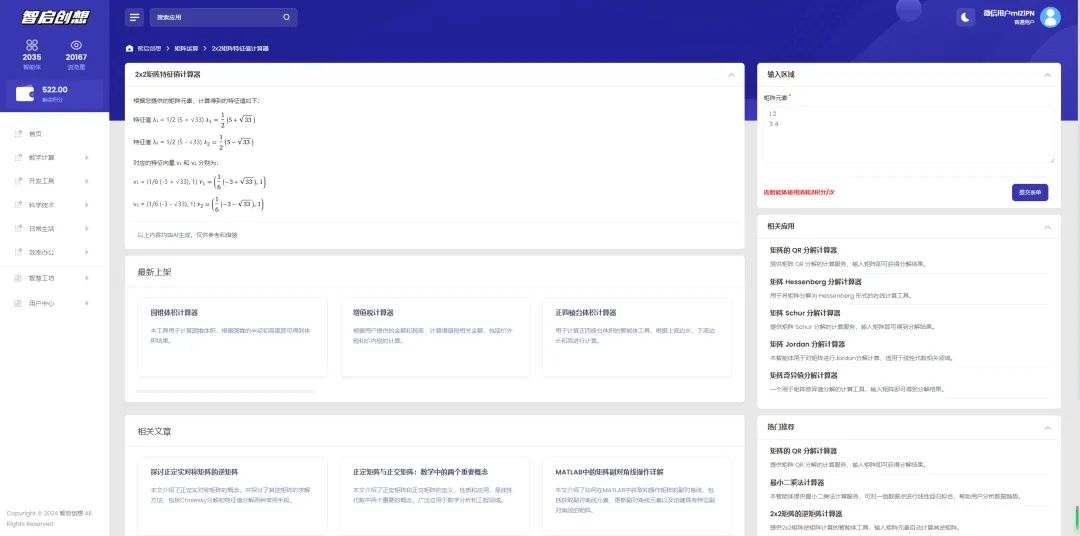
微信搜一搜【智启创想】,使用矩阵特征值计算器