前言：由于作者经常卡力扣周赛最后一题的dp，因此决定痛改前非，从头做人，争取下次能做出最后一道dp ak周赛！呜呜呜加油~~ 因此 这个系列的文章不会教 dp ，只会讲刷题思路，目前的计划是先更 lc 的题目，如果有时间也会做其他的 dp 问题

ps： 有些问题的最佳解决方式并非是 dp 思路，反之，这些题目的dp十分麻烦，这里直接给出简单解法！

目录

5、最长回文子串

10、正则表达式匹配

22、括号生成

32、最长有效括号

42、接雨水

44、通配符匹配

---

5、最长回文子串

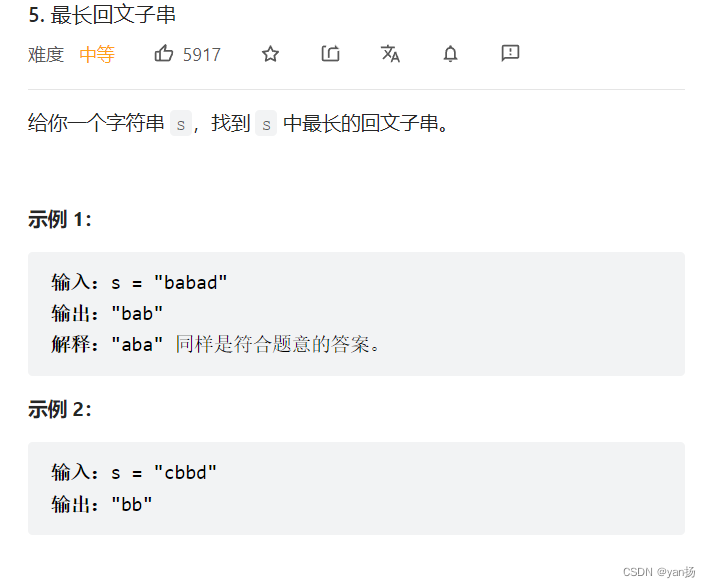
思路：这题通常的解法是用中心扩展法来解决，代码也比较简单，大家可以自行学习，这里仅仅介绍 dp 解法，f[i][j] 表示 i 到 j 是不是回文子串，转移的话， 就是 i 的字符 == j 的字符 并且 他们中间的字符串也要是 回文的（f[i + 1] [j - 1] == true || 长度 <= 3）dp 的顺序要按照拓扑序，所以我们必须先便利j，这样 我们的 f[i + 1][j - 1] 才是已经计算过的值 

class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        boolean[][] f = new boolean[n][n];
        String res = "";
        for (int j = 0; j < n; j ++) {
            for (int i = 0; i <= j; i ++) {
                if (i == j) f[i][j] = true;
                else if (s.charAt(i) == s.charAt(j)) {
                    if (j - i + 1 <= 3 || f[i + 1][j - 1]) f[i][j] = true; // 长度小于3也是 true
                }
                if (f[i][j] == true && j - i + 1 > res.length()) res = s.substring(i,j + 1);
            }
        }
        return res;
    }
}

10、正则表达式匹配

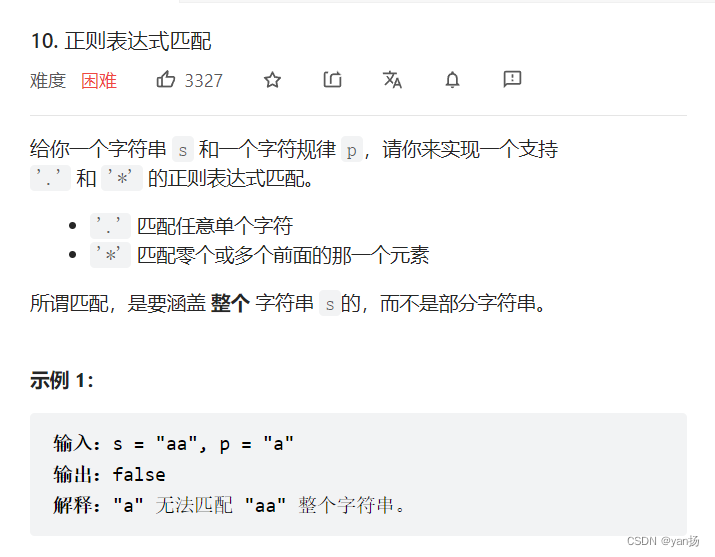
思路：

状态表示：f[i][j]表示p从j开始到结尾，是否能匹配s从i开始到结尾
状态转移：

如果p[j+1]不是通配符'*'，则f[i][j]是真，当且仅当s[i]可以和p[j]匹配，且f[i+1][j+1]是真；
如果p[j+1]是通配符'*'，则下面的情况只要有一种满足，f[i][j]就是真；
f[i][j+2]是真；
s[i]可以和p[j]匹配，且f[i+1][j]是真；
第1种情况下的状态转移很好理解，那第2种情况下的状态转移怎么理解呢？

最直观的转移方式是这样的：枚举通配符'*'可以匹配多少个p[j]，只要有一种情况可以匹配，则f[i][j]就是真；
这样做的话，我们发现，f[i][j]除了枚举0个p[j]之外，其余的枚举操作都包含在f[i+1][j]中了，所以我们只需判断
f[i+1][j]是否为真，以及s[i]是否可以和p[j]匹配即可。

时间复杂度分析：n 表示s的长度，m 表示p的长度，总共 nm 个状态，状态转移复杂度 O(1)，所以总时间复杂度是 O(nm)

class Solution {
    public boolean isMatch(String s, String p) {
        int n = s.length();
        int m = p.length();
        s = " " + s;
        p = " " + p;
        boolean[][] f = new boolean[n + 1][m + 1];
        f[0][0] = true;
        for (int i = 0; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
                if (j + 1 <= m && p.charAt(j + 1) == '*') continue;
                if (p.charAt(j) != '*') {
                    if (i > 0) f[i][j] = f[i - 1][j - 1] && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.');
                } else {
                    f[i][j] = f[i][j - 2] || i != 0 && f[i - 1][j] && (s.charAt(i) == p.charAt(j - 1) || p.charAt(j - 1) == '.');
                }
            }
        }
        return f[n][m];
    }
}

22、括号生成

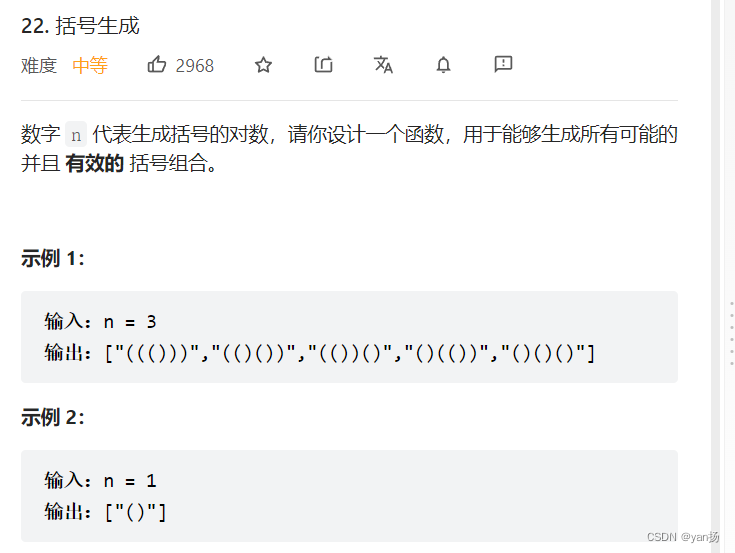
 思路：

1、dfs(int n,int l,int r,String s)：n表示最多有n个左括号和右括号，l表示左括号的个数，r表示右括号的个数，s表示当前的序列
2、若l < n，左括号的个数小于n，则可以在当前序列后面拼接左括号
3、若r < l，右括号的个数小于左括号的个数，则可以在当前序列后面拼接右括号

class Solution {
    List<String> res;
    public List<String> generateParenthesis(int n) {
        res = new ArrayList<>();
        dfs(n,0,0,"");
        return res;
    }

    public void dfs(int n,int lc,int rc,String path) {
        if (lc == n && rc == n) res.add(path);
        if (lc < n) dfs(n,lc + 1,rc, path + '(');
        if (rc < lc) dfs(n,lc,rc + 1, path + ')');
    }
}

 dp ? 压根不需要好吧！

32、最长有效括号

 

思路：

1、若当前元素是'('，则直接加入栈中
2、当当前元素是')'时，说明和栈顶元素有可能匹配
        1、若栈顶元素能和')'匹配，直接将栈顶元素pop出，则当前元素i与pop元素后的栈顶元素之间的长度是以i结尾的最长有效括号的长度
        2、若栈顶元素不能和')'匹配，则直接计算
注意：栈保存的是坐标（并且栈里存的只有左括号）

class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stk = new Stack();
        char[] arr = s.toCharArray();
        int res = 0;
        for (int i = 0,last = -1; i < arr.length; i ++) {
            if (arr[i] == '(') stk.push(i);
            else {
                if (stk.size() > 0) {
                    stk.pop();
                    if (stk.size() > 0) {
                        res = Math.max(res,i - stk.peek());
                    } else {
                        res = Math.max(res, i - last);
                    }
                }
                else {
                    last = i;
                }
            }
        }
        return res;
    }
}

42、接雨水

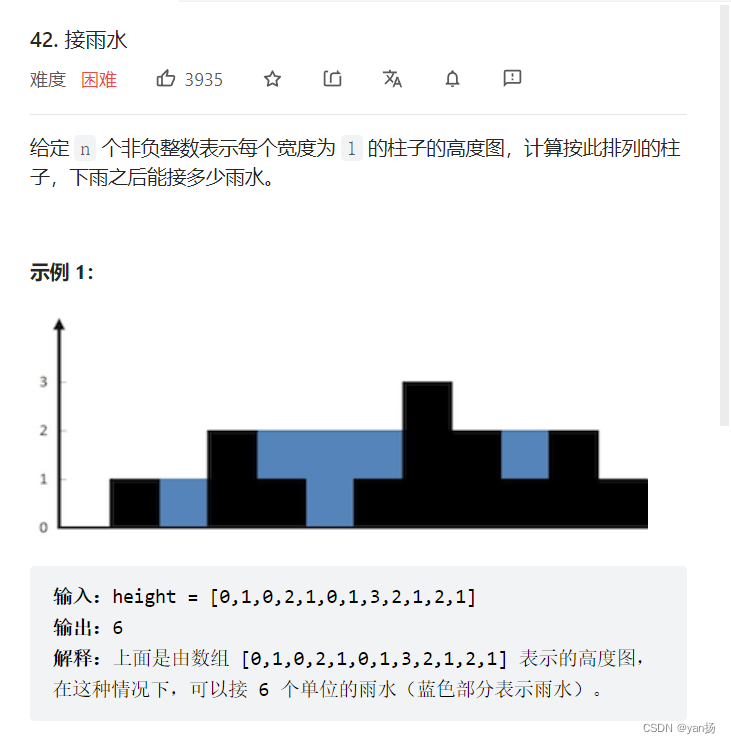
 思路：

对于数组中每个点，水有多高取决于这个点左侧和右侧墙壁的最大高度。第一个for循环找每个点的左侧最大高度，第二个for循环找每个点右侧的最大高度，循环中跳过最左侧(i=0)和最右侧点(i=nums.size()-1)的原因是这两个点由于没有左侧墙壁或右侧墙壁所以最大墙壁高度肯定是0，故在初始化nums的时候已经将其默认设置成0了。在得到所有点的左右墙壁最大高度后，木桶原理取左右墙壁较低的那个高度减去当前位置墙壁作为地面的高度就得到了这个位置上水的高度。然后将所有点的水高度相加即为解。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] l = new int[n];
        int[] r = new int[n];
        l[0] = height[0];
        l[n - 1] = height[n - 1];
        r[0] = height[0];
        r[n - 1] = height[n - 1];
        for (int i = 1; i < n - 1; i ++) l[i] = Math.max(l[i - 1],height[i]);
        for (int i = n - 2; i >= 1; i --) r[i] = Math.max(r[i + 1],height[i]);
        int res = 0;
        for (int i = 0; i < n; i ++) {
            res += Math.min(l[i],r[i]) - height[i];
        }
        return res;
    }
}

44、通配符匹配

 

class Solution {
    public boolean isMatch(String s, String p) {
        int n = s.length();
        int m = p.length();
        s = " " + s;
        p = " " + p;
        boolean[][] f = new boolean[n + 1][m + 1];
        f[0][0] = true;
        for (int i = 0; i <= n; i ++) {
            for (int j = 1; j <= m; j ++) {
               if (p.charAt(j) != '*') f[i][j] = i != 0 && f[i - 1][j - 1] && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '?');
               else {
                   f[i][j] = f[i][j - 1] || i != 0 && f[i - 1][j];
               } 
            }
        }
        return f[n][m];
    }
}

由于博主水平有限，分享之中不乏出现一些错误，欢迎大家指出讨论，我也会一一改进~~