目录
226.翻转二叉树
101. 对称二叉树
104.二叉树的最大深度
111.二叉树的最小深度
226.翻转二叉树
题目
226. 翻转二叉树 - 力扣(LeetCode)
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例1:
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]

示例2:
输入:root = []
输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
思路
视频讲解:LeetCode:226.翻转二叉树
代码随想录:226.翻转二叉树
想要翻转一颗二叉树,只需要把每一个节点的左右孩子都翻转一下,即可获得整体翻转的效果。
使用递归法时可以选择使用前序遍历或者后序遍历,前序遍历过程如下:
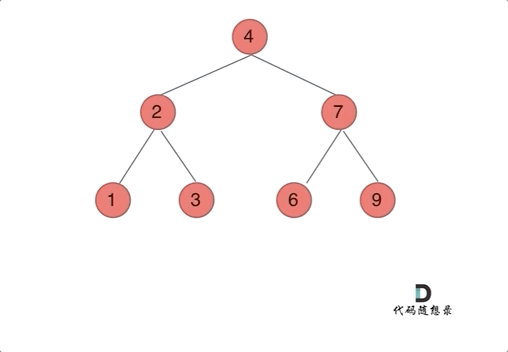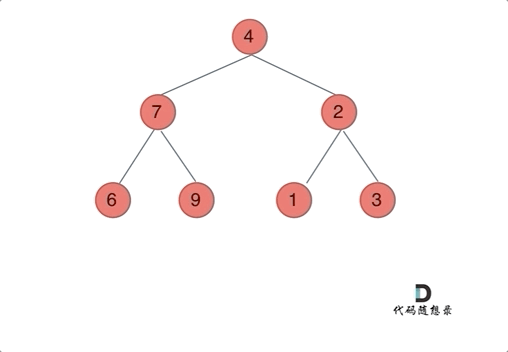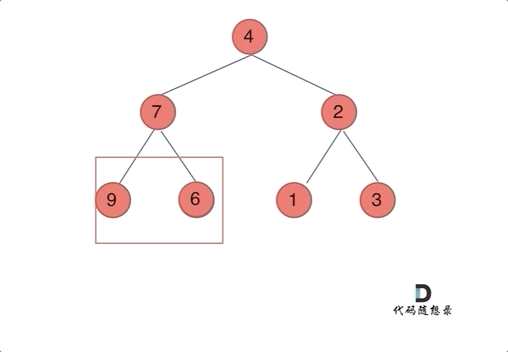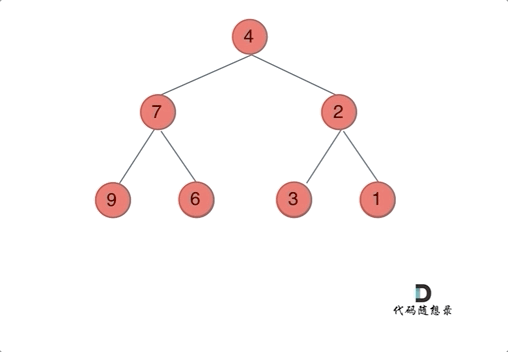
此外,还可以使用层序遍历。
题解
递归法:
class Solution {
public TreeNode invertTree(TreeNode root) {
return invert(root);
}
TreeNode invert(TreeNode root) {
if (root == null)
return root;
if (root.left != null)
invert(root.left);
if (root.right != null)
invert(root.right);
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
return root;
}
}
层序遍历:
class Solution {
public TreeNode invertTree(TreeNode root) {
Deque<TreeNode> deque = new ArrayDeque<>();
if (root == null)
return root;
deque.offer(root);
while (!deque.isEmpty()) {
int size = deque.size();
for (int i = 0; i < size; i++) {
TreeNode node = deque.poll();
TreeNode tmp = node.left;
node.left = node.right;
node.right = tmp;
if (node.left != null)
deque.offer(node.left);
if (node.right != null)
deque.offer(node.right);
}
}
return root;
}
}
101. 对称二叉树
题目
101. 对称二叉树 - 力扣(LeetCode)
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例1:
输入:root = [1,2,2,3,4,4,3]
输出:true
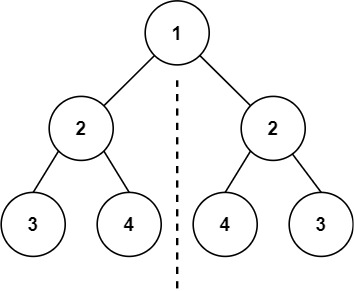
示例2:
输入:root = [1,2,2,null,3,null,3]
输出:false
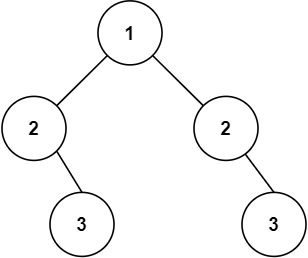
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
思路
代码随想录:101.对称二叉树
视频讲解:LeetCode:101. 对称二叉树
如果一棵二叉树是对称的,其根节点的左子树和右子树是镜像对称的,所以本题需要比较根节点的左右子树是否对称。
递归法:
- 先确定递归方法的参数为左子树和右子树中相对应的节点,返回值为布尔类型。
- 确定中止情况:左右两个节点都为空时,对称;左右两个节点其中一个为空时,不对称;左右两个节点值不同时,不对称。
- 比较两次,一次比较外侧的两个节点,一次比较内侧的两个节点。
迭代法:每次迭代时将左右两侧对应的节点一起放入队列中,每次取两个队列中的元素出来进行比较。
题解
递归法:
class Solution {
public boolean isSymmetric(TreeNode root) {
return compare(root.left, root.right);
}
boolean compare(TreeNode left, TreeNode right) {
if (left == null && right == null)
return true;
if ((left == null && right != null) || (left != null && right == null))
return false;
if (left.val != right.val)
return false;
boolean out = compare(left.left, right.right);
boolean in = compare(left.right, right.left);
return out == true && in == true;
}
}
迭代法:
class Solution {
public boolean isSymmetric(TreeNode root) {
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root.left);
deque.offer(root.right);
while (!deque.isEmpty()) {
TreeNode left = deque.poll();
TreeNode right = deque.poll();
if (left == null && right == null)
continue;
if (right == null || left == null || left.val != right.val)
return false;
deque.offer(left.left);
deque.offer(right.right);
deque.offer(left.right);
deque.offer(right.left);
}
return true;
}
}
104.二叉树的最大深度
题目
104. 二叉树的最大深度 - 力扣(LeetCode)
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例1:
输入:root = [3,9,20,null,null,15,7]
输出:3

思路
视频讲解:LeetCode:104.二叉树的最大深度
代码随想录:104.二叉树的最大深度
此题除了层序遍历之外,还可以使用递归法。
树的深度等于左子树深度和右子树深度中的最大值+1。
-
递归终止条件:当前节点为空。
-
找出返回值:节点为空时说明子树高度为 0,返回 0,节点不为空时则分别求左右子树的高度,取两者中的最大值加 1 表示当前节点的高度,返回该数值。
题解
层序遍历:
class Solution {
public int maxDepth(TreeNode root) {
int res = 0;
Deque<TreeNode> deque = new ArrayDeque<>();
if (root == null)
return res;
deque.offer(root);
while (!deque.isEmpty()) {
int size = deque.size();
for (int i = 0; i < size; i++) {
TreeNode node = deque.poll();
if (node.left != null)
deque.offer(node.left);
if (node.right != null)
deque.offer(node.right);
}
res++;
}
return res;
}
}
递归法:
class Solution {
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int left = maxDepth(root.left);
int right = maxDepth(root.right);
return Math.max(left, right) + 1;
}
}
}
111.二叉树的最小深度
题目
视频讲解:LeetCode:111.二叉树的最小深度
代码随想录:111.二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例1:
输入:root = [3,9,20,null,null,15,7]
输出:2

提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
思路
代码随想录:111.二叉树的最小深度
除了层序遍历,还可以使用递归法,对于每一个非叶子节点,分别计算其左右子树的最小叶子节点深度。
题解
层序遍历:
class Solution {
public int minDepth(TreeNode root) {
int res = 0;
Deque<TreeNode> deque = new ArrayDeque<>();
if (root == null)
return res;
deque.offer(root);
res++;
while (!deque.isEmpty()) {
int size = deque.size();
for (int i = 0; i < size; i++) {
TreeNode node = deque.poll();
if (node.left == null && node.right == null)
return res;
if (node.left != null)
deque.offer(node.left);
if (node.right != null)
deque.offer(node.right);
}
res++;
}
return res;
}
}
递归法:
class Solution {
public int minDepth(TreeNode root) {
if (root == null)
return 0;
if (root.left == null && root.right == null)
return 1;
int min = Integer.MAX_VALUE;
if (root.left != null)
min = Math.min(minDepth(root.left), min);
if (root.right != null)
min = Math.min(minDepth(root.right), min);
return min + 1;
}
}