Swift里的数值变量的最大值和最小值

news2024/11/16 8:31:06

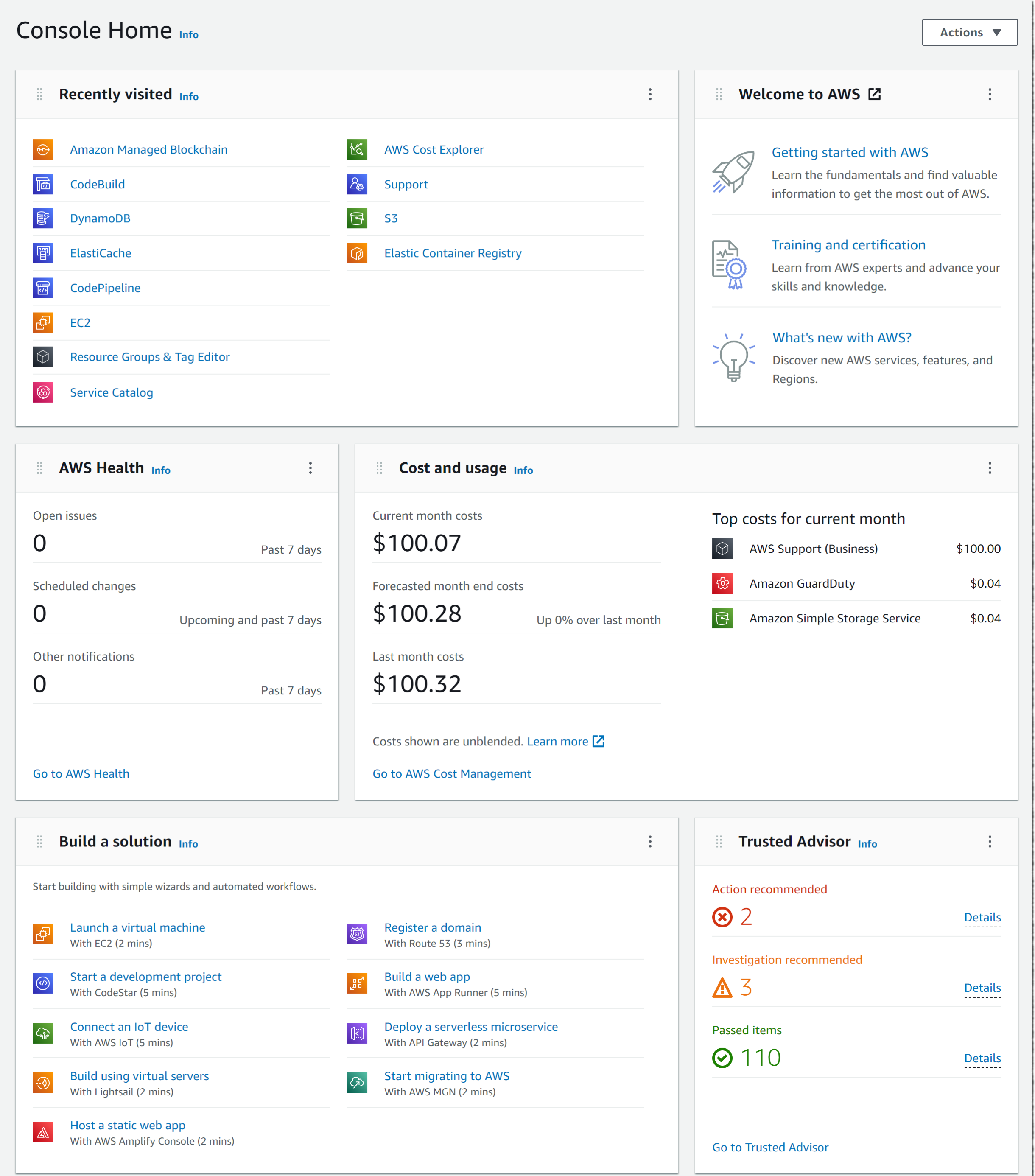
Swift里有很多种数值变量，如Int，Int8，Float，Double等。和绝大多数编程语言一样，由于是在计算机上运行，内存有限，所以必有最大值和最小值，而计算机无法处理超过该值的数。

在Swift中，数字变量类型都有一些静态属性，其固定值为该类变量的最大值和最小值。

一、整数型变量

（一）如何找到最大值和最小值

Swift里的整数型变量有Int，Int8，Int16，UInt等。这一类的变量，都可通过max，min来找到该类变量的最大值和最小值[1]。

print("Part 1: Integer bounds:\n")
var maxInt = Int.max //2^63-1
var minInt = Int.min //-2^63
print("The max Int is \(maxInt), and the min Int is \(minInt)")
var maxUInt = UInt.max //2^64-1
var minUInt = UInt.min //0
print("The max UInt is \(maxUInt), and the min UInt is \(minUInt)")
var maxInt8 = Int8.max
var minInt8 = Int8.min 
print("The max Int8 is \(maxInt8), and the min Int8 is \(minInt8)")

对于有符号整数类型，Int占64字节，Int32占32字节，以此类推。若该变量占字节数为 $a$ ，则其最大值为 $2^{a-1}-1$ ，最小值为 $-2^{a-1}$ 。对于无符号整数类型，UInt，UInt32等占字节数和有符号类型类似，但最大值为 $2^a-1$ ，最小值为 $0$ 。所以上述代码的运行输出为：

（二）超出最大值或最小值的溢出情况

我们知道，在C++中，如果出现了溢出现象，不会报错，而是会跳转至另一端。例如，对于int类型变量，最大值是2147483647，最大值+1就会计算出最小值-2147483648[2]。

#include <iostream> 
#include <string>
#include <climits>
using namespace std;
void main(){
    int num = INT_MAX;
    int too_big_num = num + 1;
    cout << "num=" << num << '\n';
    cout << "too_big_num=" << too_big_num;
}

上述代码运行输出为

那么在Swift中呢？

import Foundation

var num = Int.max
var too_big_num = num + 1
print("num=\(num)")
print("too_big_num=\(too_big_num)")

该程序运行会报错

这个错误是溢出错误。Swift不像C++，在处理整型变量时并不会在溢出时跳转到另一端。

那么，能不能用try ... catch的语句捕捉这个错误呢？

import Foundation

var num = Int.max
var too_big_num:Int?
do{
    too_big_num = try?(num + 1)
}
catch{
    print("Overflow")
}
print("num=\(num)")
print("too_big_num=\(too_big_num)")

该代码仍然无法运行，会报错。

原因在于，这样的溢出错误在Swift中属于FatalError。Swift的try ... catch机制无法处理FatalError[3]。有关Swift的错误捕获机制，请阅读[3]。

二、小数型变量

在Swift中，对于小数型变量，也就是Float和Double类型，不能像整型变量那样用max和min来得到最大值和最小值。但对于这一类变量，Swift里也定义了一些静态属性，表明它们的极限值[4]。

（一）小数型变量的极限值

小数型变量和整数型变量的区别在于小数型变量，即实数，从纯数学角度来看是连续的，也就是两个不同的实数中间总存在第三个实数[5]，即不存在相邻的两个实数。因此，数学上不存在最接近0的非零实数，但作为计算机编程语言，Swift不可能处理"无限接近"的概念。因此小数型变量的极限值有以下三种[4]。

（1）greatestFiniteMagnitude：Swift能处理的最大的绝对值，超过该值即为溢出。

（2）leastNormalMagnitude：Swift能处理的最小的正常态数，若小于该数，则Swift处理时无法保证精度。

（3）leastNonzeroMagnitude：Swift能处理的最小正数，也就是Swift能处理的不为零的绝对值最小值。

关于常态数（normal value）和非常态数（subnormal value）的区别，详见[6]。更具体的解释在[7]。简单地说，因为小数在计算机里表达的形式是 $x*2^y$ ，其中 $x$ 是一个用指定个数的bit表示的2进制小数（Float类型24位，Double类型53位），且规定只有第一位在小数点前； $y$ 是一个二进制表示的整数，Float类是-126～+128之间（8位），Double类是-1022～+1024之间（11位））。[7]中说Double类的指数最小-2046似乎不对，但也可能是Swift和别的语言不完全一样。而最小的正常态数是指 $x$ 首位为1的数中最小的数（此时 $y$ 已取最小值-126，而更小的数称为非常态数，所以计算精度会减小，因为 $x$ 首位不为1所以尾数（mantissa）的有效位数（significant bit）减少了[6]。

（二）比最大值更大或比最小值更小的溢出情况

在Swift中，对于小数型变量，即使溢出，也不会报错，而是会给出一个预留的特殊值。

如果绝对值超过最大值，则计为"无穷大"。如果绝对值小于最小值，则计为0。

print("\nPart 2: Floats and Doubles\n")
//But to get the greatest finite Float/Double, use this
var maxFloat = Float.greatestFiniteMagnitude
print("The max finite Float is \(maxFloat)")
var tooBigFloat = maxFloat * 1.1 //too big then infinity
print("If the Float is too big, then it becomes \(tooBigFloat)")
var tooBigFloat2 = Float.infinity //you can create infinity by a Swift function
print("Infinity can be created with Float.infinity. tooBigFloat2 = \(tooBigFloat2)")
var undef = tooBigFloat * 0 // 0*inf is undefined
print("0*inf is \(undef)")
var undef2 = Float.nan //you can create nan by a Swift function
// in addition, you can also find the smallest magnitude, which means that anything with absolute number smaller than this will be regarded as 0
var minFloat = Float.leastNonzeroMagnitude
print("The min non-zero Float is \(minFloat)")
var tooSmallFloat = minFloat / 2
print("If the Float is too small, then it becomes \(tooSmallFloat)")

运行输出为：

注意：Swift中对于Float和Double，存在inf（无穷大）和nan（未定义）。

（三）小于最小的常态数但不为0

正如前面说到的，非常态数的精度不如常态数。

下面的例子里，定义一个最小常态数minNormalDouble，再定义一个最小的非0数minDouble（小于minNormalDouble），然后把它们分别乘以1.01，观察结果是否能被判断出比原来大。

var maxDouble = Double.greatestFiniteMagnitude
print("The max finite Double is \(maxDouble)")
var minDouble = Double.leastNonzeroMagnitude
print("The least non-zero Double is \(minDouble)")
var minNormalDouble = Double.leastNormalMagnitude
print("The least normal Double is \(minNormalDouble)")

//How normal magnitude is different from non-zero magnitude?
print("\nPart 2.5: difference between normal and non-zero\n")
print("minDouble * 1.01 > minDouble? \(minDouble * 1.01 > minDouble)")

print("minNormalDouble * 1.01 > minNormalDouble? \(minNormalDouble * 1.01 > minNormalDouble)")

运行输出为：