代码随想录Day50|图论Part01，leetcode题目：98. 所有可达路径

news2024/12/28 21:11:14

提示：DDU，供自己复习使用。欢迎大家前来讨论~

文章目录

    • 图论理论基础Part01
      • 图的基本概念
      • 图的种类
    • 连通性
      • 连通图
      • 强连通图
      • 连通分量
      • 强连通分量
    • 图的构造
      • 邻接矩阵
      • 邻接表
    • 图的遍历方式
  • 深度优先搜索理论基础
    • DFS 与 BFS 区别
    • dfs 搜索过程
    • 代码框架
    • 深搜三部曲
      • 为什么需要回溯？
  • 题目
    • 题目一：98. 所有可达路径
      • 解题思路：
      • 邻接矩阵
      • 邻接表
    • 深度优先搜索
    • 打印结果
    • 本题代码
      • 邻接矩阵写法
      • 邻接表写法
  • 广度优先搜索理论基础
    • 广搜的使用场景
    • 广搜的过程
    • 代码框架

图论理论基础Part01

图的基本概念

二维坐标中，两点可以连成线，多个点连成的线就构成了图。

图的种类

连通性

在图中表示节点的连通情况，我们称之为连通性。

连通图

在无向图中，任何两个节点都是可以到达的，我们称之为连通图 ，如图：

img

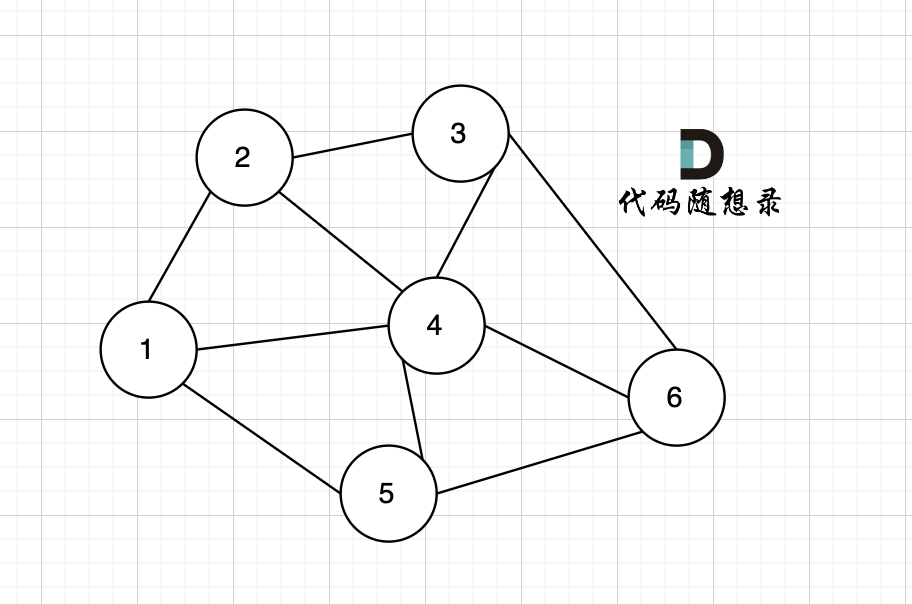
如果有节点不能到达其他节点，则为非连通图，如图：（节点1 不能到达节点4。）

img

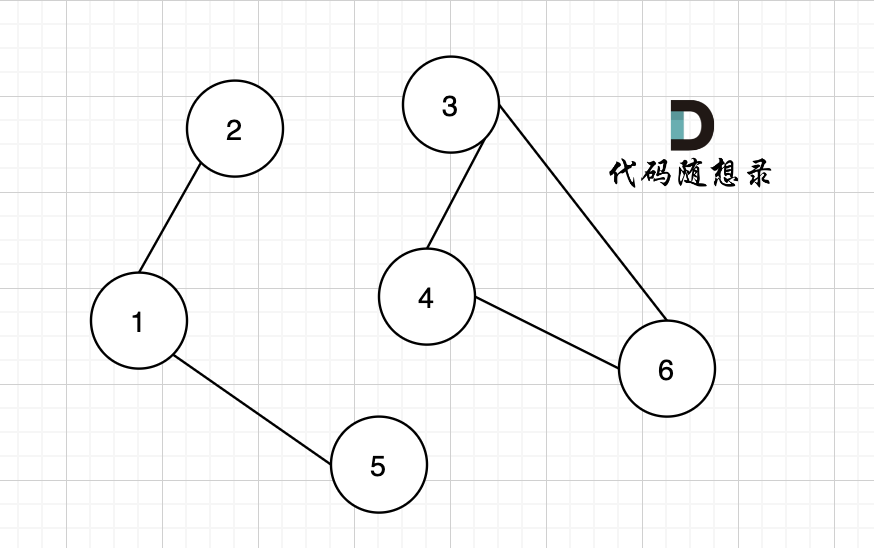
强连通图

在有向图中，任何两个节点是可以相互到达的，我们称之为 强连通图。

强连通图与无向图中的连通图的区别在于：

  1. 无向图的连通性：在无向图中，如果任意两个顶点之间都存在路径（可以是单向或双向的），则该图是连通的。在无向图中，连通性不区分方向。
  2. 有向图的强连通性：在有向图中，强连通性要求任意两个顶点之间都必须存在双向的路径，即从顶点A到顶点B，以及从顶点B到顶点A都存在路径。

第一个并不是强连通图，第二个是强连通图。

img img

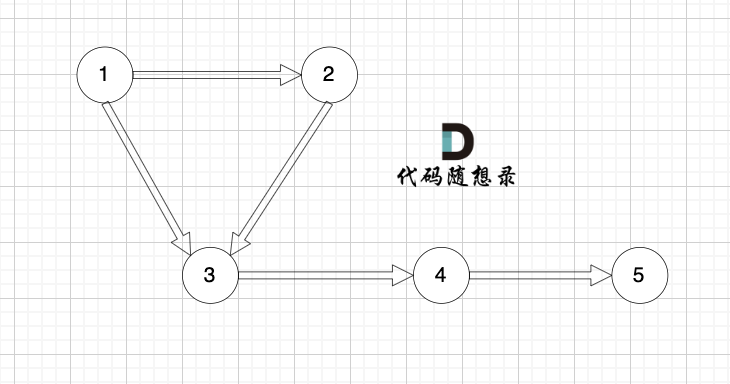
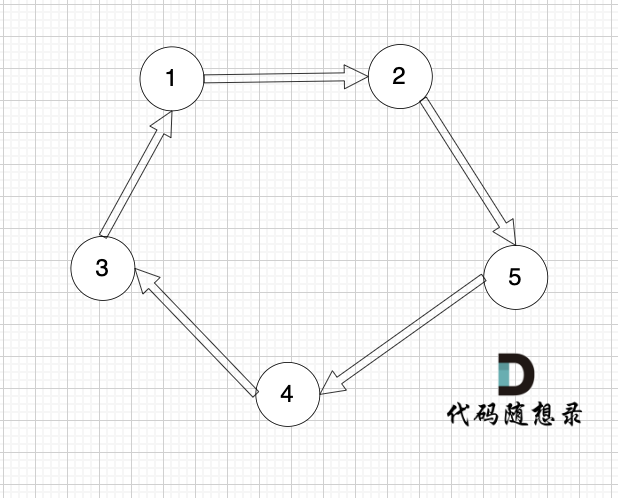
连通分量

在无向图中的极大连通子图称之为该图的一个连通分量。

img

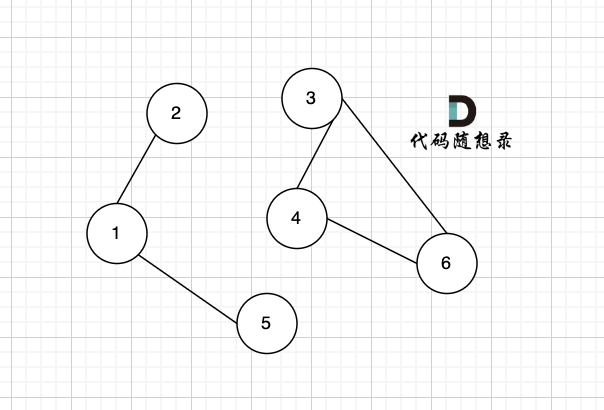
在无向图中，连通分量是指图中最大的、所有节点都相互可达的子图，只有包含所有相互可达节点的子图才能被称为极大连通分量。

在无向图中，只有包含所有相互可达节点的极大子图才能被称为连通分量。节点3和节点4构成的子图不是连通分量，因为它们没有包含所有相互可达的节点，而节点3、节点4和节点6构成的子图才是连通分量。

强连通分量

在有向图中极大强连通子图称之为该图的强连通分量。

img

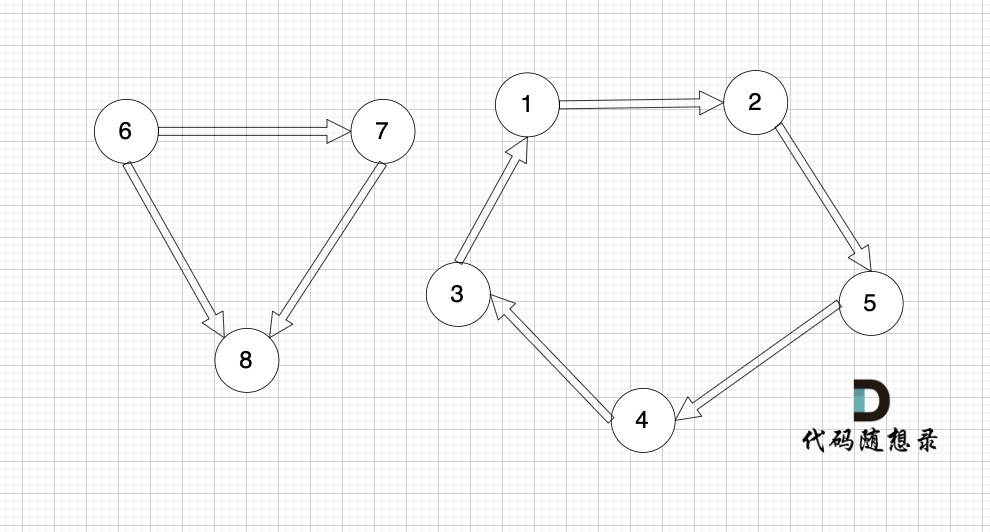
节点1、节点2、节点3、节点4、节点5 构成的子图是强连通分量，因为这是强连通图，也是极大图。

节点6、节点7、节点8 构成的子图 不是强连通分量，因为这不是强连通图，节点8 不能达到节点6。

节点1、节点2、节点5 构成的子图 也不是 强连通分量，因为这不是极大图。

图的构造

图的表示方法主要有以下几种：

  1. 邻接矩阵：这是表示图的一种简单方式，使用二维数组来存储图中的顶点和边。在这个矩阵中，索引代表顶点，而矩阵中的元素表示顶点之间的连接关系。如果两个顶点之间有边，则相应的矩阵元素为1（或边的权重），否则为0。邻接矩阵适用于稠密图，即边的数量接近顶点数量的平方。
  2. 邻接表：这是一种更节省空间的方法，特别是对于稀疏图（边的数量远小于顶点数量的平方）。在邻接表中，每个顶点对应一个列表，列表中包含与该顶点直接相连的所有顶点。这种方法可以有效地表示图的结构，并且便于遍历图中的边。
  3. 朴素存储：这是一种最基本的表示方法，通常用于教学或简单的图操作。在这种方法中，图的顶点和边可能直接以数组或列表的形式存储，没有明确的结构来表示连接关系。

邻接矩阵适合于稠密图和需要频繁检查两个顶点之间是否存在边的情况，而邻接表则更适合于稀疏图和需要频繁添加或删除边的情况。

邻接矩阵

邻接矩阵是一种用二维数组表示图的方法，其中数组的元素表示顶点间的连接关系和边的权重，对于无向图，如果节点2和节点5相连，那么数组中grid[2][5]和grid[5][2]都会被设置为相同的值，表示它们之间的双向连接和边的权重。

img

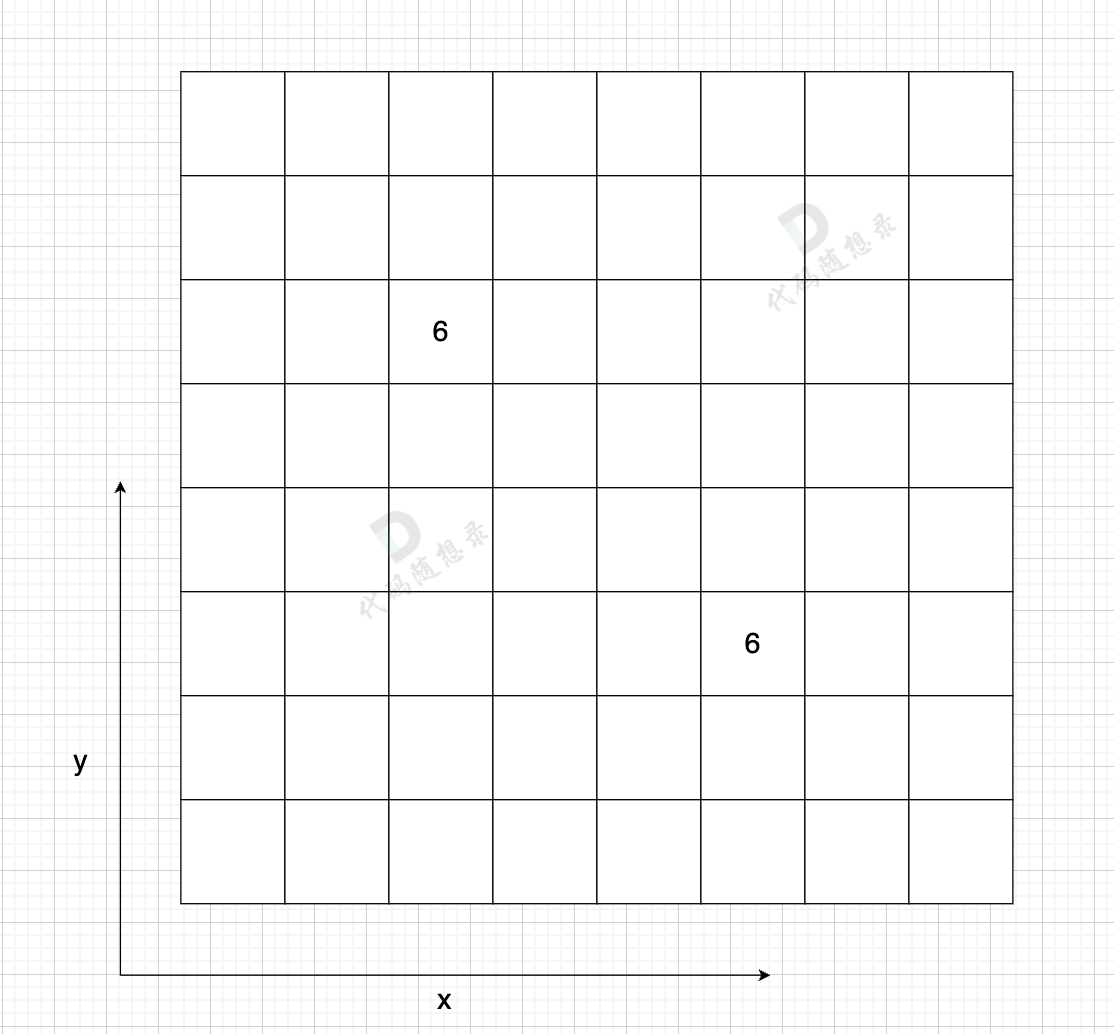
邻接矩阵是一种图的表示方法，它使用一个二维数组来存储节点间的连接关系和边的权重。对于无向图，如果节点i和节点j相连，则数组的第i行第j列和第j行第i列都会被设置为相应的权重值。

优点：

  • 表达直观，易于理解。
  • 快速检查任意两个顶点之间是否存在边。

缺点：

  • 在稀疏图中，会占用大量不必要的空间。
  • 遍历所有边时效率低，需要检查整个矩阵。

因此，邻接矩阵适合边数较多的稠密图，但在边数较少的稀疏图中可能会导致空间和时间上的浪费。

邻接表

邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图，有多少边 才会申请对应大小的链表。

在邻接表中，每个顶点对应一个链表，链表中存储的是与该顶点直接相连的其他顶点的信息，包括顶点标识和边的权重（如果有的话）。

邻接表的构造如图：

img

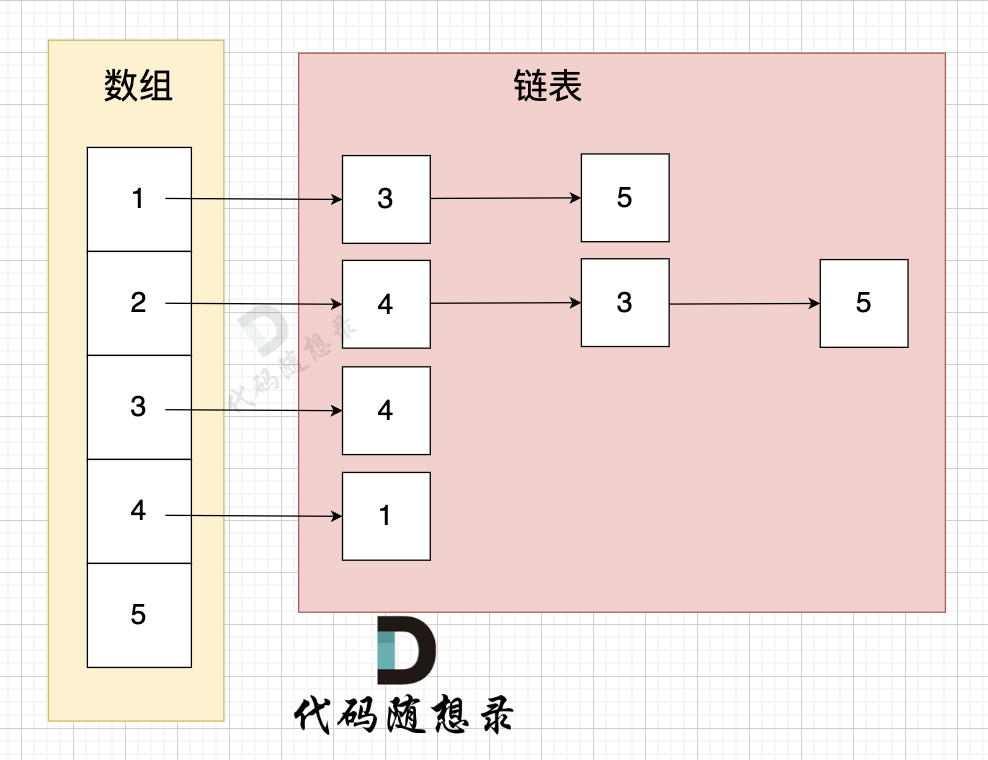
这里表达的图是：

  • 节点1 指向 节点3 和 节点5
  • 节点2 指向 节点4、节点3、节点5
  • 节点3 指向 节点4
  • 节点4指向节点1

有多少边 邻接表才会申请多少个对应的链表节点。

从图中可以直观看出 使用 数组 + 链表 来表达 边的连接情况 。

邻接表的优点：

  • 对于稀疏图的存储，只需要存储边，空间利用率高
  • 遍历节点连接情况相对容易

缺点：

  • 检查任意两个节点间是否存在边，效率相对低，需要 O(V)时间，V表示某节点连接其他节点的数量。
  • 实现相对复杂，不易理解

图的遍历方式

深度优先搜索（DFS）和广度优先搜索（BFS）是两种基本的图遍历算法，它们也可以应用于二叉树等其他数据结构。这两种算法在图论中用于探索图中的所有顶点，确保每个顶点都被访问一次。

深度优先搜索（DFS）：

  • 特点：尽可能深地搜索图的分支。
  • 实现：通常使用递归或栈来实现。
  • 应用：在二叉树上的递归遍历就是DFS的一种应用。

广度优先搜索（BFS）：

  • 特点：一层一层地搜索图的所有顶点。
  • 实现：通常使用队列来实现。
  • 应用：二叉树的层序遍历就是BFS的一种应用。

这两种算法不仅适用于二叉树，也适用于图结构，无论是使用邻接表还是邻接矩阵表示的图。DFS和BFS都是用于在图或树结构中进行系统搜索的算法，它们可以解决许多问题，如查找路径、检测环、确定图的连通分量等。

深度优先搜索理论基础

DFS 与 BFS 区别

  • 深度优先搜索（DFS）是沿着一个方向深入探索直到无法继续，然后回溯；
  • 而广度优先搜索（BFS）是逐层遍历节点，先访问所有相邻节点再逐层深入。

dfs 搜索过程

想象你正在探索一个迷宫，迷宫的每个房间通过门与其他房间相连。你的目标是找到从入口到出口的一条路径。

  1. 开始：你站在迷宫的入口房间（我们称之为“起点”）。
  2. 选择方向：你选择一扇门进入下一个房间（我们称之为“房间A”）。
  3. 深入探索：在房间A中，你再次选择一扇门进入下一个房间，继续这个过程，直到你到达一个没有门的房间（即“死胡同”）。
  4. 回溯：既然没有更多的门可以探索，你返回到上一个房间，选择另一扇未尝试的门，继续探索。
  5. 重复：你重复这个过程，每次深入探索新的路径，直到你找到出口或者探索完所有可能的路径。
  6. 找到出口：最终，你找到了通往出口的路径。

在这个例子中，深度优先搜索的过程就像你在迷宫中的行为：你总是尽可能深入地探索一条路径，直到无法再前进，然后返回并尝试其他路径，直到找到目标。这个过程可以用递归算法或使用栈的数据结构来实现。

代码框架

回顾一下回溯法的代码框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

回溯算法，其实就是dfs的过程，这里给出dfs的代码框架：

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

可以发现dfs的代码框架和回溯算法的代码框架是差不多的。

深搜三部曲

其实深搜也是一样的，深搜三部曲如下：

  1. 确认递归函数，参数
void dfs(参数)

通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。

一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。

例如这样：

vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)
  1. 确认终止条件

终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。

if (终止条件) {
    存放结果;
    return;
}

终止添加不仅是结束本层递归，同时也是我们收获结果的时候。

另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。

  1. 处理目前搜索节点出发的路径

一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

在深度优先搜索（DFS）中，"回溯"是一个关键的概念，它允许算法在探索完一条路径后返回到之前的节点，尝试其他可能的路径。这个过程是DFS能够探索所有可能路径的核心机制。

为什么需要回溯？

在DFS中，你从一个起始节点开始，沿着路径深入探索，直到达到一个没有未访问邻接节点的节点（即“死胡同”）。在这一点上，算法需要返回到上一个节点，尝试其他未探索的路径。这就是回溯的需要：它允许算法“撤销”之前的移动，以便探索其他可能的路径。

疑惑的地方，都是 dfs代码框架中for循环里分明已经处理节点了，那么 dfs函数下面 为什么还要撤销的呢。

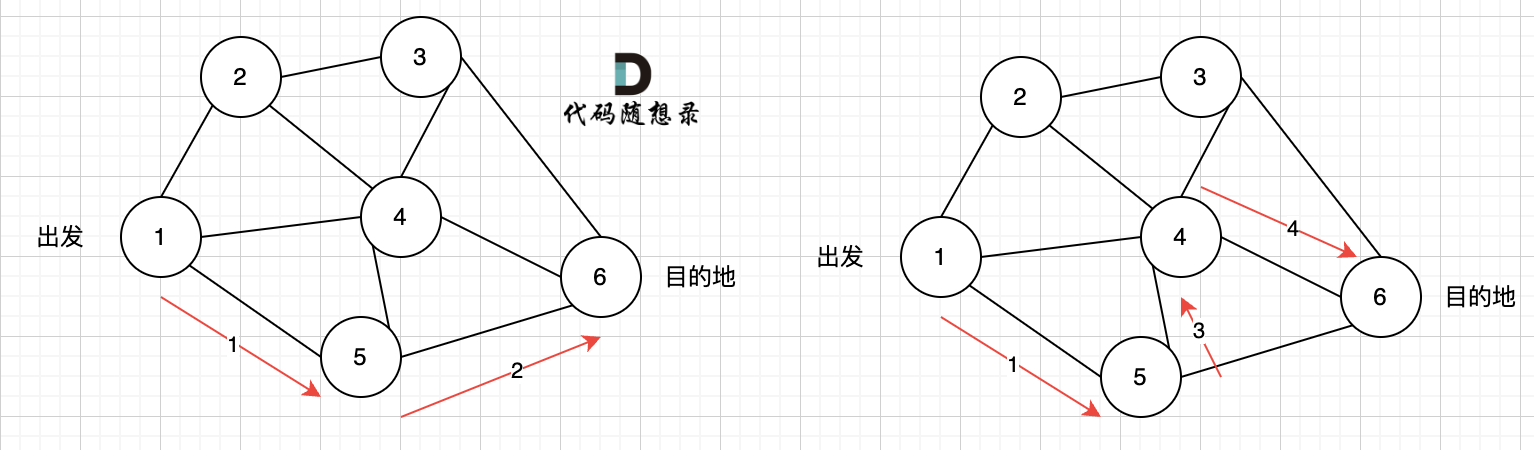
如图七所示， 路径2 已经走到了 目的地节点6，那么 路径2 是如何撤销，然后改为 路径3呢？

其实这就是 回溯的过程，撤销路径2，走换下一个方向。

图七

题目

题目一：98. 所有可达路径

  1. 所有可达路径

解题思路：

邻接矩阵

邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图，有多少节点就申请多大的二维数组。

本题我们会有n 个节点，因为节点标号是从1开始的，为了节点标号和下标对齐，我们申请 n + 1 * n + 1 这么大的二维数组。

vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));

输入m个边，构造方式如下：

while (m--) {
    cin >> s >> t;
    // 使用邻接矩阵 ，1 表示 节点s 指向 节点t
    graph[s][t] = 1;
}

邻接表

邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图，有多少边 才会申请对应大小的链表。

邻接表的构造相对邻接矩阵难理解一些。

img

这里表达的图是：

  • 节点1 指向 节点3 和 节点5
  • 节点2 指向 节点4、节点3、节点5
  • 节点3 指向 节点4
  • 节点4指向节点1

我们需要构造一个数组，数组里的元素是一个链表。

C++写法：

// 节点编号从1到n，所以申请 n+1 这么大的数组
vector<list<int>> graph(n + 1); // 邻接表，list为C++里的链表

输入m个边，构造方式如下：

while (m--) {
    cin >> s >> t;
    // 使用邻接表 ，表示 s -> t 是相连的
    graph[s].push_back(t);
}

本题我们使用邻接表 或者 邻接矩阵都可以，因为后台数据并没有对图的大小以及稠密度做很大的区分。

注意邻接表 和 邻接矩阵的写法都要掌握！

深度优先搜索

深搜三部曲来分析题目：

  1. 确认递归函数，参数

首先我们dfs函数一定要存一个图，用来遍历的，需要存一个目前我们遍历的节点，定义为x。

还需要存一个n，表示终点，我们遍历的时候，用来判断当 x==n 时候 标明找到了终点。

（其实在递归函数的参数 不容易一开始就确定了，一般是在写函数体的时候发现缺什么，参加就补什么）

至于 单一路径 和 路径集合 可以放在全局变量，那么代码是这样的：

vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 0节点到终点的路径
// x：目前遍历的节点
// graph：存当前的图
// n：终点
void dfs (const vector<vector<int>>& graph, int x, int n) {
  1. 确认终止条件

什么时候我们就找到一条路径了？

当目前遍历的节点 为 最后一个节点 n 的时候 就找到了一条 从出发点到终止点的路径。

// 当前遍历的节点x 到达节点n 
if (x == n) { // 找到符合条件的一条路径
    result.push_back(path);
    return;
}
  1. 处理目前搜索节点出发的路径

接下来是走 当前遍历节点x的下一个节点。

首先是要找到 x节点指向了哪些节点呢？ 遍历方式是这样的：

for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
    if (graph[x][i] == 1) { // 找到 x指向的节点，就是节点i
    }
}

接下来就是将 选中的x所指向的节点，加入到 单一路径来。

path.push_back(i); // 遍历到的节点加入到路径中来

进入下一层递归

dfs(graph, i, n); // 进入下一层递归

最后就是回溯的过程，撤销本次添加节点的操作。

该过程整体代码：

for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
    if (graph[x][i] == 1) { // 找到 x链接的节点
        path.push_back(i); // 遍历到的节点加入到路径中来
        dfs(graph, i, n); // 进入下一层递归
        path.pop_back(); // 回溯，撤销本节点
    }
}

打印结果

ACM格式大家在输出结果的时候，要关注看看格式问题，特别是字符串，有的题目说的是每个元素后面都有空格，有的题目说的是 每个元素间有空格，最后一个元素没有空格。

  1. 严格遵循题目要求：输出格式应与题目描述完全一致，包括空格、换行和标点符号。
  2. 元素间的空格：确保每个输出元素之间正确地添加或省略空格。
  3. 最后一个元素后的处理：
    • 有些题目要求在最后一个元素后不加空格。
    • 有些题目可能要求在最后一个元素后加空格。

例如示例输出是：

1 3 5` 而不是 `1 3 5

即 5 的后面没有空格！

以上代码中，结果都存在了 result数组里（二维数组，每一行是一个结果），最后将其打印出来。（重点看注释）

// 输出结果
if (result.size() == 0) cout << -1 << endl;
for (const vector<int> &pa : result) {
    for (int i = 0; i < pa.size() - 1; i++) { // 这里指打印到倒数第二个
        cout << pa[i] << " ";
    }
    cout << pa[pa.size() - 1]  << endl; // 这里再打印倒数第一个，控制最后一个元素后面没有空格
}

本题代码

邻接矩阵写法

#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 1节点到终点的路径

void dfs (const vector<vector<int>>& graph, int x, int n) {
    // 当前遍历的节点x 到达节点n 
    if (x == n) { // 找到符合条件的一条路径
        result.push_back(path);
        return;
    }
    for (int i = 1; i <= n; i++) { // 遍历节点x链接的所有节点
        if (graph[x][i] == 1) { // 找到 x链接的节点
            path.push_back(i); // 遍历到的节点加入到路径中来
            dfs(graph, i, n); // 进入下一层递归
            path.pop_back(); // 回溯，撤销本节点
        }
    }
}

int main() {
    int n, m, s, t;
    cin >> n >> m;

    // 节点编号从1到n，所以申请 n+1 这么大的数组
    vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));

    while (m--) {
        cin >> s >> t;
        // 使用邻接矩阵 表示无线图，1 表示 s 与 t 是相连的
        graph[s][t] = 1;
    }

    path.push_back(1); // 无论什么路径已经是从0节点出发
    dfs(graph, 1, n); // 开始遍历

    // 输出结果
    if (result.size() == 0) cout << -1 << endl;
    for (const vector<int> &pa : result) {
        for (int i = 0; i < pa.size() - 1; i++) {
            cout << pa[i] << " ";
        }
        cout << pa[pa.size() - 1]  << endl;
    }
}

邻接表写法

#include <iostream>
#include <vector>
#include <list>
using namespace std;

vector<vector<int>> result; // 收集符合条件的路径
vector<int> path; // 1节点到终点的路径

void dfs (const vector<list<int>>& graph, int x, int n) {

    if (x == n) { // 找到符合条件的一条路径
        result.push_back(path);
        return;
    }
    for (int i : graph[x]) { // 找到 x指向的节点
        path.push_back(i); // 遍历到的节点加入到路径中来
        dfs(graph, i, n); // 进入下一层递归
        path.pop_back(); // 回溯，撤销本节点
    }
}

int main() {
    int n, m, s, t;
    cin >> n >> m;

    // 节点编号从1到n，所以申请 n+1 这么大的数组
    vector<list<int>> graph(n + 1); // 邻接表
    while (m--) {
        cin >> s >> t;
        // 使用邻接表 ，表示 s -> t 是相连的
        graph[s].push_back(t);

    }

    path.push_back(1); // 无论什么路径已经是从0节点出发
    dfs(graph, 1, n); // 开始遍历

    // 输出结果
    if (result.size() == 0) cout << -1 << endl;
    for (const vector<int> &pa : result) {
        for (int i = 0; i < pa.size() - 1; i++) {
            cout << pa[i] << " ";
        }
        cout << pa[pa.size() - 1]  << endl;
    }
}

广度优先搜索理论基础

广搜（bfs）是一圈一圈的搜索过程，和深搜（dfs）是一条路跑到黑然后再回溯。

广搜的使用场景

广搜的搜索方式就适合于解决两个点之间的最短路径问题。

因为广搜是从起点出发，以起始点为中心一圈一圈进行搜索，一旦遇到终点，记录之前走过的节点就是一条最短路。

当然，也有一些问题是广搜 和 深搜都可以解决的，例如岛屿问题，这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行。

广搜的过程

广度优先搜索（BFS）是一种图遍历算法，它从一个起始节点开始，逐层（或一圈一圈）地向外扩展，直到找到目标节点或遍历完所有可达节点。BFS常用于在无权图中找到从起点到终点的最短路径。

BFS的特点：

  1. 逐层搜索：BFS从起点开始，先访问所有直接相邻的节点（第一层），然后访问这些节点的相邻节点（第二层），依此类推。
  2. 使用队列：BFS通常使用队列数据结构来管理待访问的节点，确保按照广度优先的顺序进行访问。
  3. 最短路径：由于BFS按层次遍历，一旦找到终点，它所经过的路径必然是最短的。

简单例子： 假设你在一个5x5的网格地图上，从左上角（0,0）位置开始，目标是到达右下角（4,4）位置。地图中的每个格子可以向上、下、左、右移动，但不能斜着移动。

  1. 起点：从（0,0）开始，你可以向四个方向（上、下、左、右）移动。
  2. 第一层：你移动到（0,1）、（1,0）、（0,-1）、（-1,0）。
  3. 第二层：然后，你从这四个新位置继续向四个方向移动，覆盖更多的格子。
  4. 重复：这个过程不断重复，直到你到达（4,4）或者所有可达的格子都被访问过。

在这个过程中，BFS会记录每个节点的前一个节点，这样一旦到达终点，就可以通过这些记录回溯到起点，形成一条完整的路径。

总结： BFS是一种有效的图遍历算法，特别适用于在无权图中寻找最短路径。它通过逐层搜索和使用队列来管理待访问的节点，确保每个节点都被访问且只被访问一次。一旦找到目标节点，就可以通过回溯确定最短路径。

代码框架

广度优先搜索（BFS）的“一圈一圈”搜索过程是通过使用合适的数据结构来实现的，主要目的是保证搜索的顺序性和系统性。以下是关键点的总结：

  1. 容器选择：可以使用队列、栈或数组来实现BFS。每种数据结构都会影响搜索的顺序。
  2. 队列：
    • 特点：先进先出（FIFO）。
    • 搜索顺序：保持一致的方向（如总是顺时针或逆时针）。
    • 原因：队列保证了元素的加入和弹出顺序一致，使得搜索过程可以系统地逐层进行。
  3. 栈：
    • 特点：先进后出（LIFO）。
    • 搜索顺序：可能在每一层改变方向（如第一层顺时针，第二层逆时针）。
    • 原因：栈的后进先出特性使得搜索可以在每一层改变方向。
  4. 数组：
    • 特点：静态存储，需要额外的逻辑来控制搜索顺序。
    • 搜索顺序：需要手动管理，可能不如队列和栈直观。
  5. 广度优先搜索的顺序：
    • 重要性：对于找到最短路径，搜索的顺序并不重要，因为BFS保证一旦找到目标，它就是最短路径。
    • 习惯：尽管使用栈也可以实现BFS，但使用队列更为常见，因为它直观地支持逐层搜索。尽管理论上可以使用队列、栈或数组来实现BFS，但队列是最常用的选择，因为它自然地支持逐层、系统性地搜索。

下面给出广搜代码模板，该模板针对的就是，上面的四方格的地图： （详细注释）

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/2151331.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Superset 使用指南之优化数据可视化性能与扩展

Superset 使用指南之优化数据可视化性能与扩展

1. Superset 概述 什么是 Apache Superset&#xff1f; Apache Superset 是一个开源、现代化的数据可视化和数据探索平台。它通过提供直观的用户界面&#xff0c;使用户能够轻松创建复杂的图表和仪表板&#xff0c;探索海量数据&#xff0c;同时避免传统商业智能&#xff08;…
阅读更多...
Apache James配置连接达梦数据库

Apache James配置连接达梦数据库

项目场景&#xff1a; Apache James配置连接达梦数据库&#xff0c;其他配置中不存在的数据库也可参考此方案。 配置步骤 1、把需要的jar包导入到James 把DmJdbcDriver18.jar复制到下面lib目录下 james-2.3.2\lib 2、 修改连接配置 james-2.3.2\apps\james\SAR-INF\confi…
阅读更多...
k8s部署jenkins集群时，使用ThinBackup进行定期备份

k8s部署jenkins集群时，使用ThinBackup进行定期备份

一、背景 使用k8s部署jenkins集群的时候&#xff0c;一般会把$JENKSIN_HOME&#xff08;默认是/var/jenkins_home&#xff09;进行持久化。 volumeMounts:- name: jenkins-homemountPath: /var/jenkins_home这样&#xff0c;机器重启&#xff0c;保证不会丢失文件。 本文要讲…
阅读更多...
杀死端口占用的进程

杀死端口占用的进程

1、查看端口的进程&#xff0c;以9023为例 &#xff08;1&#xff09;方法1 netstat -tunpl|grep 9023 &#xff08;2&#xff09;方法2 ss -tulpan |grep 9023 &#xff08;3&#xff09;方法3 netstat -ntlp |grep 9023 &#xff08;4&#xff09;方法4 lsof -i:9023 …
阅读更多...
Linux：虚拟文件系统/proc和self进程

Linux：虚拟文件系统/proc和self进程

相关阅读 Linuxhttps://blog.csdn.net/weixin_45791458/category_12234591.html?spm1001.2014.3001.5482 /proc目录 在Linux操作系统中&#xff0c;目录/proc是一个虚拟文件系统&#xff0c;称为procfc&#xff0c;用于访问内核和系统的实时状态信息。这个文件系统不同于常规…
阅读更多...
下载 B 站封面的正确方式

下载 B 站封面的正确方式

B 友们经常用一些很好看的图片作为视频封面&#xff0c;但是大部分都不会指出图片来源&#xff0c;为此我们可以下载封面原图&#xff0c;用于保存或者搜索源出处。 这里介绍几个我知道的方法&#xff0c;欢迎补充&#x1f914; ‍ 使用相关客户端 上一篇博客介绍了很多的能…
阅读更多...
基于微型5G网关的酒店服务机器人应用

基于微型5G网关的酒店服务机器人应用

智能机器人在酒店中已经越来越常见&#xff0c;并且也是提升客户体验、提高服务效率的重要工具。然而&#xff0c;尽管这些机器人在自动化服务方面可以发挥着重要作用&#xff0c;但它们仍然面临着一些通信、组网和在线管理方面的痛点。 针对这些难题&#xff0c;可以通过部署微…
阅读更多...
【数据结构入门】排序算法之三路划分与非比较排序

【数据结构入门】排序算法之三路划分与非比较排序

文章目录 前言 一、三路划分优化 1.1. 基本思想 1.2. 实现步骤 1.3. 优点 1.4 代码实现 二、非比较排序 2.1 计数排序 2.1.1基本思想 2.1.2具体步骤 2.1.3算法特性 2.1.4算法实现 2.2 基数排序 2.2.1基本思想 2.2.2具体步骤 2.2.3 基数排序的方法 2.2.4算法特…
阅读更多...
【高等代数笔记】线性空间（五-九）

【高等代数笔记】线性空间（五-九）

3. 线性空间 主线任务&#xff1a;研究线性空间和它的子空间的结构 研究平面 π \pi π上向量共线与不共线的问题&#xff1a; c ⃗ \vec{c} c 与 a ⃗ ≠ 0 \vec{a}\ne\boldsymbol{0} a 0共线 c ⃗ λ a ⃗ ⇔ λ ∈ R ⇔ − λ a ⃗ 1 c ⃗ 0 ⃗ \vec{c}\lambda\vec{…
阅读更多...
【白皮书下载】分布式功能安全的创新与突破

【白皮书下载】分布式功能安全的创新与突破

近日&#xff0c;Imagination 推出全新性能最高且具有高等级功能安全性的汽车 GPU IP——Imagination DXS GPU&#xff0c;并且是Imagination 第一款带有“分布式安全机制”的处理器。 下载白皮书&#xff0c;获取完整分布式安全机制解决方案 根据 ISO 26262 汽车安全完整性等级…
阅读更多...
STL 源码剖析 | 第1章：概论

STL 源码剖析 | 第1章：概论

STL 是一套程序库 1、STL 概论 1、从子程序、程序、函数、类别&#xff0c;到函数库、类别库、各种组件&#xff0c;从结构化设计、模块化设计、面向对象设计&#xff0c;到模式的归纳整理 为的就是 复用性 的提升 复用性 必须建立在某种标准之上 —— 不论是 语言层次的标…
阅读更多...
关于MATLAB计算3维图的向量夹角总是不正确的问题记录

关于MATLAB计算3维图的向量夹角总是不正确的问题记录

文章目录 问题描述解决方法完整代码 问题描述 因为最近在做无人机的一个项目&#xff0c;所以需要画出无人机的轨迹&#xff0c;然后再提取特征值&#xff0c;我这里在计算夹角的时候发现为什么在视觉上明明看的是钝角但是实际计算出来却是锐角的角度。 如下图所示&#xff0c…
阅读更多...
大觅网之环境部署（Environment Deployment of Da Mi Network）

大觅网之环境部署（Environment Deployment of Da Mi Network）

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:Linux运维老纪的首页…
阅读更多...
数据保护从现在开始：如何抵御 .[RestoreBackup@cock.li].SRC 勒索病毒

数据保护从现在开始：如何抵御 .[RestoreBackup@cock.li].SRC 勒索病毒

导言 勒索病毒是一种不断演变的网络威胁&#xff0c;.[RestoreBackupcock.li].SRC、[chewbaccacock.li].SRC勒索病毒便是其中一种新型的攻击手段。该病毒通过加密用户文件并要求支付赎金来恢复访问&#xff0c;给个人和企业带来了严重的安全风险和经济损失。本文91数据恢复将探…
阅读更多...
uniapp使用uview2上传图片功能

uniapp使用uview2上传图片功能

官网地址Upload 上传 | uView 2.0 - 全面兼容 nvue 的 uni-app 生态框架 - uni-app UI 框架 前提&#xff0c;需要下载vuew2插件 <view class"upload"><view class"u-demo-block__content"><view class"u-page__upload-item"&…
阅读更多...
进程状态的优先级

进程状态的优先级

1.进程的状态&#xff08;所有系统&#xff09; 因为是对于所有系统的&#xff0c;所以描述会很抽象。 补充知识&#xff1a; 并行和并发 并行&#xff1a;多个进程再多个cpu下分别同时运行并发&#xff1a;多个进程在一个cpu下采取进程切换的方式&#xff0c;在一段时间内&…
阅读更多...
fiddler抓包06_抓取https请求（chrome）

fiddler抓包06_抓取https请求（chrome）

课程大纲 首次安装Fiddler&#xff0c;抓https请求&#xff0c;除打开抓包功能&#xff08;F12&#xff09;还需要&#xff1a; ① Fiddler开启https抓包 ② Fiddler导出证书&#xff1b; ③ 浏览器导入证书。 否则&#xff0c;无法访问https网站&#xff08;如下图&#xff0…
阅读更多...
prometheus通过nginx-vts-exporter监控nginx

prometheus通过nginx-vts-exporter监控nginx

Prometheus监控nginx有两种方式。 一种是通过nginx-exporter监控&#xff0c;需要开启nginx_stub_status,主要是nginx自身的status信息&#xff0c;metrics数据相对较少&#xff1b; 另一种是使用nginx-vts-exporter监控&#xff0c;但是需要在编译nginx的时候添加nginx-module…
阅读更多...
MyBatis 分批次执行（新增，修改，删除）

MyBatis 分批次执行（新增，修改，删除）

import com.google.common.collect.Lists;import java.util.Iterator; import java.util.List; import java.util.function.Consumer;/*** Description mybatis分批插入数据使用* Author WangKun* Date 2024/9/19 11:20* Version*/ public class MyBatisSqlUtils {/*** param d…
阅读更多...
用户态缓存：高效数据交互与性能优化

用户态缓存：高效数据交互与性能优化

目录 1. 用户态缓存区工作背景 1.1 为什么每条连接都需要读写缓存区 1.1.1 读缓存区&#xff08;Read Buffer&#xff09; 1.1.2 写缓存区&#xff08;Write Buffer&#xff09; 1.2 用户态缓存区的工作流程 1.3 用户态缓存区的重要性 2. UDP 和 TCP 的设计差异 2.1 UD…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023