大家好,欢迎来到无限大的频道。
今日继续给大家带来力扣题解。
题目描述(困难):
统计特殊整数
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
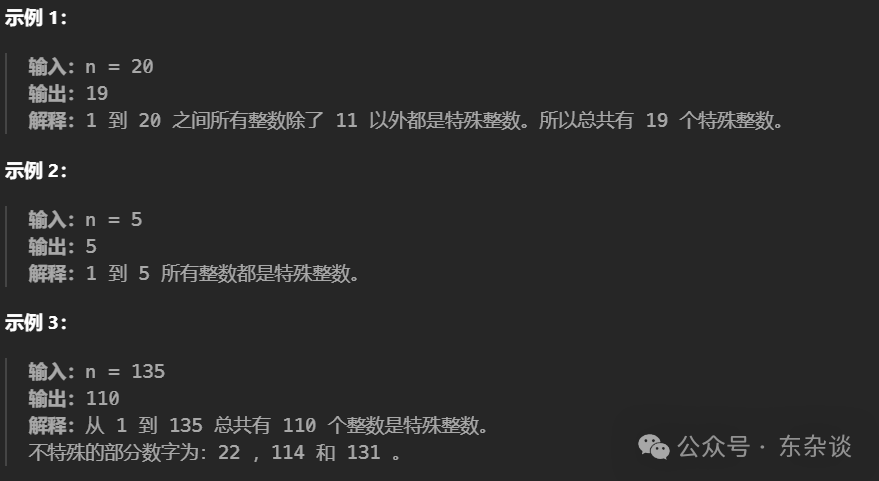
解题思路:
要计算区间 ([1, n]) 之间的特殊整数数量,可以按以下步骤进行:
-
定义特殊整数:
-
一个特殊整数是指其每一个数位都是互不相同的,即没有重复的数字。
-
-
遍历和检查:
-
遍历每一个整数从 1 到 n,检查每个整数是否为特殊整数。
-
对于每个整数,可以将其分解为其各个数字,并检查这些数字是否有重复。
-
-
利用集合判断重复:
-
可以通过一个数组或集合来记录某个数字是否已经出现。
-
-
计数特殊整数:
-
如果当前数字是特殊整数,将计数器加一。遍历结束后,输出计数器的值。
-
参考代码如下:
bool is_special_integer(int num) {
bool digit_seen[10] = {false}; // 标记每个数字是否出现过
while (num > 0) {
int digit = num % 10; // 取出当前的末尾数字
if (digit_seen[digit]) { // 如果该数字已经出现过
return false; // 不是特殊整数
}
digit_seen[digit] = true; // 标记该数字出现过
num /= 10; // 去掉当前数字
}
return true; // 所有数字都互不相同
}
int countSpecialNumbers(int n) {
int count = 0; // 特殊整数计数器
for (int i = 1; i <= n; i++) {
if (is_special_integer(i)) { // 判断是否为特殊整数
count++; // 增加计数
}
}
return count; // 返回特殊整数的数量
}代码解析:
-
is_special_integer 函数:
-
输入一个整数 num 并检查其每位数字是否互不相同。使用一个布尔数组 digit_seen 来记录 0-9 这 10 个数字的出现情况。
-
-
countSpecialNumbers 函数:
-
遍历 1 到 n 的所有整数,调用 is_special_integer 函数来判断该数字是否是特殊的,并更新计数器。
-
但是此代码的时间复杂度过高,测试用例超过了限定时间,所以要进行优化。
解题思路:
-
理解特殊整数:
-
特殊整数是在其每一位上没有重复的数字(例如,123、456是特殊整数,但 112、121、123 等不是)。
-
-
动态规划 + 记忆化搜索:
-
mask:用于表示当前已经使用的数字,采用位掩码。
-
prefixSmaller:表示当前构建的前缀数字是否小于目标数字的前缀。
-
nStr:将 ( n ) 转换成字符串形式,以便逐位处理各数字。
-
使用动态规划和哈希表来存储已经计算过的状态,以避免重复计算,提升效率。
-
状态定义:
-
-
递归函数 (DP):
-
通过递归函数 dp 实现动态规划,当当前使用的数字数量等于 ( n ) 的位数时返回 1。
-
对于每个数字,可以根据当前的状态,在允许的范围内选择下一个数字(既 [0,9] 中未被使用的数字)。
-
通过哈希表 memo 存储计算过的 mask 和 prefixSmaller 的组合,以加速后续计算。
-
-
计算统计:
-
首先计算位数小于 ( n ) 的所有特殊整数数量;
-
然后计算与 ( n ) 有相同位数的特殊整数数量。
-
参考代码如下:
typedef struct {
int key;
int val;
UT_hash_handle hh;
} HashItem;
HashItem *hashFindItem(HashItem **obj, int key) {
HashItem *pEntry = NULL;
HASH_FIND_INT(*obj, &key, pEntry);
return pEntry;
}
bool hashAddItem(HashItem **obj, int key, int val) {
if (hashFindItem(obj, key)) {
return false;
}
HashItem *pEntry = (HashItem *)malloc(sizeof(HashItem));
pEntry->key = key;
pEntry->val = val;
HASH_ADD_INT(*obj, key, pEntry);
return true;
}
bool hashSetItem(HashItem **obj, int key, int val) {
HashItem *pEntry = hashFindItem(obj, key);
if (!pEntry) {
hashAddItem(obj, key, val);
} else {
pEntry->val = val;
}
return true;
}
int hashGetItem(HashItem **obj, int key, int defaultVal) {
HashItem *pEntry = hashFindItem(obj, key);
if (!pEntry) {
return defaultVal;
}
return pEntry->val;
}
void hashFree(HashItem **obj) {
HashItem *curr = NULL, *tmp = NULL;
HASH_ITER(hh, *obj, curr, tmp) {
HASH_DEL(*obj, curr);
free(curr);
}
}
int dp(int mask, bool prefixSmaller, const char *nStr, HashItem **memo) {
if (__builtin_popcount(mask) == strlen(nStr)) {
return 1;
}
int key = mask * 2 + (prefixSmaller ? 1 : 0);
if (!hashFindItem(memo, key)) {
int res = 0;
int lowerBound = mask == 0 ? 1 : 0;
int upperBound = prefixSmaller ? 9 : nStr[__builtin_popcount(mask)] - '0';
for (int i = lowerBound; i <= upperBound; i++) {
if (((mask >> i) & 1) == 0) {
res += dp(mask | (1 << i), prefixSmaller || i < upperBound, nStr, memo);
}
}
hashAddItem(memo, key, res);
}
return hashGetItem(memo, key, 0);
}
int countSpecialNumbers(int n) {
char nStr[64];
sprintf(nStr, "%d", n);
int res = 0;
int prod = 9;
int len = strlen(nStr);
HashItem *memo = NULL;
for (int i = 0; i < len - 1; i++) {
res += prod;
prod *= 9 - i;
}
res += dp(0, false, nStr, &memo);
hashFree(&memo);
return res;
}代码分析:
1. 哈希表结构与操作
typedef struct {
int key;
int val;
UT_hash_handle hh; // 哈希表的内部处理
} HashItem; -
定义了一个结构体 HashItem,用于存储键值对(key 和 val),并使用 UT_hash_handle 宏,以便利用 uthash 提供的哈希表功能。
-
哈希表相关操作如下:
HashItem *hashFindItem(HashItem **obj, int key);
bool hashAddItem(HashItem **obj, int key, int val);
bool hashSetItem(HashItem **obj, int key, int val);
int hashGetItem(HashItem **obj, int key, int defaultVal);
void hashFree(HashItem **obj);-
hashFindItem 查找哈希表的项。
-
hashAddItem 添加项到哈希表,如果已存在则返回 false。
-
hashSetItem 设置某项的值,如果不存在,则插入新项。
-
hashGetItem 获取项的值,若不存在则返回默认值。
-
hashFree 释放哈希表的内存。
2. 动态规划函数 dp
int dp(int mask, bool prefixSmaller, const char *nStr, HashItem **memo) {
// 检查当前使用的数字数量是否等于目标字符串的数量
if (__builtin_popcount(mask) == strlen(nStr)) {
return 1; // 如果是,返回 1,表示成功构造了一个有效的特殊整数
}
// 生成一个唯一的键以访问缓存
int key = mask * 2 + (prefixSmaller ? 1 : 0);
// 如果当前状态没有被计算过
if (!hashFindItem(memo, key)) {
int res = 0;
int lowerBound = (mask == 0) ? 1 : 0; // 第一个数字不能是 0
// 确定当前可以选择的数字上限
int upperBound = prefixSmaller ? 9 : nStr[__builtin_popcount(mask)] - '0';
// 尝试选择每一个数字
for (int i = lowerBound; i <= upperBound; i++) {
if (((mask >> i) & 1) == 0) { // 检查当前数字是否未被使用
// 递归调用,加入当前选择并更新状态
res += dp(mask | (1 << i), prefixSmaller || (i < upperBound), nStr, memo);
}
}
hashAddItem(memo, key, res); // 缓存当前状态的结果
}
return hashGetItem(memo, key, 0); // 返回缓存的结果或 0
}-
dp 函数中,使用 mask 来表示当前使用的数字,利用位运算避免重复。
-
使用 prefixSmaller 判断当前构造的数字是否小于对应的 ( n ) 的前缀。
-
计算当前状态下所能构造的特殊整数数量,并将其缓存到哈希表中。
3. 主函数 countSpecialNumbers
int countSpecialNumbers(int n) {
char nStr[64];
sprintf(nStr, "%d", n); // 将 n 转换为字符串形式
int res = 0;
int prod = 9; // 可能的数字引导初始值为 9
int len = strlen(nStr); // 目标长度
HashItem *memo = NULL; // 初始化缓存
// 计算所有位数小于 n 的特殊整数的数量
for (int i = 0; i < len - 1; i++) {
res += prod; // 将当前的数量加入结果
prod *= 9 - i; // 更新可能的选择数
}
res += dp(0, false, nStr, &memo); // 计算与 nStr 长度相同的特殊整数
hashFree(&memo); // 释放内存
return res; // 返回总结果
}-
主函数中,首先将 ( n ) 转为字符串以便逐位处理。
-
计算所有位数小于 ( n ) 的特殊整数数量。
-
通过 dp 函数计算与 ( n ) 有相同位数的特殊整数数量。
-
最后释放内存并返回结果。
总结:
整段代码结合了动态规划与哈希表的缓存机制,优雅地解决了问题:
-
通过位掩码有效记录已使用的数字。
-
通过记忆化搜索加速计算,避免重复递归。
-
提供了高效的方式来计算区间 ([1, n]) 中所有特殊整数的数量,可以适用于较大的数字范围。
这种方法的时间复杂度主要由位数 ( m ) 影响,且结合了组合的计算,通常在实际问题中能够高效运行。



















