74、Python之函数式编程：深入理解惰性求值与生成器

news2024/11/12 19:14:18

引言

我们在过程式编程或者面向对象编程中（当然也不局限于这些），涉及到计算、数据的转换处理时，通常是执行到对应的语句或者表达式时，就会完成计算或者数据处理。大多数场景下，这样立即计算的方式是没有问题的，但是当涉及到大数据场景时，可能会存在性能上的问题。

本文介绍的函数式编程中的另一个关键特性：惰性求值，可以用来涉及到大数据的计算、处理场景。

本文的主要内容有：

1、什么是惰性求值

2、惰性求值的适用场景

3、基于生成器实现惰性求值

什么是惰性求值

所谓“惰性求值（Lazy Evaluation）”是一种计算的策略，即在真正需要时才进行计算，而不是立即计算。

在惰性求值中，表达式的计算被推迟，直到结果确实需要的时候才进行真正的计算。

与之相对的是“及早计算（Eager Evaluation）”，这种策略是我们之前已经广泛使用到的，执行到表达式时，就会立即完成计算，并获取结果。

在不同的教材中，有时也会用另一种表述方式：“严格求值”与“非严格求值”。从字面意思就可以理解，所谓严格求值就是及早计算，所谓非严格求值就是惰性求值的意思。

需要说明的是，前面的其他特性更多的体现了函数式编程范式的简洁性、状态管理比较清晰、易于调试、测试等。而函数式编程之所以高效，原因之一就在于这种惰性求值的特性。

其实，Python或者其他语言中，经常用到的“短路运算”，也可以算作是惰性求值的一种形式。

比如：

age = 19
age >= 18 and print('成年人可以进网吧')
print('=' * 20)
age = 12
# 短路，后两行的print()均不会执行
age >= 18 and print('成年人可以进网吧')
age < 18 or print('未成年人等几年再来吧，如果网吧还在的话')

上面代码中，只有第一个print()会被执行，最后两个print()都不会被执行，由于短路运算的操作，没有执行的必要了。

在Python中，运算符and、or和if-else等都是非严格的，因为它们不需要计算全部参数就能提前得到整个表达式的最终结果了。

在其他语言中，也有同样的短路运算的实现。

惰性求值的适用场景

惰性求值的出发点在于进行性能优化，提升效率。所以，只要涉及到有性能优化的需要，都可以试着考虑能否通过惰性求值来实现。

惰性求值的典型场景主要有：

1、处理大数据集：当需要处理无法一次性装入内存的大数据集时，比如较大的文件、大型数据库的查询结果等，都可以使用惰性求值来优化内存的使用。

2、生成无限序列：如果需要一个无限的序列或者序列比较大，很可能导致内存溢出，这时，也可以考虑使用惰性求值来实现。

3、延迟计算以提高性能：当某些计算开销较大时，但是，并不总是需要用到其计算结果，那么就可以使用惰性求值，从而避免不必要的计算，从而提高性能。

4、流处理（Stream Processing）：在大数据计算中，除了离线的批量计算外，还有一类场景的使用越来越频繁，就是实时大数据处理，也可以理解为实时流式数据处理，数据像流水一样，是持续的流转的，比如用户行为日志、传感器的监测数据等。这些场景也适合惰性求值。

基于生成器实现惰性求值

在Python中，要实现惰性求值，除了前面提到的“短路运算”外，其实更常用的是使用“生成器”。

生成器（Generator）是Python中一种特殊的迭代器，允许我们以惰性（lazy）的方式来生成序列的元素。

生成器主要是使用yield关键字来返回值，而不是像普通函数那样使用return返回。生成器函数在每次被调用时会暂停，并在下次调用时继续执行当前的位置，从而节省内存和提高效率。

Python中有两种方式来使用生成器：

1、使用生成器表达式来获得生成器，类似于列表推导式，只需要把[]换为()，既可以快速得到一个生成器。

2、通过定义函数的方式定义一个生成器，主要是使用yield关键字。

生成器表达式

首先来看生成器表达式的使用，直接看代码：

nums_list = [x * x for x in range(10)]
nums_generator = (x * x for x in range(10))
print(type(nums_list))
print(nums_list)
print('=' * 20)
print(type(nums_generator))
print(nums_generator)
print(list(nums_generator))
# 生成器可以使用for进行遍历
for num in nums_generator:
    print(num, end=' ')

执行结果：

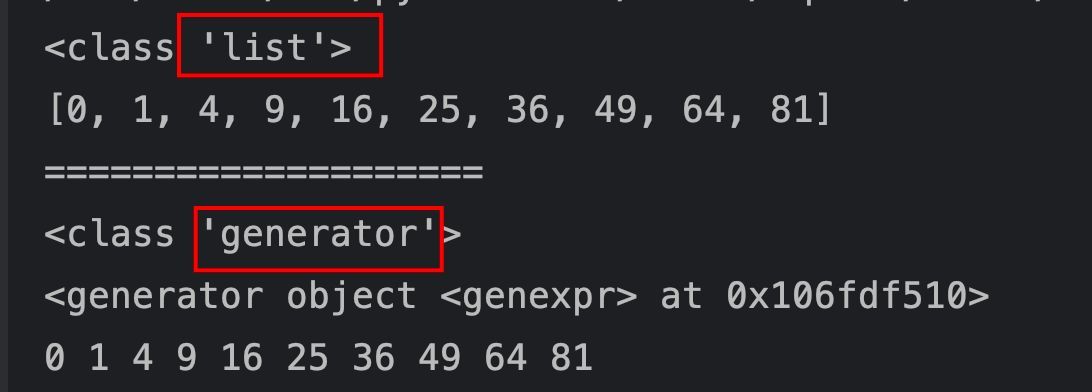
从上述程序的执行可以得出：

1、列表推导式得到的是一个真实的列表对象，会直接占用对应的内存。

2、生成器表达式得到的是一个生成器对象，并不会直接分配同样大小的内存，只有在对生成器进行遍历时，才会真正计算每一个需要的元素。

3、两者在定义语法上的区别，只有[]与()的区别。

需要说明的是，列表可以进行多次遍历，但是，生成器只能进行一次遍历，所有的元素遍历完成了，不会从头来过。

此外，可以使用list(生成器对象)的方式将生成器对象转换为一个列表对象，本质上是对生成器对象进行遍历，用获得到的所有元素构建一个新的列表对象。当然构建之后，生成器对象本身如果使用for进行遍历，是获取不到任何元素的，因为已经被遍历一趟了。小数据集时，可以进行这种操作，数据量比较大时，需要注意性能。

使用yield定义生成器

直接看一个定义生成器函数的代码实例：

# 定义生成器函数
def square_num():
    for i in range(10):
        print(f'开始遍历，此时i={i}')
        yield i * i
        print(f'一次遍历完成')


print(type(square_num))
# 当进行函数调用时，则会获得生成器对象
generator = square_num()
print(type(generator))
print('=' * 20)
print(generator.__next__())
print('=' * 20)
print(next(generator))
print('=' * 30)
for num in generator:
    print(num)

执行结果：比较多，没有截全图

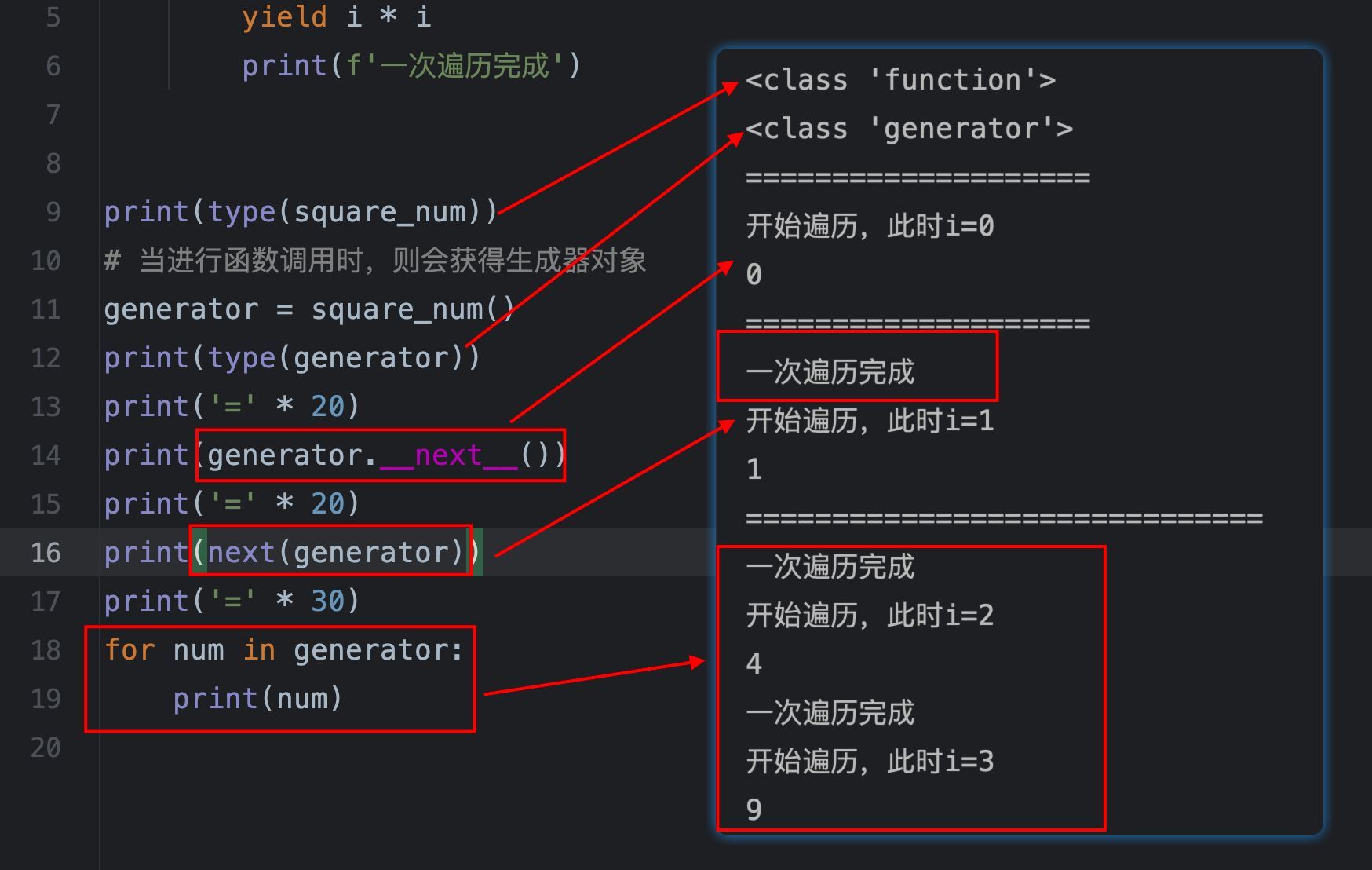
从这个生成器函数的定义及执行，可以得到如下结论：

1、在函数中使用了yield关键字，则该函数自动变为生成器函数，进行函数调用时，会获得一个生成器对象。

2、生成器对象是惰性求值的，每次手动调用next(生成器对象)或者调用生成器对象.__next__()方法，可以进行一次求值计算，返回内容为yield表达式后面的值。

3、每次求值计算，执行到yield表达式，就会阻塞，同时返回对应的值。下一次求值计算，从上次的阻塞点开始，继续执行。所以，能看到“一次遍历完成”出现在下一次求值计算的开头，而不是上一次求值计算的结尾。

此外，虽然代码演示中，没有涉及到，但是，还是有两点需要补充的：

1、生成器其实是一种特殊的迭代器，从定义中可以看到，生成器继承自迭代器：

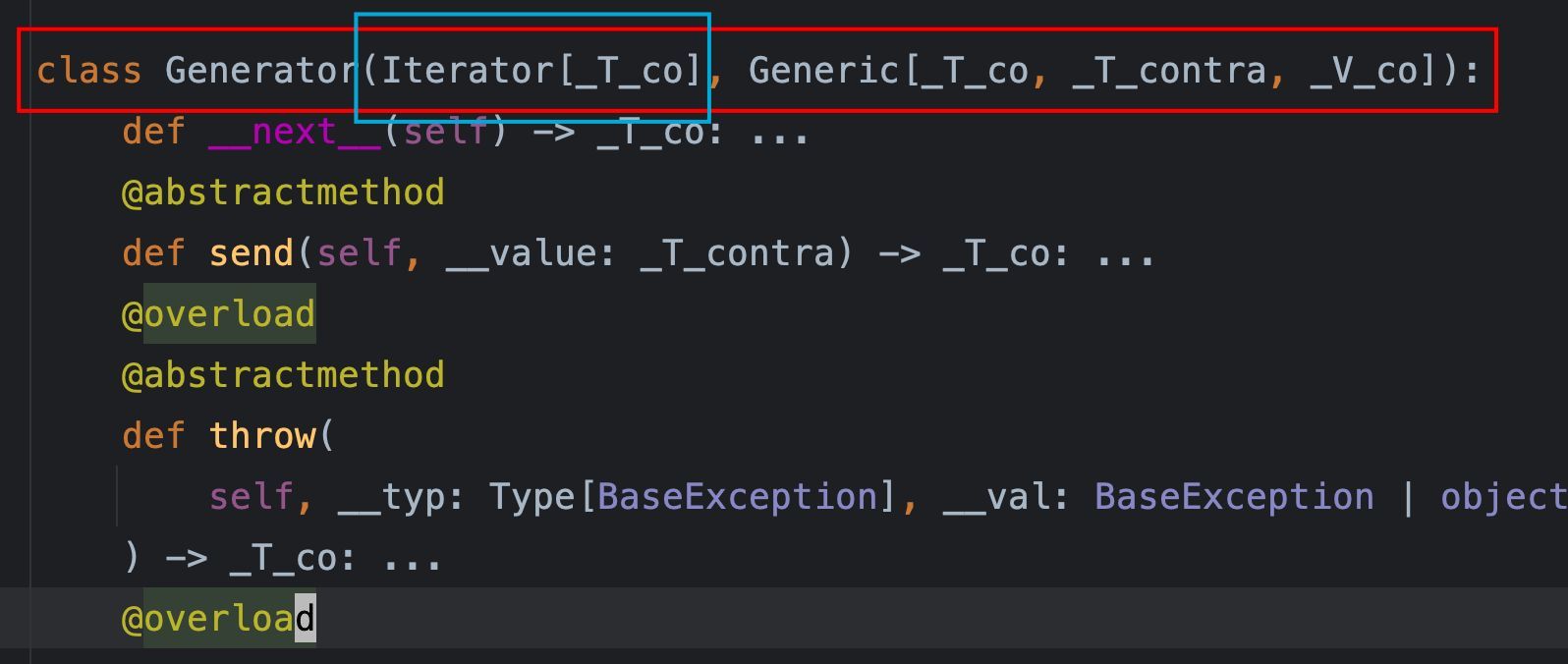
2、当一个生成器已经完成所有元素的遍历时，继续手动进行next()函数的调用，则会抛出“StopIteration”异常。使用for循环进行遍历则不会抛异常。

前面的文章中，我们已经通过多种方式进行斐波那契数列的计算了，比如自定义装饰器缓存、内置装饰器、一行流等。接下来，我们以生成器的方式来实现斐波那契数列的计算。

直接看代码：

# 定义斐波那契生成器函数
def fibonacci():
    a, b = 0, 1
    while True:
        yield a
        a, b = b, a + b


fib = fibonacci()
print(type(fib))
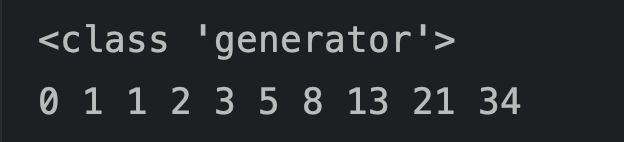
for i in range(10):
    print(next(fib), end=' ')

执行结果：