数据结构入门学习（全是干货）——树（中）

1 二叉搜索树（Binary Search Tree，简称 BST）

1.1 二叉搜索树及查找

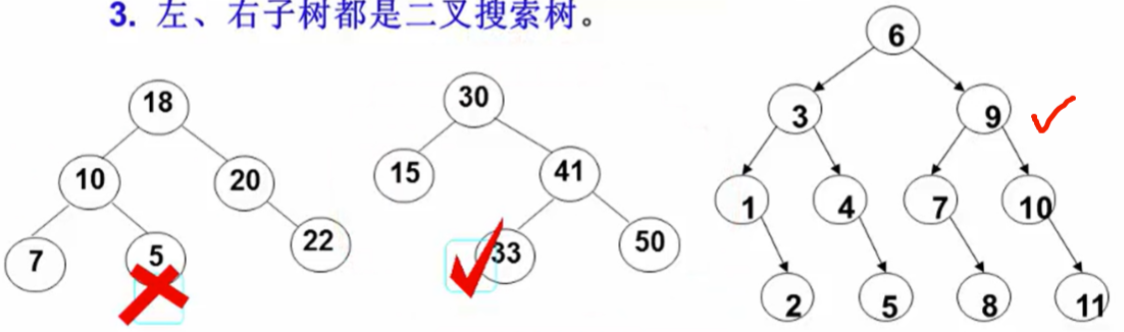
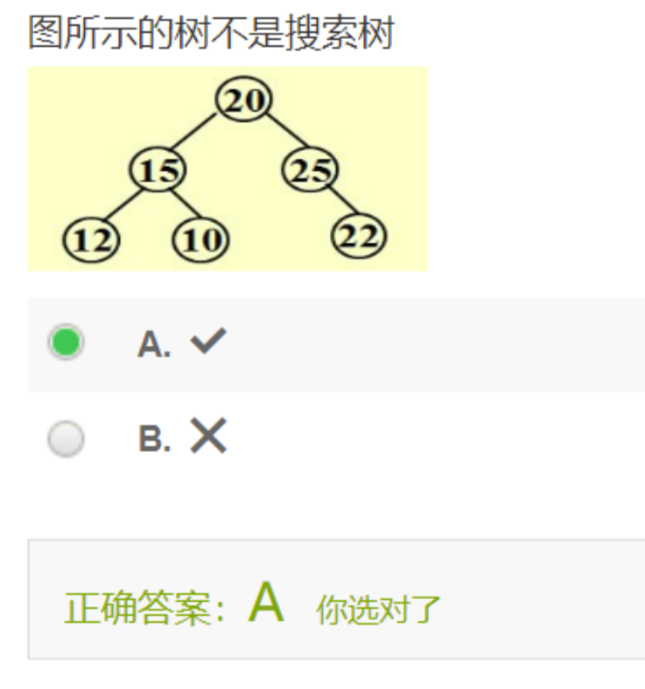
二叉搜索树（Binary Search Tree, BST） 是一种特殊的二叉树，它满足以下性质：

• 对于每一个节点，其左子树上所有节点的值都小于该节点的值。
• 右子树上所有节点的值都大于该节点的值。
• 每棵子树也是一棵二叉搜索树。

二叉搜索树的基本操作：

1. 查找元素（Find）

   查找从根结点开始，如果树为空，返回NULL
   
   若搜索树非空，则根结点关键字和X进行比较，并进行不同处理：
   	1.若X小于根结点赋值，只需在左子树中继续搜索;
   	2.如果X大于根结点的键值，在右子树中进行继续搜索;
   	3.若两者比较结果是相等，搜索完成，返回指向此结点的指针
   

   Position Find(ElementType X,BinTree BST)
   {
   	if(!BST) return NULL;//查找失败
       if( X > BST -> Data)//这是尾递归，下面的两个Find的也是同理
           return Find(X,BST->Right);//在右子树中继续查找
       Else if(X < BST -> Data)
           return Find(X,BST->Left);//在左子树中继续查找
       else//X == BST->Data
           return BST;//查找成功，返回结点的找到结点的地址
   }
   
   
   //由于非递归函数的执行效率高，可将"尾递归"函数改为迭代函数
   Position IterFind(ElementType X,BinTree BST)
   {
   	while(BST){
           if(X > BST->Data)
               BST = BST -> Right;//向右子树中移动，继续查找
           else if(X < BST->Data)
               BST = BST ->Left;//向左子树中移动，继续查找
           else//X == BST ->Data
               return BST;//查找成功，返回结点的找到结点的地址
       }
           return NULL;//查找失败
   }
   
   //查找的效率决定于树的高度
   

2. 插入元素

3. 删除元素

查找最大和最小元素

• 查找最小元素：从根节点开始，沿左子树一直往下找到最左端的叶子节点。
• 查找最大元素：从根节点开始，沿右子树一直往下找到最右端的叶子节点。

查找最小元素的递归函数示例：

Node* findMin(Node* root) {
    if (root == nullptr || root->left == nullptr)
        return root;
    return findMin(root->left);
}

查找最大元素的迭代函数示例：

Node* findMax(Node* root) {
    while (root->right != nullptr)
        root = root->right;
    return root;
}

1.2 二叉搜索树的插入

插入操作的关键是要找到元素应该插入的位置，这与查找操作类似。插入时，我们从根节点开始，与节点的值进行比较：

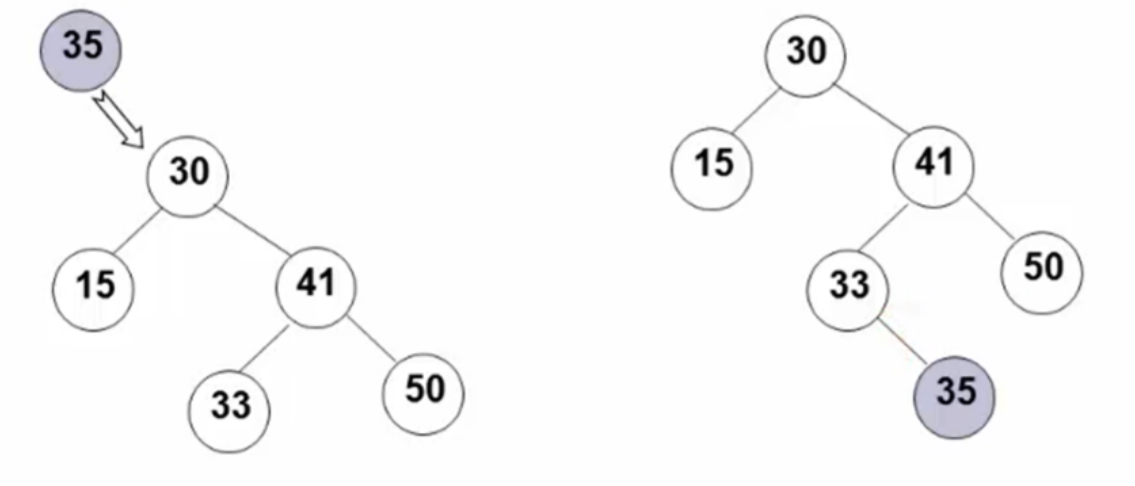
• 如果插入的值小于当前节点的值，则递归到左子树。
• 如果插入的值大于当前节点的值，则递归到右子树。
• 如果找到了空节点，则插入该元素。

插入元素的算法：

BinTree Insert(ElementType X,BinTree BST)
{
	if(!BST){
        //若原树为空，生成并返回一个结点的二叉搜索树
        BST = malloc(sizeof(struct TreeNode));
        BST -> Data = X;
        BST -> Left = BST -> Right = NULL;
    }else //开始找要插入元素的位置
        if(X < BST->Data )
            BST -> Left = Insert(X,BST->Left);//递归插入左子树
    else if(X > BST->Data)
        BST->Right = Insert(X,BST->Right);//递归插入右子树
    //else X已经存在，什么都不做
    return BST;
}

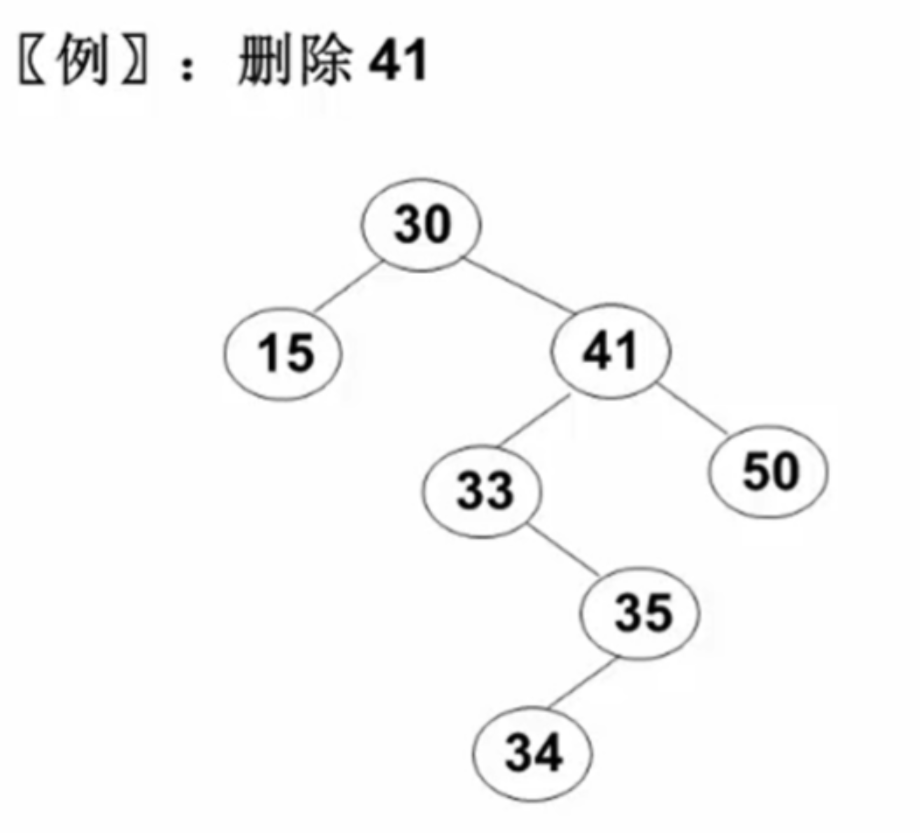
1.3 二叉搜索树的删除

删除一个节点需要考虑三种情况：

1. 删除的是叶结点：直接删除，并修改其父节点的指针为 NULL。

2. 删除的节点只有一个子节点：

   • 将其父节点的指针指向要删除节点的唯一孩子。

   

   

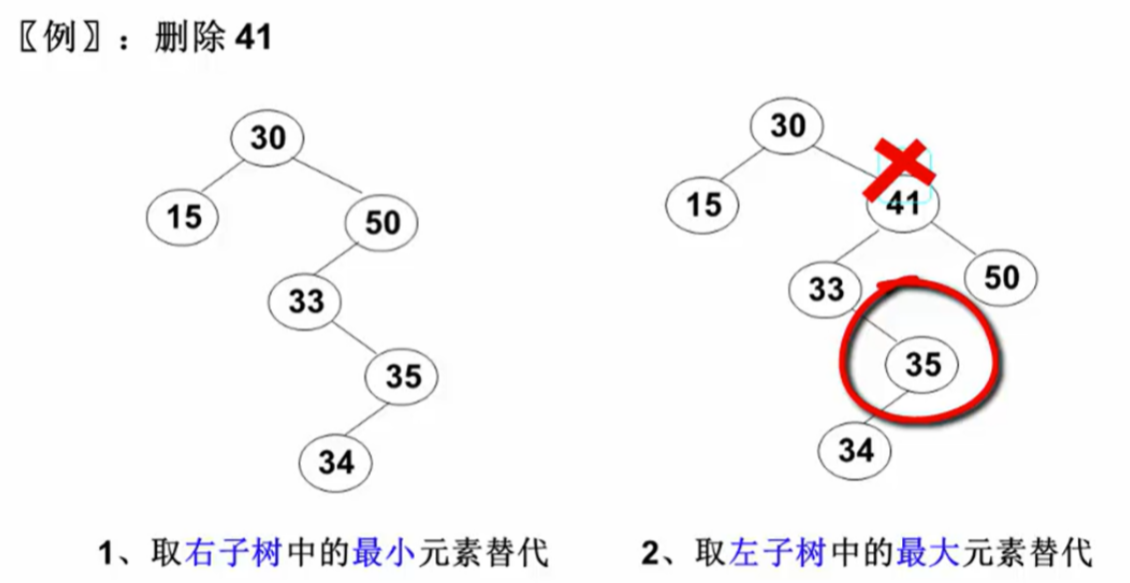
3. 删除的节点有两个子节点：

   • 用右子树的最小元素或左子树的最大元素替代被删除的节点，然后删除这个替代节点。

   

删除元素的代码实现：

BinTree Delete (ElementType X,BinTree BST)
{
	Position Tmp;   
    if(!BST) printf("要删除的元素未找到");
    else if(X < BST ->Data)
        BST->Left = Delete(X,BST->Left);//左子树递归删除,返回左子树删除了x这个结点之后，新的左子树根结点的地址
    else if(X > BST->Data)
        BST->Right = Delete( X,BST->Right);//右子树递归删除
    else//找到要删除的结点
        if(BST->Left && BST->Right ){//被删除结点有左右两个子节点
            Tmp = FindMin(BST->Right);//在右子树中找最小的元素填充删除结点
            BST->Data = Tmp->Data;
            BST->Right = Delete(BST->Data,BST->Right);//在删除结点的右子树中删除最小元素
        }else{//被删除结点有一个或无子结点
            Tmp = BST;
            if(!BST->Left)//有右孩子或无子结点
                BST = BST->Right;
            else if(!BST->Left)//有左孩子或无子结点
            	BST = BST->Left;
            free(Tmp);
        }
}
return BST;

---

2 平衡二叉树（Balanced Binary Tree）

2.1 什么是平衡二叉树

平衡二叉树是一种特殊的二叉树，其左子树和右子树的高度差不超过1（即左右子树的高度差最多为1）。如果一棵树的每个子树也都满足这个条件，则该树为平衡二叉树。

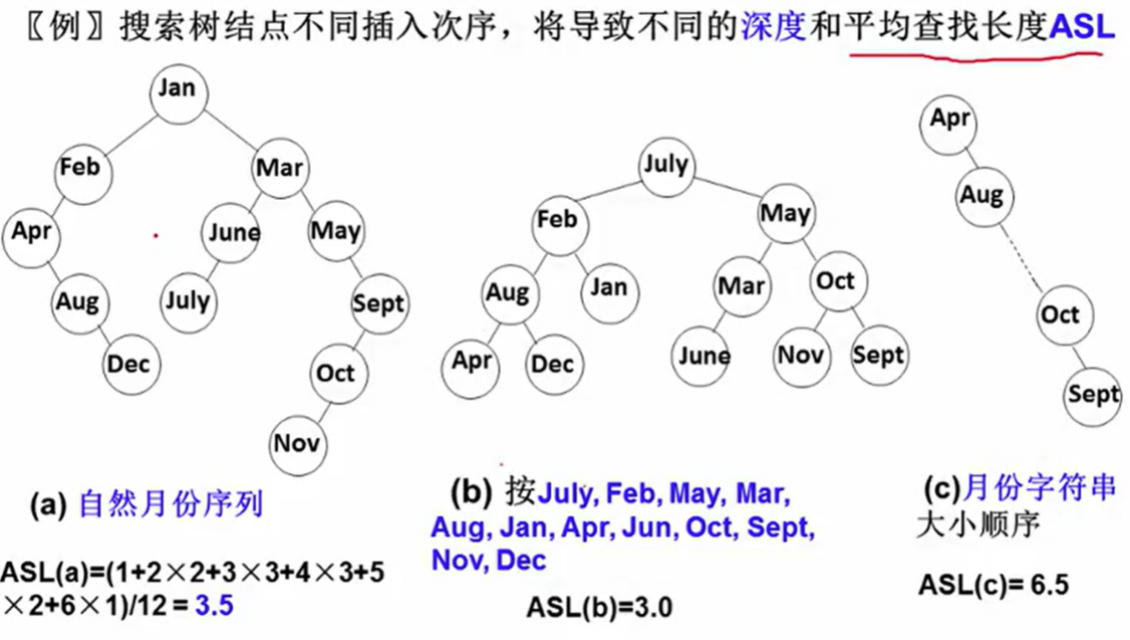
平衡因子：

平衡因子是某个节点左右子树的高度差。平衡因子计算公式：

平衡因子 = 左子树高度 - 右子树高度

对于平衡二叉树，所有节点的平衡因子绝对值都小于或等于1。

举例：

至少需要 7 个结点才能构造出一棵高度为 3 的平衡二叉树。

---

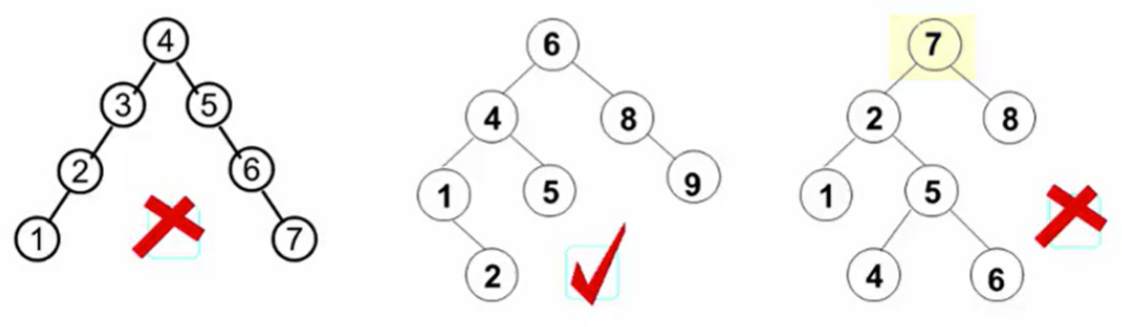
2.2 平衡二叉树的调整

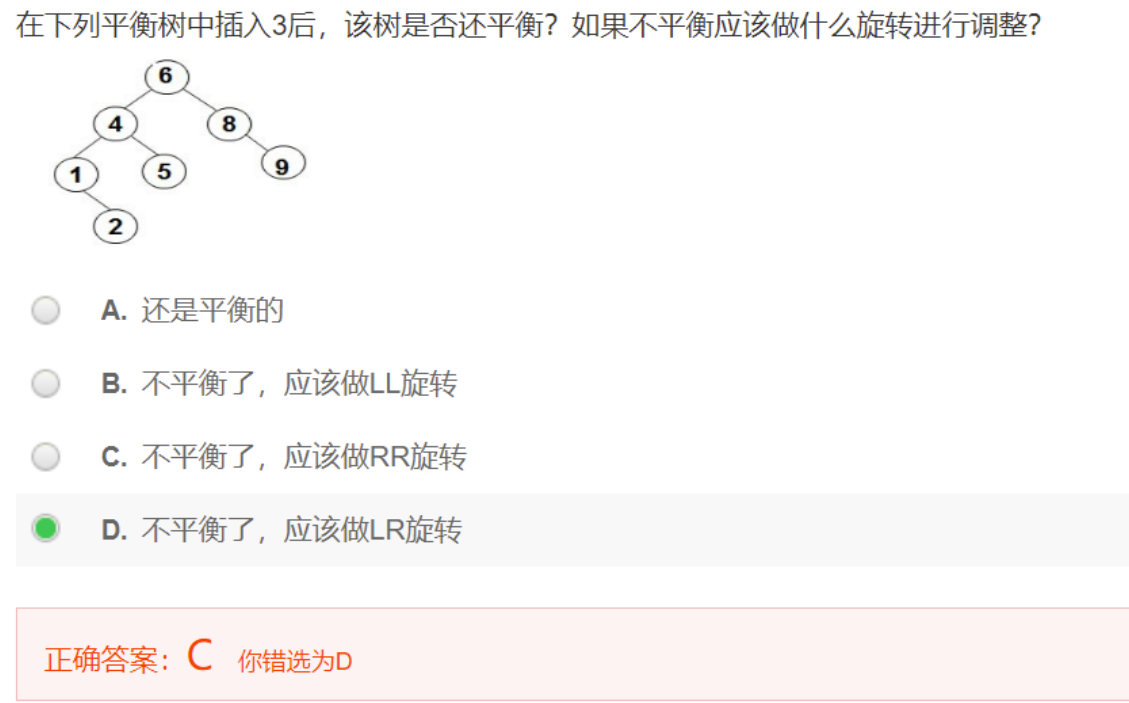
在二叉搜索树的插入或删除操作中，如果树的平衡被打破，就需要进行调整，使其重新成为平衡二叉树。调整的方法是旋转，常见的四种旋转操作有：

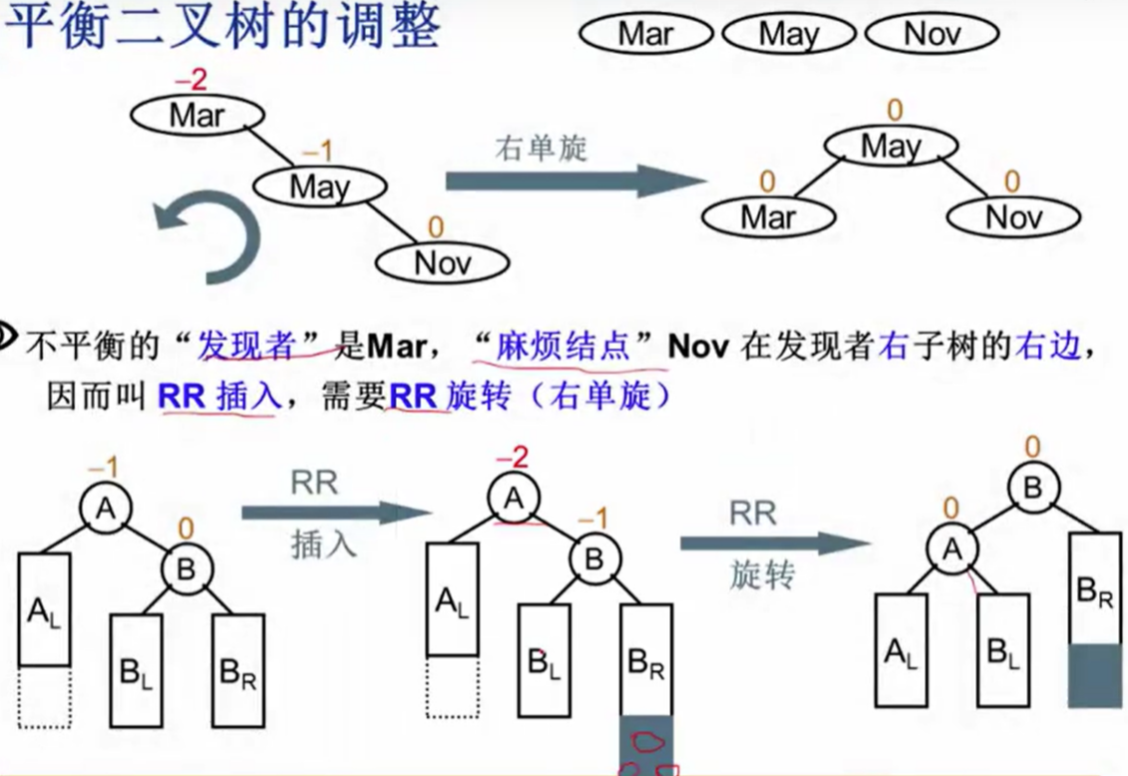
1. RR旋转（右右旋转）：

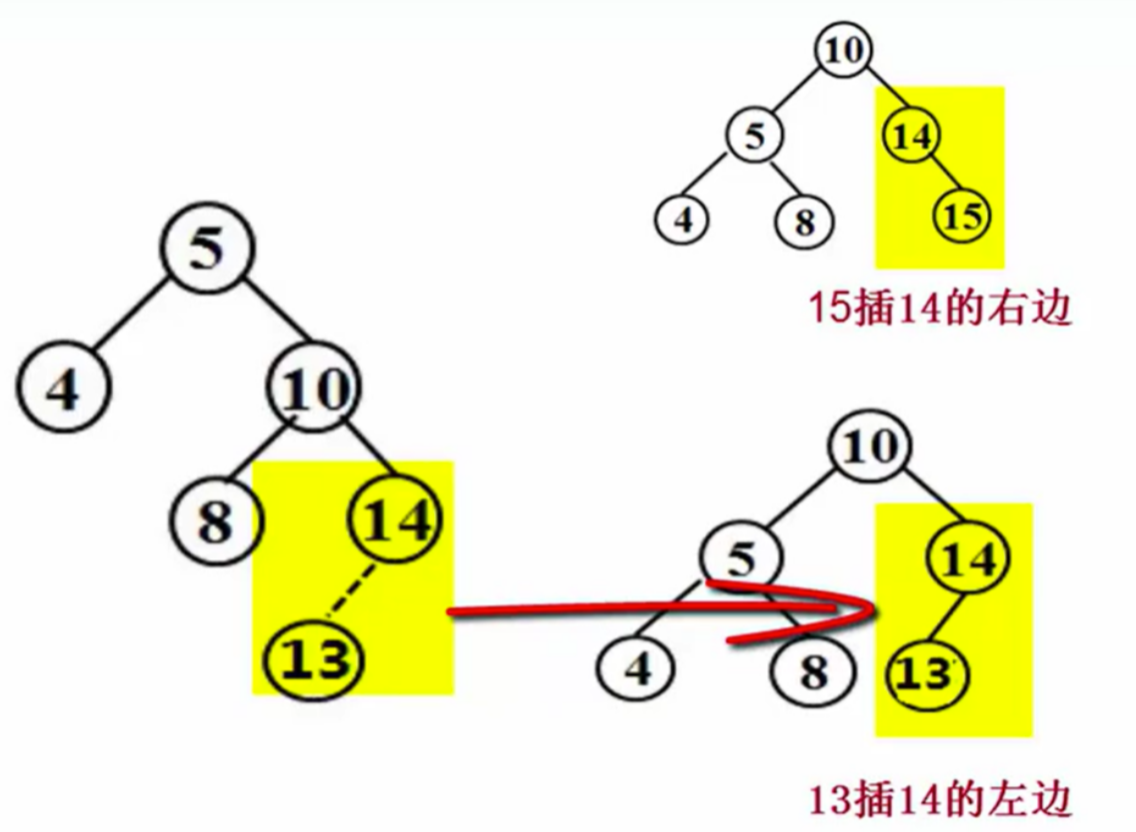
当插入点位于节点的右子树的右子树时，执行RR旋转。通过一次左旋，使树重新平衡。

2. LL旋转（左左旋转）：

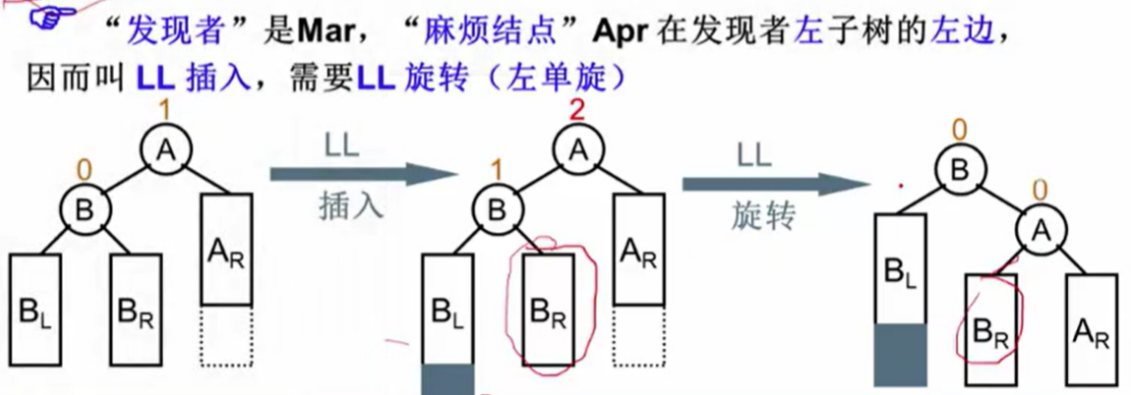
当插入点位于节点的左子树的左子树时，执行LL旋转。通过一次右旋，使树重新平衡。

3. LR旋转（左右旋转）：

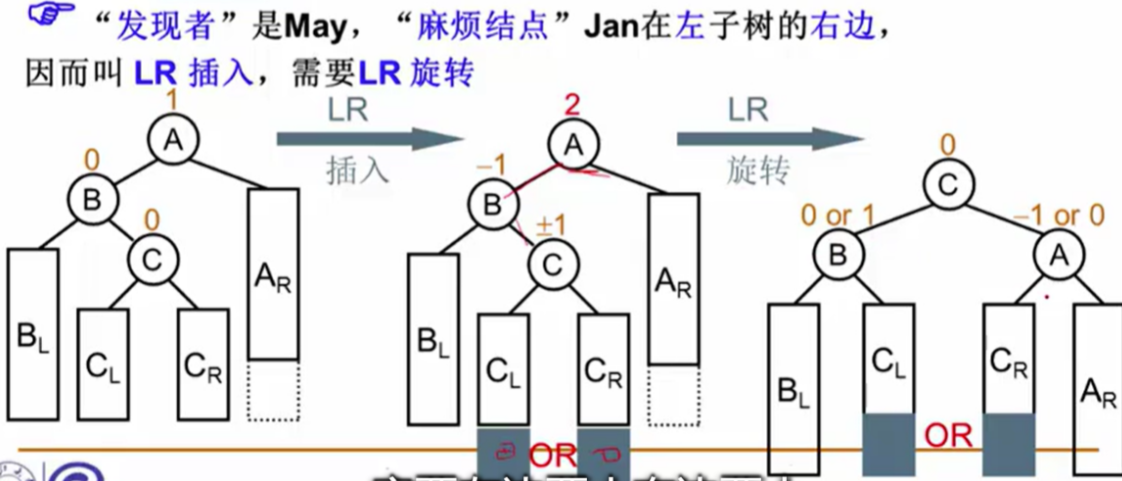
当插入点位于节点的左子树的右子树时，执行LR旋转。首先对左子树进行RR旋转，然后对整个树进行LL旋转。

4. RL旋转（右左旋转）：

当插入点位于节点的右子树的左子树时，执行RL旋转。首先对右子树进行LL旋转，然后对整个树进行RR旋转。

---

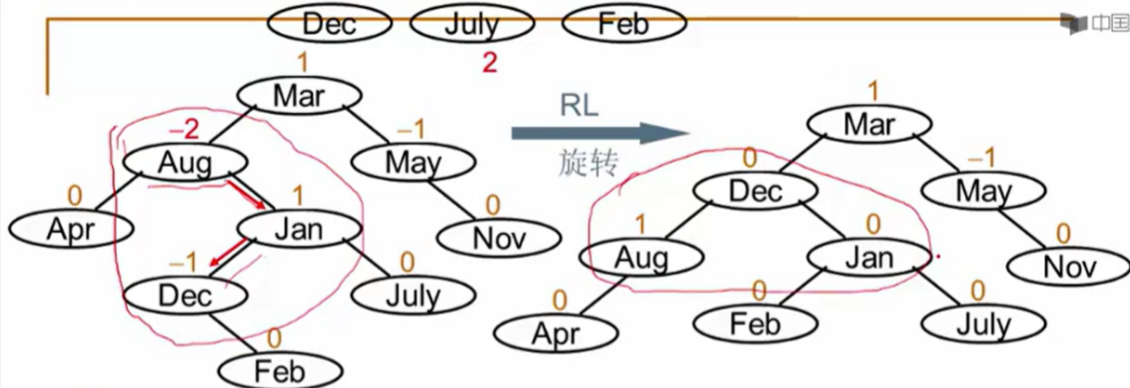
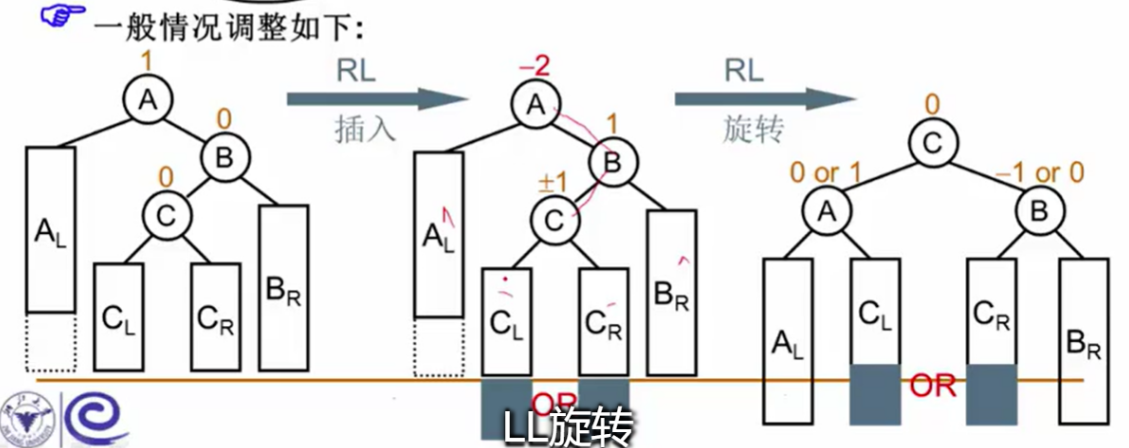
3 链表逆转

3.1 链表基本概念

链表是一种线性数据结构，每个节点包含两部分：

1. 数据域：存储数据。
2. 指针域：存储指向下一个节点的指针。

3.2 单链表逆转算法

链表逆转的核心思想是逐个反转节点的指针方向，以下是链表逆转的伪代码实现：

Ptr Reverse(Ptr head) {
    Ptr newHead = nullptr;
    Ptr oldHead = head;
    while (oldHead != nullptr) {
        Ptr temp = oldHead->next;
        oldHead->next = newHead;
        newHead = oldHead;
        oldHead = temp;
    }
    return newHead;
}

边界测试：

1. 链表长度为 0 或 1 的情况。
2. 链表长度恰好为反转单位长度的整数倍。
3. 逆转链表的其他边界情况。