近期,斯隆奖得主马腾宇和Google Brain推理团队创始人Denny Zhou合作,提出了一项引人注目的数学证明:只要思维链(CoT)足够长,Transformer就有能力解决各种复杂问题。这一发现引发了广泛关注,因为它为Transformer模型在推理算力方面的Scaling Law揭示了巨大的潜能

他们通过严谨的数学方法证明,Transformer具备模拟任意多项式大小数字电路的能力。这一研究成果也成功入选ICLR 2024。

正如一些网友所说,CoT的集成缩小了Transformer与图灵机之间的差距,为其实现图灵完备性铺平了道路。

这意味着,神经网络理论上可以高效解决复杂问题。简而言之:Compute is all you need!

思维链(CoT)让Transformer更强大
首先,需要明确的是,“可以解决任何问题”是一个通俗化的说法。严格来说,论文的核心结论是,思维链(CoT)能够显著提升Transformer的表达能力。
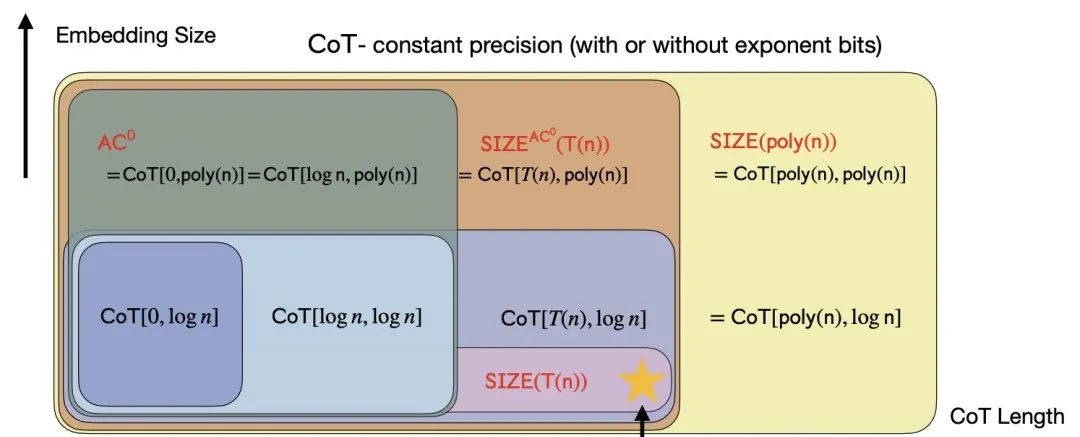
作者首先通过理论分析指出,对于固定深度、多项式宽度、常数精度的Transformer模型,如果不使用CoT,其表达能力将受限于AC0问题类别。(AC0是一类可以在并行计算中高效解决的问题,但不包括需要复杂序列化计算的问题。)
在固定指数位的情况下,即使引入了舍入操作,固定深度、对数精度的Transformer模型也只能处理TC0问题类别。
然而,一旦引入CoT,固定深度、常数精度的Transformer模型就可以解决任何由大小为T的布尔电路所解决的问题。
这表明CoT显著扩展了模型的表达能力,使其能够处理更复杂的问题。
实验验证:四个核心问题
为了验证理论分析,论文在四个核心问题上进行了实验,考虑了基础(base)、CoT和提示(hint)三种不同的训练设置:
-
模运算(Modular Addition):并行计算问题,验证CoT在提升模型准确性方面的效果;
-
置换群组合(Permutation Composition):序列化计算问题,验证CoT在处理这类任务上的有效性;
-
迭代平方(Iterated Squaring):典型的序列化计算问题,展示CoT如何使模型有效求解;
-
电路值问题(Circuit Value Problem):一个P完全问题,验证CoT在模型深度较低时的有效性。
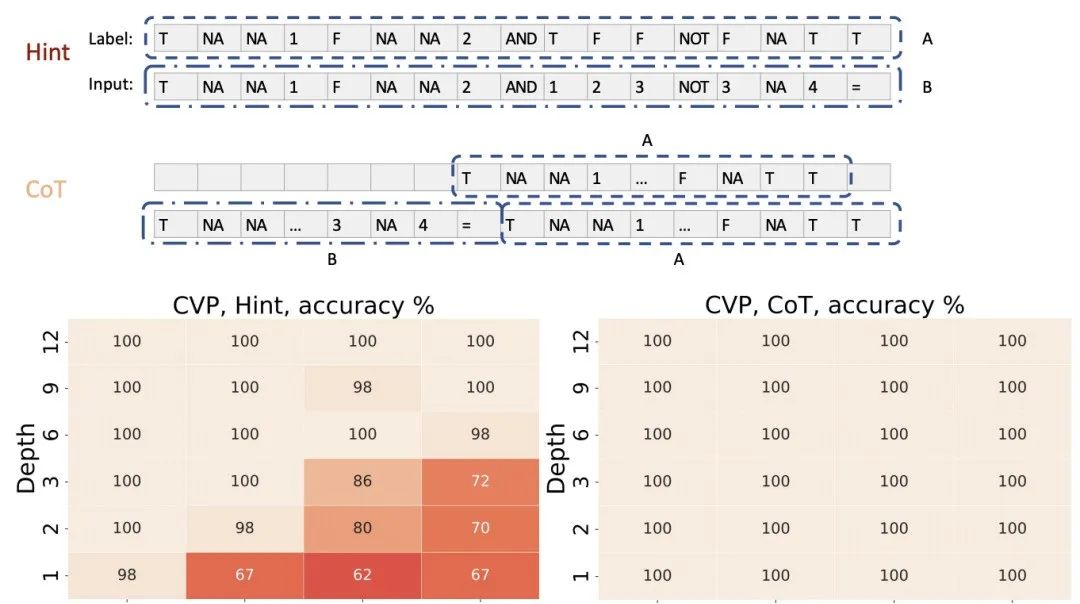
在模运算问题上,实验结果表明,所有设置下的Transformer都能学习模加;但在较长序列(如n=16)上,CoT展现出明显优势。这说明即使是并行问题,CoT也能提升效率。
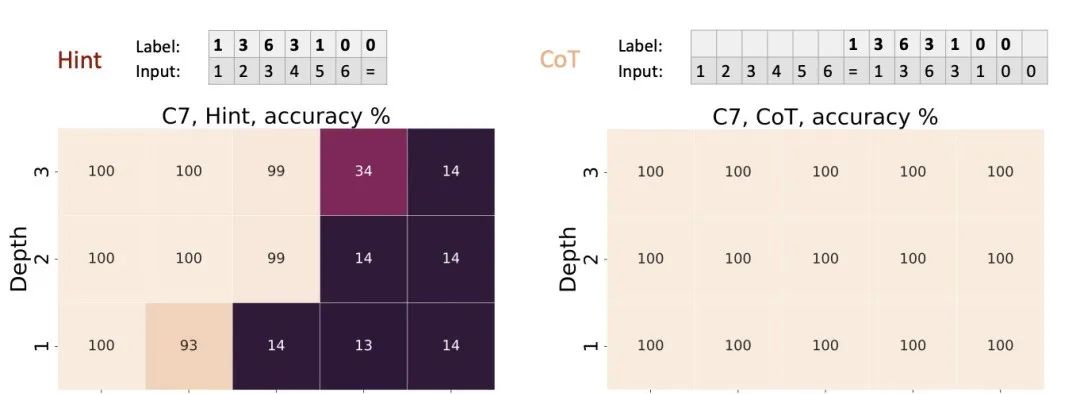
在置换群复合任务中,输入是S_5置换群中的若干个置换,输出是它们的复合结果。结果显示,CoT显著提高了低深度模型的准确性。未使用CoT的Transformer即使深度较大,准确率也只有约20%;而使用CoT后,即使只有1层Transformer,准确率也达到了100%。
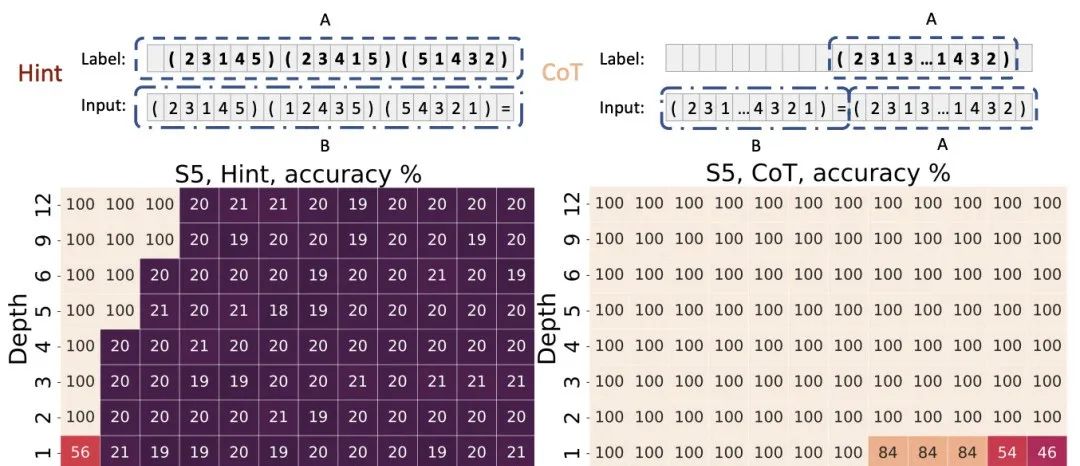
对于迭代平方任务,输入是一个质数p、一个整数r和若干个“^2”符号,输出是r^(2^k) mod p。实验结果与置换群复合任务类似:未使用CoT的情况下,即使是16层Transformer也难以学习;而使用CoT后,1层Transformer就能完美求解。
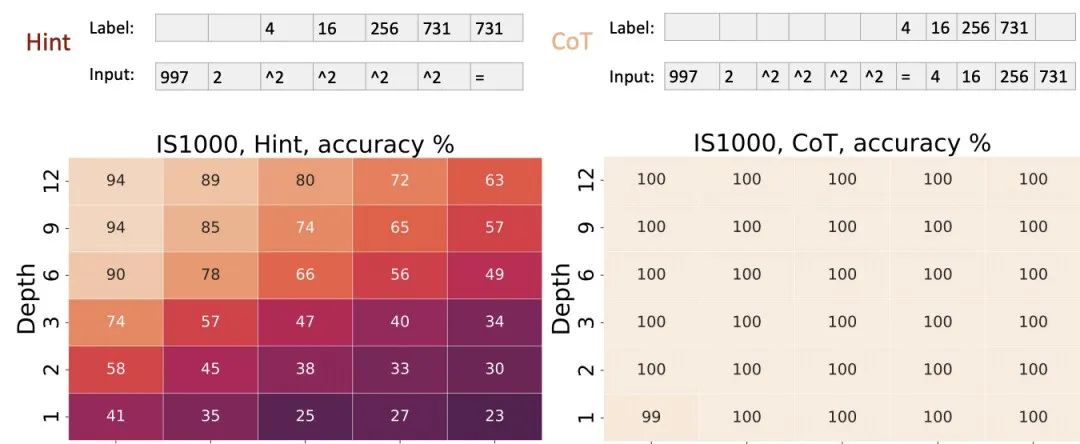
电路值问题的实验结果表明,在基准设置下,4层Transformer的准确率约为50%,8层约为90%,16层接近100%;而使用CoT后,1层Transformer即可达到接近100%的准确率。这验证了CoT赋予了Transformer模拟任意电路的能力,使其能够解决电路值问题这一P完全问题。
CoT+Transformer模拟门电路
除了上述实验,作者还进行了理论证明:
对于任何可以用多项式大小的布尔电路计算的函数,都存在一个仅有常数层数的Transformer,可以通过足够长的思维链(CoT)来模拟电路的计算过程,从而计算出这个函数。
证明的思路是先将布尔电路视为一系列逻辑门的组合,然后利用Transformer中的位置编码为每个逻辑门及其状态分配一个独特的表示,通过逐步计算来模拟整个电路的执行过程。
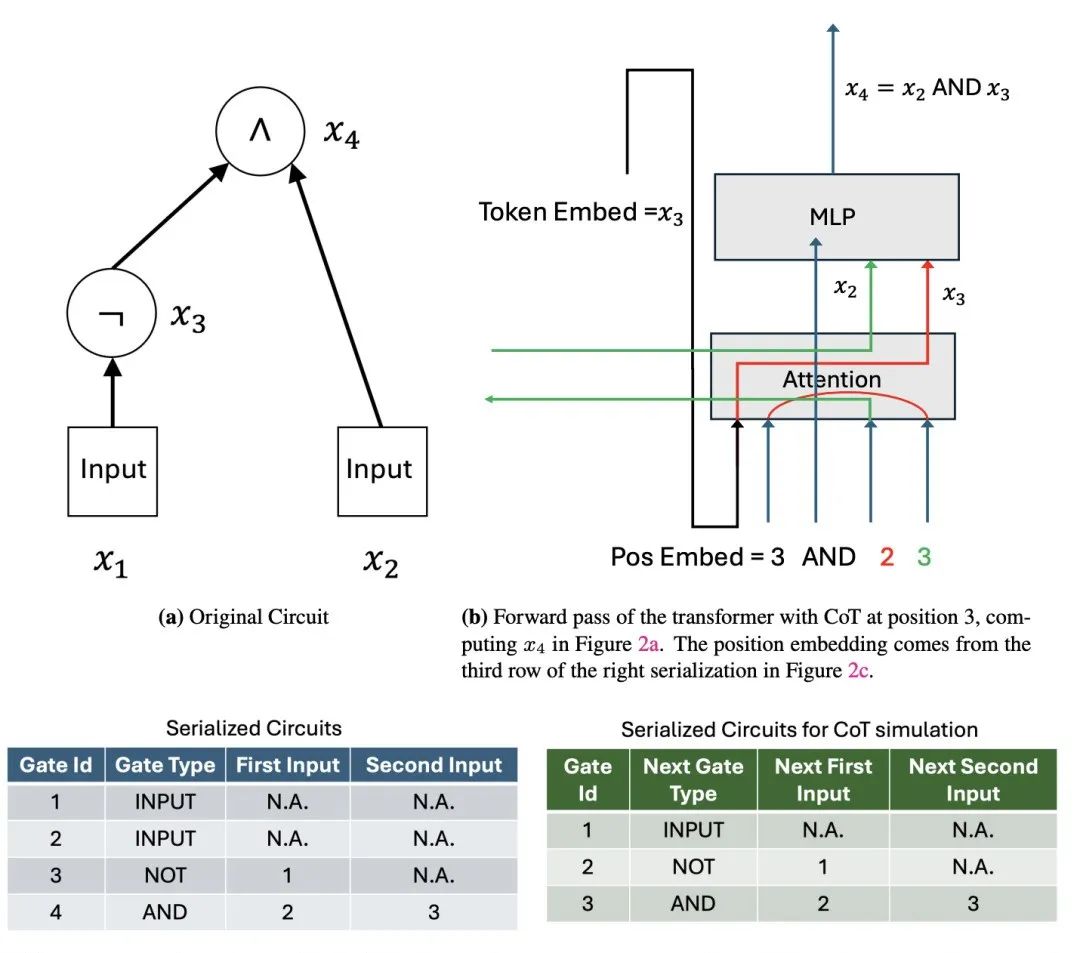
具体而言,对于一个有T(n)个门的电路,作者设计了一个4T(n)个token的输入序列。这个序列包含了电路的完整描述,每个门用4个连续的token表示:门类型、两个输入门的索引和当前门的索引,并用输入序列中的第一个token指示电路的输入值。
作者构造了一个常数深度的Transformer,该Transformer的嵌入维度只需要O(log n),就足以对T(n)个门进行编码。通过将电路“展开”为一个长度为O(T(n))的思维链,Transformer逐步执行电路中的计算,并将中间结果存储在思维链中。最终,最后一个门的输出就对应了电路的最终输出。
在此基础上,作者进一步证明,具有O(T(n))长度CoT的常数深度Transformer,可以模拟任意T(n)大小的电路,因此其计算能力等价于多项式大小的电路。
理论打通,实际可行吗?
能够模拟电路的计算过程,意味着CoT+Transformer能够解决可计算问题。这也说明,只要有足够的CoT思考时间,大模型无需扩展尺寸也能解决复杂问题。
有专业人士用一篇长文解释了CoT和图灵完备性之间的关系:如果没有CoT,Transformer仅限于执行AC0复杂度类中的并行任务;而CoT推理从根本上改变了这一格局,使Transformer能够通过中间推理token处理串行计算,进入P/poly领域。
理论上,只要有足够的CoT步骤,Transformer就能模拟多项式大小电路可以执行的任何计算,缩小与图灵机之间的差距。
然而,实际应用的限制仍然存在,例如有限的上下文窗口和计算资源。要充分利用这一潜力,需要精细的模型设计和优化。

与OpenAI的“草莓”模型的联系
有人将这项成果与OpenAI的“草莓”模型o1联系到了一起——草莓同样是思考时间越长,准确性越高。按照这个思路,只要有好的模型,就有可能解决人类面临的一系列难题。

甚至有人表示,如果这项研究是真的,那么AGI(通用人工智能)就已经在到来的路上了。

然而,也有观点认为这只是一个理论结果,与实际应用还有较大差距。即使忽略理论与实际条件的不同,时间和成本问题也是重要的限制因素。
同时,实验假设模型权重已正确设置,但实际模型的训练很难达到这一程度。此外,这种模拟门电路运算并不是大模型实际学习和工作的方式。如何将实际问题用布尔电路表示,是Transformer从能解决运算问题到实际问题的关键。而现实中,诸如“如何治疗癌症”这类问题,很难以电路的形式去描述。

作者简介
该论文共有四位作者,皆为华人。
按署名顺序,第一位作者是清华姚班校友李志远,他是马腾宇已毕业的博士生,现任芝加哥丰田技术学院(TTIC)的终身助理教授。
第二位作者是Hong Liu,马腾宇的博士生,本科就读于清华,曾获特等奖学金及优秀毕业生荣誉。
第三位是Google Brain推理团队创建者Denny Zhou,他是中科院博士,2017年加入Google前在微软担任了11年的高级研究员。
最后一位是2021年斯隆奖得主、斯坦福大学助理教授马腾宇,他是姚班校友、陈丹琦的同班同学。
论文地址:
https://arxiv.org/abs/2402.12875
参考链接:
[1]https://x.com/denny_zhou/status/1835761801453306089
[2]https://www.reddit.com/r/singularity/comments/1fiemv4/denny_zhou_founded_lead_reasoning_team_at_google/
ChatGPT4o:
谷歌浏览器直接使用:https://www.nezhasoft.cn