原帖
最近校内比较忙,更新缓慢,致歉。

这里函数每次都需要遍历
h
h
h 和
m
m
m 之间的数(复杂度
O
(
n
)
O(n)
O(n)),所以和 solve1 略有不同。仍然假设
T
(
n
)
\operatorname{T}(n)
T(n) 表示
m
−
h
+
1
=
n
m-h+1=n
m−h+1=n 时的复杂度。
T
(
n
)
=
2
×
T
(
n
/
2
)
+
n
=
2
×
(
2
×
T
(
n
/
4
)
+
n
/
2
)
+
n
=
4
×
T
(
n
/
4
)
+
2
n
\operatorname{T}(n)=2\times\operatorname{T}(n/2)+n=2\times(2\times\operatorname{T}(n/4)+n/2)+n=4\times\operatorname{T}(n/4)+2n
T(n)=2×T(n/2)+n=2×(2×T(n/4)+n/2)+n=4×T(n/4)+2n
总结一下规律,就是:
T
(
n
)
=
2
k
×
T
(
n
/
2
k
)
+
k
n
\operatorname{T}(n)=2^k\times\operatorname{T}(n/2^k)+kn
T(n)=2k×T(n/2k)+kn,这里
k
=
l
o
g
2
n
k=log_2n
k=log2n。(假设
k
k
k 是下取整的,造成的误差在计算时间复杂度时可忽略不计)。
T
(
n
)
=
2
k
+
n
k
=
n
+
n
k
\operatorname{T}(n)=2^{k}+nk=n+nk
T(n)=2k+nk=n+nk,相当于
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn) 的复杂度。
时间复杂度计算 递归(solve2 后续)
news2026/2/16 12:22:01
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/2142333.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【C++二叉树】606.根据二叉树创建字符串
606. 根据二叉树创建字符串 - 力扣(LeetCode) 图文分析: 代码实现: 代码说明:
1、前序遍历方式:根-左子树-右子树。
2、题目要求将二叉树转换为字符串输出,所以定义了一个string对象str。
3…
MySQL —— 视图
概念
视图是一张虚拟的表,它是基于一个或多个基本表或其他视图的查询结果集。
视图本身不存储数据,而是通过执行查询来动态生成数据,用户可以像操作普通表一样使用视图来进行查询更新与管理等操作。
视图本身也不占用物理存储空间…
网络安全学习(五)Burpsuite
经过测试,发现BP需要指定的JAVA才能安装。
需要的软件已经放在我的阿里云盘。 (一)需要下载Java SE 17.0.12(LTS)
Java Downloads | Oracle 1.2023版Burp Suite 完美的运行脚本的环境是Java17 2.Java8不支持 看一下是否安装成功,…
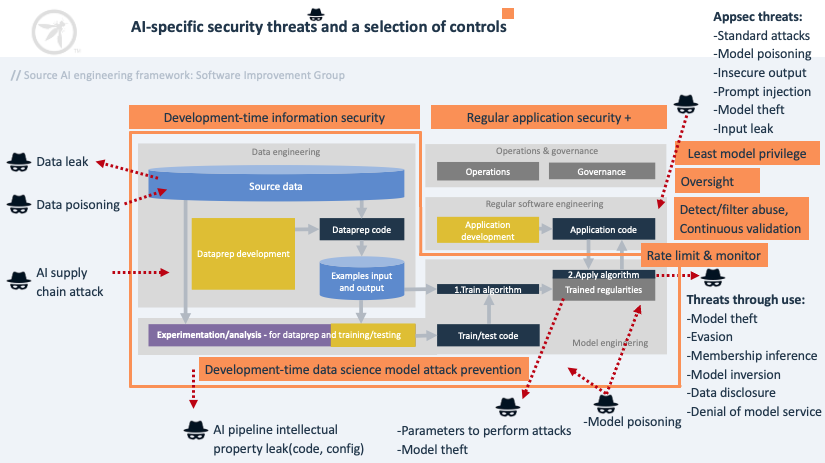
开源AI应用安全指导框架 — OWASP AI Exchange
在当今信息化迅猛发展的时代,网络专业人士正竞相提升人工智能(AI)安全领域的专业技能。随着这一趋势的推进,他们的企业也在快速地引入各类AI工具、平台、应用程序和服务,业界也相应涌现出众多资源,以协助从…
电梯电动车检测-目标检测数据集(包括VOC格式、YOLO格式)
电梯电动车检测-目标检测数据集(包括VOC格式、YOLO格式)
数据集:
链接:https://pan.baidu.com/s/1qRMdF08Jinx_5CRa3al24A?pwd3twc
提取码:3twc 数据集信息介绍: 共有 5347 张图像和一一对应的标注文件 …
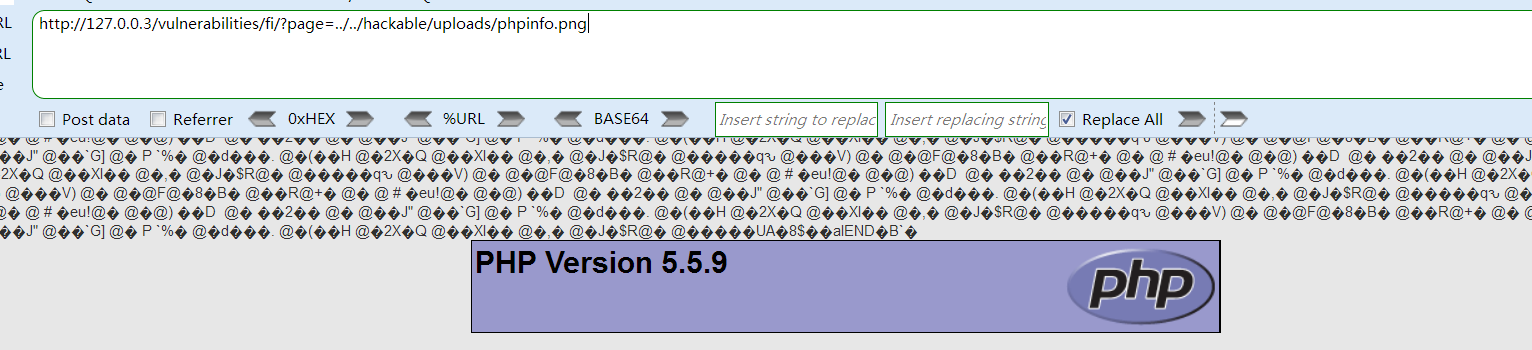
web基础—dvwa靶场(五)File Upload
File Upload(文件上传)
上传的文件对 web 应用程序来说是一个巨大的风险,许多攻击的第一步是上传攻击代码到被攻击的系统上,然后攻击者只需要找到方法来执行代码即可完成攻击。也就是是说,文件上传是攻击者需要完成的第一步。 不受限制的文件…
c#中给winform定义快捷键的几种方式
快捷键的使用在日常的开发中频率比较高,这里总结了最常见的各种快捷键的设置方式,需要的时候大家直接照抄就可以了,不用再去查询如何实现了。 文章目录 一、按钮快捷键二、菜单快捷键三、窗体快捷键四、全局快捷键1、重写ProcessCmdKey2、使…
C++内存管理详解:各类变量的存储区域
在C中,变量的存储位置取决于它们的类型和生命周期。那么不同的各个变量究竟存储在哪个区域呢?
1.不同类型的变量
我们首先从变量类型的不同来说明:
1. 全局变量和静态变量
- 存储区:全局/静态区(静态区࿰…
深度学习----------------------文本预处理
目录 文本预处理读取数据集词源化词表该部分总代码该部分总代码 整合所有功能该部分总代码 文本预处理
文本预处理:把文本当作一个时序序列
将解析文本的常见预处理步骤。 这些步骤通常包括:
①将文本作为字符串加载到内存中。 ②将字符串拆分为词元&…
Redis的存储原理和数据模型
一、Redis是单线程还是多线程呢? 我们通过跑redis的代码,查看运行的程序可以得知,Redis本身其实是个多线程,其中包括redis-server,bio_close_file,bio_aof_fsync,bio_lazy_free,io_t…
Python如何导入自定义包?
在 Python 中,导入包是日常开发的基础操作之一。Python 通过其模块化设计,使得代码可以组织成模块和包,提升了代码的复用性和可维护性。而当开始构建复杂的Python项目时,通常会发现将代码组织在各种模块和包中是非常有帮助的。自定…
【C++】list常见用法
🔥个人主页🔥:孤寂大仙V 🌈收录专栏🌈:C从小白到高手 🌹往期回顾🌹:[C]vector常见用法 🔖 流水不争,争的是滔滔不息。 文章目录 一、list的介绍li…
JVM 调优篇6 可视化性能监控工具-JVisual VM
一 Visual VM
1.1 概述
Visual VM是一个功能强大的多合一故障诊断和性能监控的可视化工具。
它集成了多个JDK命令行工具,使用Visual VM可用于显示虚拟机进程及进程的配置和环境信息(jps,jinfo),监视应用程序的CPU、GC、堆、方法区及线程的信息(jstat…
从0-1 用AI做一个赚钱的小红书账号(不是广告不是广告)
大家好,我是胡广!是不是被标题吸引过来的呢?是不是觉得自己天赋异禀,肯定是那万中无一的赚钱天才。哈哈哈,我告诉你,你我皆是牛马,不要老想着突然就成功了,一夜暴富了,瞬…
信奥初赛解析:1.2-计算机系统的基本结构
目录 知识要点
一、概述
二、计算机硬件系统
(一)处理器
(二)存储器
(1)内存储器
(2)外存储器
①固态硬盘存储器
②机械硬盘存储器
③闪存
(三)输入设备
(四)输出设备
(五)总线结构
(六)主要的性能指标
1.字长
2.运…
计算机毕业设计 网上书店系统 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…
JVM OutOfMemoryError 与 StackOverflowError 异常
目录
前言
堆溢出
虚拟机栈和本地方法栈溢出
方法区溢出 前言 JVM规范中规定, 除了程序计数器之外, 其他的运行时数据区域, 例如堆栈, 方法区, 都会出现OutOfMemoryError异常. 那么到底是怎么样的代码, 才会引起堆溢出, 栈溢出, 或者是方法区的溢出呢? 如果遇到了又该如何…
书生大模型全链路开源体系,学习
优点
书生浦语开源大模型,是一个开源的大模型,大家可以一起学习
还有配套的教学视频,很快就能上手,而且还奖励算力,可以直接训练,讨论学习,非常nice。
教学视频
书生浦语大模型全链路开源开…
FastAPI与环境变量:实现无缝切换与高效运维
在现代软件开发中,尤其是构建RESTful API时,环境变量的管理显得尤为重要。它们不仅允许我们在不同环境中(如开发、测试、生产)灵活地调整应用的行为,还极大地增强了应用的安全性和可维护性。FastAPI作为一个新兴的、高…