差分进化算法（DE算法）求解实例---旅行商问题 (TSP)

一、采用DE求解 TSP
二、旅行商问题
- 2.1 实际例子：求解 6 个城市的 TSP
- 2.2 ==**求解该问题的代码**==
- 2.3 代码运行过程截屏
- 2.4 代码运行结果截屏（后续和其他算法进行对比）
三、 ==如何修改代码？==
- 3.1 减少城市坐标，如下：
- 3.2 增加城市坐标，如下：
四、差分进化算法 (Differential Evolution, DE) 原理
- 4.1 DE算法定义
- 4.2 DE的基本思想
- 4.3 DE的工作原理
- 4.4 DE的参数
- 4.5 DE的优缺点
- - 4.5.1 优点
  - 4.5.2 缺点
- 4.6 DE的应用场景

一、采用DE求解 TSP

求解代码在文中，后续会出其他算法求解TSP问题，你们参加数学建模竞赛只需要会改代码即可。

用来对比此专栏的
遗传算法（GA算法）求解实例—旅行商问题 (TSP)
粒子群算法（PSO算法）求解实例—旅行商问题 (TSP)
模拟退火算法（SA算法）求解实例—旅行商问题 (TSP)
蚁群算法（ACO算法）求解实例—旅行商问题 (TSP)
禁忌搜索算法（TS算法）求解实例—旅行商问题 (TSP)
注意每次运行算法得到的结果可能不太一样。

我知道大家对原理性的东西不感兴趣，我把原理性的东西放在后面，大家如果需要写数模论文可以拿去，但是记得需要改一改，要不然查重过不去。

二、旅行商问题

2.1 实际例子：求解 6 个城市的 TSP

假设有 6 个城市，其坐标如下：

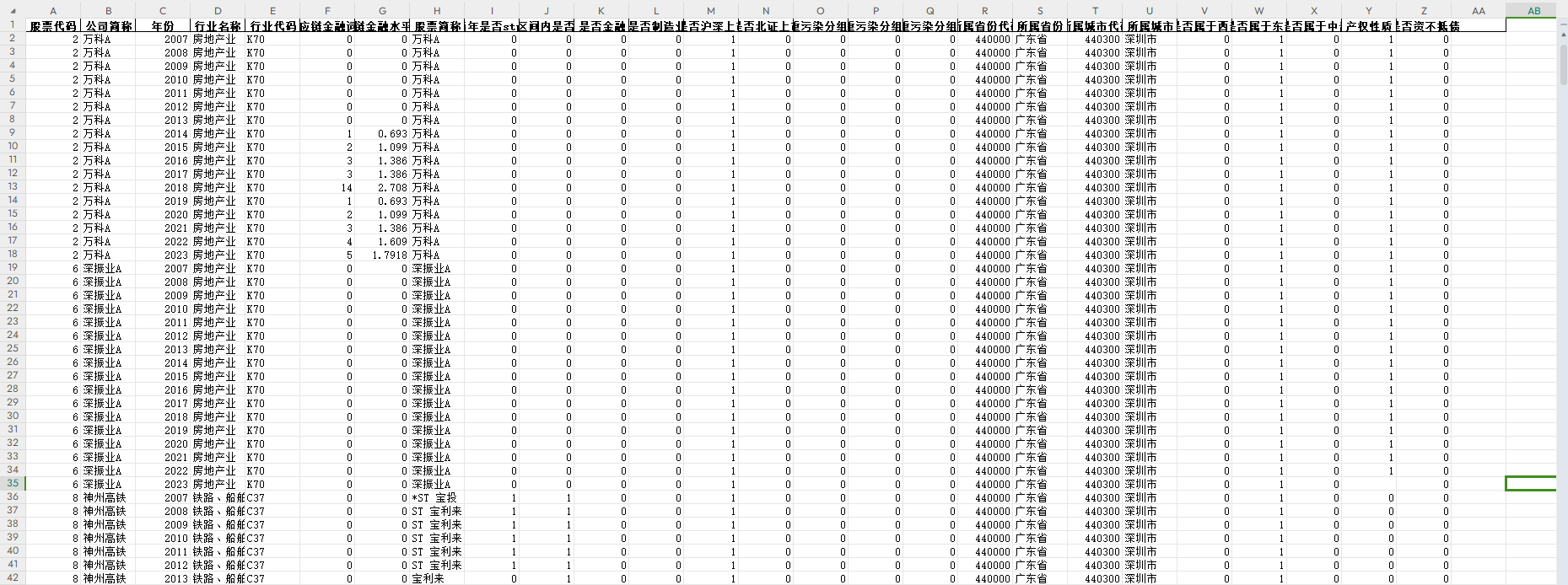
城市	X 坐标	Y 坐标
0	10	20
1	30	40
2	20	10
3	40	30
4	10	10
5	50	20

目标是找到一个经过所有城市且总距离最短的路径。

2.2 求解该问题的代码

import numpy as np
import random

# 定义城市坐标
cities = np.array([
    [10, 20],
    [30, 40],
    [20, 10],
    [40, 30],
    [10, 10],
    [50, 20]
])

# 计算两城市之间的欧几里得距离
def calculate_distance(city1, city2):
    return np.sqrt(np.sum((city1 - city2) ** 2))

# 计算总旅行距离
def total_distance(path):
    distance = 0
    for i in range(len(path) - 1):
        distance += calculate_distance(cities[path[i]], cities[path[i + 1]])
    distance += calculate_distance(cities[path[-1]], cities[path[0]])  # 回到起点
    return distance

# 差分变异操作
def differential_mutation(population, F=0.8):
    size = len(population)
    mutant_population = []
    for i in range(size):
        # 随机选择三个不同的个体
        indices = list(range(size))
        indices.remove(i)
        a, b, c = random.sample(indices, 3)

        # 获取个体的路径
        path_a, path_b, path_c = population[a], population[b], population[c]

        # 生成变异向量 (通过交换生成一个新路径)
        mutant_path = path_a.copy()
        for j in range(len(mutant_path)):
            if random.random() < F:
                # 确保新路径中不出现重复的城市
                if path_b[j] not in mutant_path:
                    mutant_path[j] = path_b[j]
                elif path_c[j] not in mutant_path:
                    mutant_path[j] = path_c[j]

        mutant_population.append(mutant_path)

    return mutant_population

# 差分进化算法主函数
def differential_evolution(cities, pop_size=20, max_iter=500, F=0.8, CR=0.7):
    num_cities = len(cities)

    # 初始化种群（每个个体是一个随机的城市排列）
    population = [list(np.random.permutation(num_cities)) for _ in range(pop_size)]

    # 初始化最优解
    best_solution = population[0]
    best_distance = total_distance(best_solution)

    for iteration in range(max_iter):
        # 差分变异
        mutant_population = differential_mutation(population, F)

        # 交叉与选择
        for i in range(pop_size):
            trial_path = population[i].copy()
            for j in range(num_cities):
                if random.random() < CR:
                    # 采用变异路径的值
                    trial_path[j] = mutant_population[i][j]

            # 修正路径，确保所有城市均被唯一访问
            missing_cities = list(set(range(num_cities)) - set(trial_path))
            for j in range(num_cities):
                if trial_path.count(trial_path[j]) > 1:  # 如果有重复的城市
                    trial_path[j] = missing_cities.pop()  # 替换为缺失的城市

            # 计算试验路径的总距离
            trial_distance = total_distance(trial_path)

            # 选择操作
            if trial_distance < total_distance(population[i]):
                population[i] = trial_path

            # 更新全局最优解
            if trial_distance < best_distance:
                best_solution = trial_path
                best_distance = trial_distance

        print(f"Iteration {iteration + 1}: Best distance = {best_distance:.2f}")

    return best_solution, best_distance

# 运行差分进化算法
best_path, best_distance = differential_evolution(cities)
print("Best path:", best_path)
print("Best distance:", best_distance)

2.3 代码运行过程截屏

在这里插入图片描述

2.4 代码运行结果截屏（后续和其他算法进行对比）

在这里插入图片描述

三、如何修改代码？

这一部分是重中之重，大家参加数学建模肯定是想跑出自己的结果，所以大家只需要把自己遇到的数学问题，抽象成TSP问题，然后修改代码的城市坐标，然后运行即可。

# 定义城市坐标
cities = np.array([
    [10, 20],
    [30, 40],
    [20, 10],
    [40, 30],
    [10, 10],
    [50, 20]
])

3.1 减少城市坐标，如下：

# 定义城市坐标
cities = np.array([
    [10, 20],
    [30, 40],
    [20, 10],
    [40, 30]
])

3.2 增加城市坐标，如下：

# 定义城市坐标
cities = np.array([
    [10, 20],
    [30, 40],
    [20, 10],
    [40, 30],
    [30, 40],
    [20, 10],
    [10, 10],
    [50, 20]
])

四、差分进化算法 (Differential Evolution, DE) 原理

4.1 DE算法定义

差分进化算法 (Differential Evolution, DE) 是一种基于种群的全局优化算法，由 Storn 和 Price 在 1995 年提出。DE 主要用于连续优化问题，但也可以通过适当的修改和适配用于离散问题，如旅行商问题 (TSP)。差分进化算法通过对种群中个体的差分变异、交叉和选择操作，不断逼近问题的最优解。DE 因其简单、高效和全局搜索能力强而受到广泛应用。

4.2 DE的基本思想

差分进化算法的核心思想是通过模拟自然界中的进化过程，对种群中的个体进行变异和选择，以迭代地逼近最优解。算法在每一代中，对种群中的每个个体生成一个“变异个体”，并通过交叉操作形成“试验个体”，然后通过选择操作决定是否用试验个体替换当前个体。

4.3 DE的工作原理

初始化种群：
- 随机生成一个包含多个个体（解）的初始种群，通常个体数量为 pop_size。每个个体表示问题解空间中的一个可能解。
变异操作：
- 对于种群中的每个个体 X_i，生成一个变异个体 V_i。变异是通过随机选择三个不同的个体 X_a、X_b 和 X_c，按如下公式进行：
  $V_i = X_a + F \cdot (X_b - X_c)$
  其中：
  - F 是变异因子，通常取值在 [0, 2] 之间，用于控制差分向量的缩放，影响变异的幅度。
交叉操作：
- 将当前个体 X_i 与其对应的变异个体 V_i 进行交叉操作，生成一个“试验个体” U_i。交叉操作采用以下公式：
  $U_{i,j} = \begin{cases} V_{i,j}, & \text{if } \text{rand}(0, 1) < CR \text{ or } j = j_{rand} \\ X_{i,j}, & \text{otherwise} \end{cases}$
  其中：
  - CR 是交叉概率（交叉率），决定变异个体的分量保留到试验个体中的概率。
  - j_{rand} 是一个随机选择的索引，确保至少一个基因来自变异个体 V_i。
选择操作：
- 选择操作用于决定是否用试验个体 U_i 替换当前个体 X_i。若 U_i 的适应度（即目标函数值）优于 X_i，则用 U_i 替换 X_i：
  $X_i = \begin{cases} U_i, & \text{if } f(U_i) \leq f(X_i) \\ X_i, & \text{otherwise} \end{cases}$
迭代和终止：
- 重复步骤 2-4，直到满足终止条件（如达到最大迭代次数或找到满意解）。

4.4 DE的参数

种群大小 (pop_size)：通常为解空间维度的 5 到 10 倍。较大的种群规模可以提高算法的全局搜索能力，但计算开销也会增加。
变异因子 (F)：控制差分变异的幅度。通常取值在 [0.5, 1.0] 之间。较大的 F 值可能会导致更大的变异，增强全局搜索能力，但可能降低收敛速度。
交叉概率 (CR)：控制交叉操作的概率。通常取值在 [0, 1] 之间。较高的 CR 值会使得个体与变异个体有更多基因交换，增加种群多样性。
最大迭代次数 (max_iter)：算法运行的最大迭代次数，决定了算法的终止条件。