一、算法概念

什么是梯度提升决策树?
  梯度提升决策树（Gradient Boosting Decison Tree）是集成学习中Boosting家族的一员。

  集成学习(ensemble learning)是一种通过组合多个基学习器（模型）来提高整体预测性能的方法。它通过集成多个学习器形成一个强学习器，从而提高模型的泛化能力和准确性。集成学习的核心思想是利用不同模型的组合弥补单一模型的缺点。集成学习可以分为两大类，一类是序列化方法：个体学习器之间存在强依赖关系，必须串行生成，例如boosting；一类是并行化方法：个体学习器之间不存在强依赖关系、可以同时生成，例如bagging（也称为bootstrap聚合）。
  Boosting类算法中最著名的代表是Adaboost算法，Adaboost的原理是，通过前一轮弱学习器的错误率来更新训练样本的权重，不断迭代提升模型性能。
  GBDT与传统的Adaboost算法有显著不同，GBDT同样通过迭代来提升模型的表现，但它采用的是前向分布算法（Forward Stagewise Algorithm），且其弱学习器被限定为CART回归树。此外，GBDT的迭代思想和Adaboost也有所区别。GBDT算法流程如下：

一、算法原理

（一） GBDT 及负梯度拟合原理

  GBDT（Gradient Boosting Decision Tree）是一种利用多个决策树来解决分类和回归问题的集成学习算法。核心思想是通过前一轮模型的残差来构建新的决策树。为了提高拟合效果，Friedman 提出了用损失函数的负梯度来近似残差，从而拟合一个新的CART回归树，负梯度的表示公式为：
$$r_{t,i}=-{\left[\frac{\partial L(y_i,f(x_i))}{\partial f(x_i)}\right]}_{f(x)=f_{t-1}(x)}$$
  其中，$r_{t,i}$表示的是第𝑡轮中，第 𝑖个样本的损失函数的负梯度，𝐿是损失函数，𝑓(𝑥)是模型的预测值。
  在每一轮迭代中，我们首先用样本$(x_i,r_{t,i})$来拟合一棵 CART 回归树。这里 $r_{t,i}$表示的是第 𝑡 轮的负梯度，代表了样本的误差。回归树的每个叶节点会包含一定范围的输入数据，称为叶节点区域 $R_{t,j}$，而叶节点的数量用 J表示。
  每个叶节点输出一个常数值 $c_{t,j}$，它通过最小化损失函数来获得。目标是找到一个 𝑐，使得该节点中的所有样本的损失函数最小化，公式如下所示：
$$c_{t,j}=\arg \underset{c}{\min }\sum _{x_i\in R_{t,j}}L(y_i,f_{t-1}(x_i)+c)$$
  接下来，$h_t(x)$表示为每个叶节点的输出值 $c_{t,j}$的加权和，我们就得到了本轮的决策树拟合函数如下：
$$h_t(x)=\sum _{j=1}^J{c}_{t,j}I(x\in R_{t,j})$$
  其中， $I(x\in R_{t,j})$是一个指示函数，表示样本 𝑥是否属于该叶节点区域 $R_{t,j}$中。
  在每一轮中强学习器是基学习器的更新，通过将当前轮次的决策树的输出叠加到之前的模型上来逐步优化,本轮最终得到的强学习器的表达式如下：
$$f_t(x)=f_{t-1}(x)+\sum _{j=1}^J{c}_{t,j}I(x\in R_{t,j})$$
  无论是分类问题还是回归问题，这种方法都可以通过选择不同的损失函数（例如平方误差或对数损失）来表示模型误差。通过拟合负梯度，模型能够逐步修正误差，从而提高预测精度。

（二） GBDT 回归和分类

1、GBDT回归

  接下来， 可以总结梯度提升决策树（GBDT）的回归算法步骤

  输入训练集样本 T = { ( x , y 1 ) , ( x 2 , y 2 ) , … ( x m , y m ) } T=\left\{\left(x, y_1\right),\left(x_2, y_2\right), \ldots\left(x_m, y_m\right)\right\} T={(x,y1​),(x2​,y2​),…(xm​,ym​)} ，其中，$x_i$是特征，$y_i$是目标变量
  首先，初始化弱学习器在开始时，找到一个常数模型$f_0(x)$ ，通过最小化损失函数 𝐿来获得初始的预测值。这一步可以通过以下公式表示：

$$f_0(x)=\underset{c}{\underbrace{\arg \min }}\sum _{i=1}^{m}L\left(y_i,c\right)$$
  其中，最大迭代次数为 T ，损失函数为 L， 𝑐是一个常数，用来最小化训练集中所有样本的损失函数。
  然后，对迭代轮数 $t=1,2,...,T\dots$ ，执行以下步骤：
  第一步：对样本 $\mathrm{i}=1,2,\dots \mathrm{m}$ ，计算负梯度，即损失函数关于当前模型预测值的导数，表达误差。具体公式如下：
$$r_{ti}=-{\left[\frac{\partial L\left(y_i,f\left(x_i\right)\right))}{\partial f\left(x_i\right)}\right]}_{f(x)=f_{t-1}(x)}$$
表示第 𝑡 轮迭代时，第 𝑖个样本的负梯度。
  第二步：通过样本$x_i,r_{t,i}$拟合一棵 CART 回归树，找到数据的模式并生成叶子节点。
  第三步： 对于回归树的每个叶子节点区域j $=1,2,.$. ，计算最佳拟合值，这个值是通过最小化损失函数 𝐿得到的：
$$c_{tj}=\underset{c}{\underbrace{\arg \min }}\sum _{x_i\in R_{tj}}L\left(y_i,f_{t-1}\left(x_i\right)+c\right)$$
  第四步：更新强学习器，用当前的回归树不断更新强学习器。公式表达如下所示：
$$f_t(x)=f_{t-1}(x)+\sum _{j=1}^J{c}_{tj}I\left(x\in R_{t,j}\right)$$
  其中， 当样本 𝑥位于区域$R_{t,j}$ 时，输出值为 1，否则为 0。这样，新的强学习器通过叠加每一棵回归树的输出来逐步提高预测精度。
  最后，经过 𝑇轮迭代后，我们可以得到强学习树 $f(x)$ ，表达式如下所示：
$$f(x)=f_T(x)=f_0(x)+\sum _{t=1}^T\sum _{j=1}^J{c}_{t,j}I(x\in R_{t,j})$$

1、GBDT分类

  GBDT 的分类算法在思想上与 GBDT 的回归算法类似，但由于分类问题的输出是离散的类别值，而不是连续值，不能像回归那样直接通过输出值来拟合误差。因此，在分类问题中，GBDT 需要采用特殊的处理方法来解决误差拟合的问题，一般有两种处理方式：
  1、使用指数损失函数：
  在这种情况下，GBDT 的分类算法会退化为 Adaboost 算法。这是因为指数损失函数和 Adaboost 使用的误差度量方式非常相似，因此 GBDT 在这种情境下的更新方式与 Adaboost 类似。
  2、使用对数似然损失函数：
  这是更常见的做法，尤其在现代的 GBDT 分类任务中。对数似然损失函数的核心思想是通过样本的预测概率和真实类别之间的差异来拟合损失，而不是直接拟合类别值。
对数似然损失函数的应用类似于逻辑回归中的方法，即使用模型的输出来表示每个类别的预测概率，并计算这种概率与真实类别的匹配度。

二元分类

  在二元分类中，目标是将数据点分类为两个类别之一。GBDT 会输出一个值 p(x)，表示样本属于某一类别的概率。通过最小化负对数似然损失（即逻辑回归中的损失函数）来调整模型，从而提高分类准确性。
  对于二元分类，使用的损失函数为负对数似然损失：
$$L(y,p(x))=-[y\log (p(x))+(1-y)\log (1-p(x))]$$
  其中 p(x) 是模型对样本属于类别 1 的预测概率，y 是样本的真实标签，取值为 0 或 1。
  对于多元分类（即分类类别大于 2 的情况），GBDT 使用类似于 softmax 的损失函数。softmax 函数将模型的输出映射为多个类别的概率分布，然后最小化负对数似然损失来进行优化。

多元分类

  多元分类中的损失函数为：

$$L(y,p(x))=-\sum _{k=1}^K{y}_k\log \left(p_k(x)\right)$$
  其中，K 是类别总数,$y_K$表示样本在类别 k 中的标签值（为 0 或 1）。
  GBDT 的分类算法通过对数似然损失函数来拟合概率值，从而解决分类任务中的误差优化问题。与回归不同，分类中的输出不是直接拟合类别值，而是通过拟合预测概率来实现。这种方式既适用于二元分类，也适用于多元分类任务。

（三）损失函数

  在 GBDT（梯度提升决策树）中，损失函数的选择至关重要，因为它直接决定了模型的优化目标。不同的任务类型（回归、分类等）会使用不同的损失函数。以下是 GBDT 中常用的损失函数：

1、回归问题的损失函数

  平方损失函数 (Mean Squared Error, MSE)：常用于回归问题，度量模型输出与真实值之间的差异。
  定义：
$$L(y,\hat{y})=\frac{1}{2}(y-\hat{y}{)}^2$$
  绝对值损失函数 (Mean Absolute Error, MAE)：也是常见的回归损失函数，使用绝对值误差来度量模型的预测性能。
  定义：
$$L(y,\hat{y})=|y-\hat{y}|$$
  Huber 损失函数：Huber 损失结合了平方损失和绝对值损失的优点，对于离群点有较好的鲁棒性。
  定义：
$$L(y,\hat{y})=\{\begin{array}{ll}\frac{1}{2}(y-\hat{y}{)}^2& \text{ if }|y-\hat{y}|\le \delta \\ \delta \cdot \left(|y-\hat{y}|-\frac{1}{2}\delta \right)& \text{ if }|y-\hat{y}|>\delta \end{array}$$
  分位数损失函数 (Quantile Loss)：适用于分位数回归，可以预测不同分位数的结果。
  定义：
$$L(y,\hat{y})=\{\begin{array}{ll}\alpha (y-\hat{y})& \text{ if }y\ge \hat{y}\\ (1-\alpha )(\hat{y}-y)& \text{ if }y<\hat{y}\end{array}$$

2. 分类问题的损失函数：

  对数似然损失函数 (Logarithmic Loss / Log Loss)：主要用于二元分类问题（类似于逻辑回归），通过最小化预测概率与真实类别之间的差异来优化模型。
定义：
$$L(y,p(x))=-[y\log (p(x))+(1-y)\log (1-p(x))]$$
  多分类对数损失函数 (Multinomial Log-Loss)：用于多分类问题，类似于对数似然损失，但适用于多于两个类别的情况。
  定义：
$$L(y,p(x))=-\sum _{k=1}^K{y}_k\log \left(p_k(x)\right)$$
  指数损失函数 (Exponential Loss)：用于分类问题，尤其是 Adaboost 算法，GBDT 可以通过使用指数损失函数退化为 Adaboost。
定义：
$$L(y,\hat{y})=\exp (-y\hat{y})$$

三、GBDT的优缺点

  GBDT（梯度提升决策树）算法虽然概念不复杂，但要真正掌握它，必须对集成学习的基本原理、决策树的工作机制以及不同损失函数有深入理解。目前，性能较为优异的 GBDT 库有 XGBoost，而 scikit-learn 也提供了 GBDT 的实现。

（一）优点

• 处理多类型数据的灵活性：GBDT 可以同时处理连续值和离散值，适应多种场景。
• 高准确率且相对少的调参：即使花费较少的时间在调参上，GBDT也能在预测准确率上有较好表现，尤其是相对于 SVM。
• 对异常值的鲁棒性：通过使用健壮的损失函数，如 Huber损失函数和分位数损失函数，GBDT 对异常数据有很强的鲁棒性。

（二）缺点

• 难以并行化训练：由于 GBDT 中的弱学习器（决策树）存在依赖关系，导致训练时难以并行化。不过，部分并行化可以通过使用自采样的 SGBT方法来实现。
• 训练时间较长：由于迭代的特性和逐步拟合的过程，GBDT 的训练速度相比一些其他算法较慢。

四、GBDT分类任务实现对比

  主要根据模型搭建的流程，对比传统代码方式和利用Sentosa_DSML社区版完成机器学习算法时的区别。

（一）数据加载

1、Python代码

from sklearn.datasets import load_iris

# 加载数据集
iris = load_iris()
X = iris.data  # 特征
y = iris.target  # 标签

2、Sentosa_DSML社区版

  利用文本读入算子对数据进行读取。

（二）样本分区

1、Python代码

from sklearn.model_selection import train_test_split

# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

2、Sentosa_DSML社区版

  利用样本分区算子对数据集进行划分。

  利用类型算子设置数据的特征列和标签列

（三）模型训练

1、Python代码

from sklearn.ensemble import GradientBoostingClassifier

# 创建 Gradient Boosting 分类器
gbdt_classifier = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)

# 训练 GBDT 模型
gbdt_classifier.fit(X_train, y_train)

# 进行预测
y_pred = gbdt_classifier.predict(X_test)

2、Sentosa_DSML社区版

  连接模型算子并选择模型参数

  执行得到模型的训练结果

（二）模型评估

1、Python代码

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

# 评估模型
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='weighted')
recall = recall_score(y_test, y_pred, average='weighted')
f1 = f1_score(y_test, y_pred, average='weighted')

# 打印评估结果
print(f"GBDT 模型的准确率: {accuracy:.2f}")
print(f"加权精度 (Weighted Precision): {precision:.2f}")
print(f"加权召回率 (Weighted Recall): {recall:.2f}")
print(f"F1 值 (Weighted F1 Score): {f1:.2f}")

# 生成混淆矩阵
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', xticklabels=iris.target_names, yticklabels=iris.target_names)
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.title('Confusion Matrix')
plt.show()

2、Sentosa_DSML社区版

  连接评估算子对模型进行评估

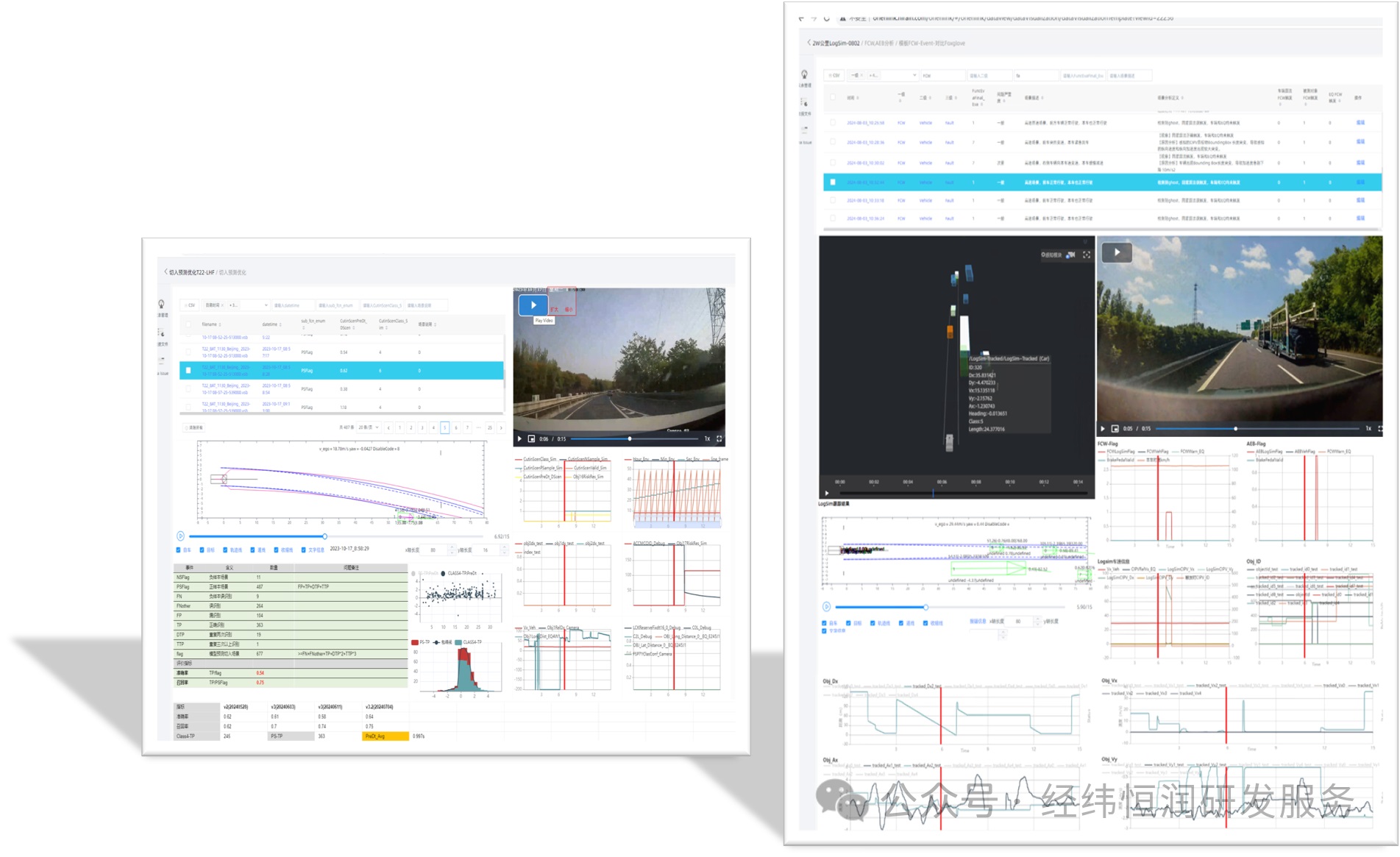
得到训练集和测试集的评估结果

  连接混淆矩阵算子计算模型混淆矩阵

  得到训练集和测试集的混淆矩阵结果

（二）模型可视化

1、Python代码

# 计算特征重要性并进行排序
importances = gbdt_classifier.feature_importances_
indices = np.argsort(importances)[::-1]  # 按特征重要性降序排列索引

# 绘制特征重要性柱状图
plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align="center")
plt.xticks(range(X.shape[1]), [iris.feature_names[i] for i in indices], rotation=45)  # 使用特征名称
plt.tight_layout()
plt.show()

# 决策树的可视化
# 获取 GBDT 模型的其中一棵决策树
estimator = gbdt_classifier.estimators_[0, 0]  # 获取第一轮的第一棵树
plt.figure(figsize=(20, 10))
tree.plot_tree(estimator, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True)
plt.title('Decision Tree Visualization (First Tree in GBDT)')
plt.show()

2、Sentosa_DSML社区版

  右键查看模型信息即可得到模型特征重要性，决策树可视化等结果：

  特征重要性、混淆矩阵、GBDT 模型的决策树划分和其中一棵决策树结果如下所示：

五、GBDT回归任务实现对比

（一）数据加载、样本分区和特征标准化

1、Python代码

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
from sklearn import tree

# 读取数据集
df = pd.read_csv("D:/sentosa_ML/Sentosa_DSML/mlServer/TestData/winequality.csv")

# 将数据集划分为特征和标签
X = df.drop("quality", axis=1)  # 特征，假设标签是 "quality"
Y = df["quality"]  # 标签

# 划分训练集和测试集
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

# 标准化特征
sc_x = StandardScaler()
X_train = sc_x.fit_transform(X_train)
X_test = sc_x.transform(X_test)

2、Sentosa_DSML社区版

  利用文本算子读入数据

连接样本分区算子，划分训练集和测试集

  连接类型算子将“quality”列设为标签列。

  连接标准化算子进行特征标准化

（二）模型训练

1、Python代码

# 训练梯度提升决策树回归器
gbdt_regressor = GradientBoostingRegressor(n_estimators=500, learning_rate=0.1, max_depth=10, random_state=42)
gbdt_regressor.fit(X_train, Y_train)

# 预测测试集上的标签
y_pred = gbdt_regressor.predict(X_test)

2、Sentosa_DSML社区版

  在标准化结束后，选择梯度决策树回归算子，进行参数配置后，点击执行。

  完后执行之后，我们可以得到梯度提升决策树模型。

（三）模型评估

1、Python代码

# 计算评估指标
r2 = r2_score(Y_test, y_pred)
mae = mean_absolute_error(Y_test, y_pred)
mse = mean_squared_error(Y_test, y_pred)
rmse = np.sqrt(mse)
mape = np.mean(np.abs((Y_test - y_pred) / Y_test)) * 100
smape = 100 / len(Y_test) * np.sum(2 * np.abs(Y_test - y_pred) / (np.abs(Y_test) + np.abs(y_pred)))

# 打印评估结果
print(f"R²: {r2}")
print(f"MAE: {mae}")
print(f"MSE: {mse}")
print(f"RMSE: {rmse}")
print(f"MAPE: {mape}%")
print(f"SMAPE: {smape}%")

2、Sentosa_DSML社区版

  连接评估算子对模型进行评估

  训练集评估结果

  测试集评估结果

（四）模型可视化

1、Python代码

# 可视化特征重要性
importances = gbdt_regressor.feature_importances_
indices = np.argsort(importances)[::-1]

plt.figure(figsize=(10, 6))
plt.title("Feature Importances")
plt.bar(range(X.shape[1]), importances[indices], align="center")
plt.xticks(range(X.shape[1]), X.columns[indices], rotation=45)
plt.tight_layout()
plt.show()

2、Sentosa_DSML社区版

  右键查看模型信息即可得到模型特征重要性，决策树可视化等结果：

六、总结

  相比传统代码方式，利用Sentosa_DSML社区版完成机器学习算法的流程更加高效和自动化，传统方式需要手动编写大量代码来处理数据清洗、特征工程、模型训练与评估，而在Sentosa_DSML社区版中，这些步骤可以通过可视化界面、预构建模块和自动化流程来简化，有效的降低了技术门槛，非专业开发者也能通过拖拽和配置的方式开发应用，减少了对专业开发人员的依赖。
  Sentosa_DSML社区版提供了易于配置的算子流，减少了编写和调试代码的时间，并提升了模型开发和部署的效率，由于应用的结构更清晰，维护和更新变得更加容易，且平台通常会提供版本控制和更新功能，使得应用的持续改进更为便捷。

  为了非商业用途的科研学者、研究人员及开发者提供学习、交流及实践机器学习技术，推出了一款轻量化且完全免费的Sentosa_DSML社区版。以轻量化一键安装、平台免费使用、视频教学和社区论坛服务为主要特点，能够与其他数据科学家和机器学习爱好者交流心得，分享经验和解决问题。文章最后附上官网链接，感兴趣工具的可以直接下载使用

https://sentosa.znv.com/