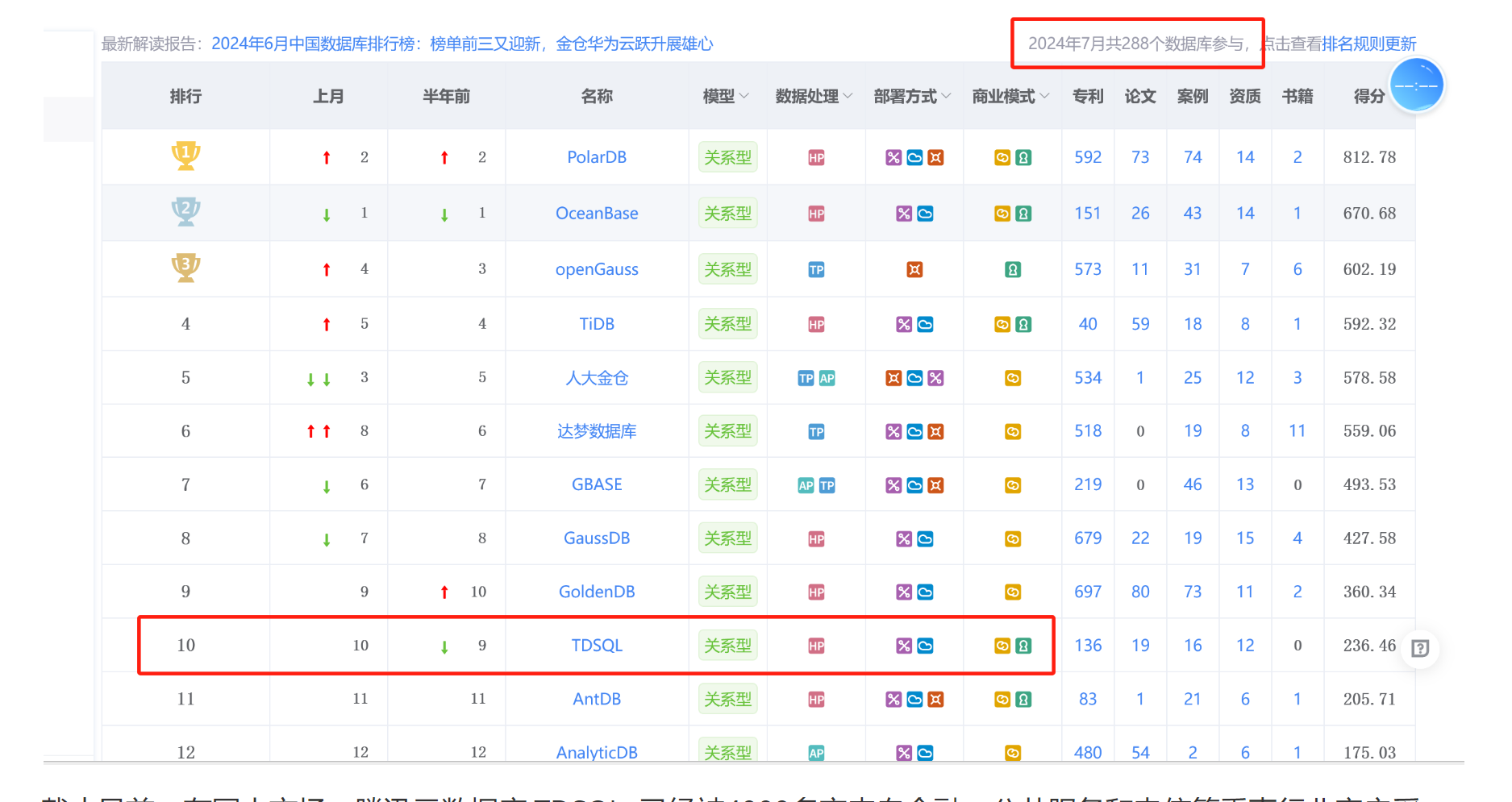
LEAN论文在证明赋型唯一性（Unique Typing ）时，引入了 n-provability 的概念，通过证明在 n-provability 情况下的赋型唯一性，来证明系统的 赋型唯一性。同时，在证明在 n-provability 情况下的赋型唯一性时，引入了 κ 简化（κ reduction）的概念，以及 Church-Rosser 推论（Church-Rosser theorem）。

        其证明过程如下引用所示：

       其中，

        最终要证明的是：

        需要通过对表达式e 计算（Computation / Normalization）过程中的，赋型规则与定义上相等规则的切换次序作为归纳步骤（Inductive Step），进行归纳证明（Induction on the number of alternatives between the judgments Γ ⊢ e:α and Γ ⊢ α ≡ β ）。

        这是因为，表达式e 的计算过程中，e 的表达式形态变换是根据定义上相等规则进行的，其对应的类型形态也随之根据对应的定义上相等规则来变换，同时对形变后的e根据赋型规则进行赋型。

        这样，赋型规则与定义上相等规则的切换使用就覆盖整个表达式 e 的计算过程。由此，证明了，e 的计算过程中，其类型的变换都是定义上相等的，即赋型唯一性（Unique Typing）。

        此时，赋型唯一性就可以说成，如果 表达式 e 经过多次形变后，有 Γ ⊢ₙ e:α 和 Γ ⊢ₙ e:β，那么，最终两个类型，α 和 β，在定义上相等（Defintional Equal），记 Γ ⊢ₙ₊₁ α ≡ β。此时，LEAN中需要给定 n-provability  ⊢ₙ 是 定义上反向的（Definitional Inversion）。这是，因为 在证明唯一性的过程，使用的定义上相等规则需要保持其唯一性，即 前提有结论 的同时，结论有前提，也就是说，只存在唯一的规则，能得出该结论。从而使得整个类型系统的运作，其赋型的唯一性。

        定义上反向（Definitional Inversion）为：

        然后通过证明，第0步和第 n+1步的定义上反向的，从而归纳证明整个 n-provability  ⊢ₙ 是 定义上反向的（Definitional Inversion），即整个表达式e 的形变过程中，特定的定义上相等的规则，是定义上反向的（Definitional Inversion）。

        在证明 第 n+1步的定义上反向时，需要表达式 e 形变的过程，只使用了 K 简化规则（K Reduction），即 β δ ζ ι 简化。

        同时，要有，当表达式 e 在形变的过程中，有不同路径进行，最终会形变成同一个定义上相等的表达式。

       

到此，上述就是，LEAN给出的赋型唯一性的证明步骤。其中，详细的证明过程可查看原文。后面，会有相关文章对上述引入的概念及相关证明，进行梳理及注解。