描述

给定一个 n * m 的矩阵 a，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，输出所有的路径中最小的路径和。

数据范围: 1≤n,m≤500，矩阵中任意值都满足 0≤ai,j≤100

要求：时间复杂度 O(nm)

例如：当输入[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]时，对应的返回值为12，

所选择的最小累加和路径如下图所示：

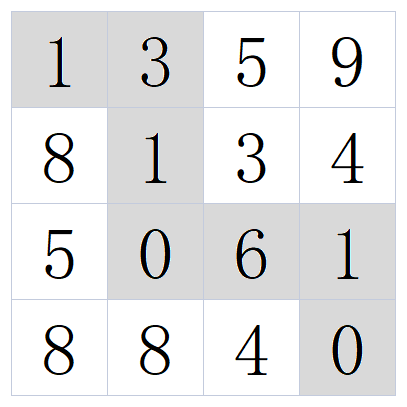
示例1

输入：

[[1,3,5,9],[8,1,3,4],[5,0,6,1],[8,8,4,0]]

返回值：

12

示例2

输入：

[[1,2,3],[1,2,3]]

返回值：

7

思路分析：

该题可以使用动态规划进行求解：

创建一个比原矩阵多一行一列的二维数组temp，这样做是为了方便处理边界条件，避免在后续计算中需要特别检查是否越界。

然后对第一行和第一列进行初始化

那么取其中较小值与当前位置的值相加就是到当前位置的最小路径和，

因此状态转移公式为dp[i][j]=min(dp[i−1][j],dp[i][j−1])+matrix[i][j]

代码：

import java.util.*;
public class Solution {
    /**
     * @param matrix int整型二维数组 the matrix
     * @return int整型
     */
    public int minPathSum (int[][] matrix) {
        int row=matrix.length;//行
        int column=matrix[0].length;
        int[][] temp=new int[row+1][column+1];
        temp[0][0]=matrix[0][0];
        //第一行
        for(int i=1;i<row;i++){
            temp[i][0]=matrix[i][0]+temp[i-1][0];
        }
        //第一列
        for(int j=1;j<column;j++){
            temp[0][j]=matrix[0][j]+temp[0][j-1];
        }

        for(int i=1;i<row;i++){
            for(int j=1;j<column;j++){
                if(temp[i][j-1]<temp[i-1][j]){
                    temp[i][j]=temp[i][j-1]+matrix[i][j];
                }else{
                    temp[i][j]=temp[i-1][j]+matrix[i][j];
                }
            }
        }
        return temp[row-1][column-1];
    }
}