多目标规划

多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。又称多目标最优化。通常记为 MOP(multi-objective programming)。

多目标规划的概念是 1961年由美国数学家查尔斯和库柏首先提出的。多目标最优化思想，最早是在1896年由法国经济学家V.帕雷托提出来的。他从政治经济学的角度考虑把本质上是不可比较的许多目标化成单个目标的最优化问题，从而涉及了多目标规划问题和多目标的概念。

1. 模型原理

1.1 多目标规划的一般形式

多目标规划是多目标决策的重要内容之一，在进行多目标决策时，当希望每个目标都尽可能的大(或尽可能够小)时，就形成了一个多目标规划问题，其一般形式为：
$$\begin{array}{rl}\min & \mathrm{f}(\mathrm{x})=[{\mathrm{f}}_1(\mathrm{x}),{\mathrm{f}}_2(\mathrm{x}),\cdots ,{\mathrm{f}}_{\mathrm{m}}(\mathrm{x}){]}^{\mathrm{T}},\\ s.t.& \{\begin{array}{ll}{\mathrm{g}}_{\mathrm{i}}(\mathrm{x})\le 0,& \mathrm{i}=1,2,\cdots ,\mathrm{p},\\ {\mathrm{h}}_{\mathrm{j}}(\mathrm{x})=0,& \mathrm{j}=1,2,\cdots ,\mathrm{q},\end{array}\end{array}$$

• 其中$x$为决策向量，$f_1(x),f_2(x),\cdots ,f_m(x)$为目标函数s.$t.$式为约束条件
• 记 Ω = { x ∣ g i ( x ) ≤ 0 , i = 1 , 2 , ⋯   , p ; h j ( x ) = 0 , j = 1 , 2 , ⋯   , q } \begin{aligned}&\text{记}\Omega=\{x|g_{i}(x)\leq0, i=1,2,\cdots,p; h_{j}(x)=0, j=1,2,\cdots,q\}\end{aligned} ​记Ω={x∣gi​(x)≤0,i=1,2,⋯,p;hj​(x)=0,j=1,2,⋯,q}​
• 称$\Omega$为多目标规划的可行域(决策空间)，$f(\Omega )=$ { f ( x ) ∣ x ∈ Ω } \{f(x)|x\in\Omega\} {f(x)∣x∈Ω}为多目标规划问题的像集(目标空间)，多目标规划问题以下简称问题(MP)。

1.2 多目标规划的解

• 最优解定义

  设$\bar{x}\in \Omega$, 若对于任意$i=1,2,\cdot \cdot \cdot ,m$及任意$x\in \Omega$,均有
  $$f_i(\bar{x})\le f_i(x)$$
  则称$\bar{x}$为问题(MP)的绝对最优解，记问题(MP)的绝对最优解集为${\Omega }_{\mathrm{ab}}^{\ast }$

  一般来说，多目标规划问题的绝对最优解是不常见的，当绝对最优解不存在时，需要引入新的“解”的概念。多目标规划中最常用的解为非劣解或有效解，也称为Pareto最优解。

• 有效解定义

  考虑多目标规划问题(MP),设$\bar{x}\in \hat{\Omega }$,若不存在$x\in \hat{\Omega }$,使得
  $$f_i(x)\le f_i(\bar{x}),i=1,2,\cdots ,m,$$
  且至少有一个
  $$f_j(x)<f_j(\bar{x}),$$
  则称$\bar{x}$为问题(MP)的有效解(或Pareto有效解)，$f(\bar{x})$为有效点。

• 满意解定义

  主要是从决策过程角度,根据决策者的偏好与要求而提出的。设可行域为$\Omega$，要求$m$个目标函数$f_i(i=1,2,\cdots ,m)$越小越好。有时决策者的期望较低,给出了$m$个阈值${\alpha }_i$， 当$\bar{x}\in \Omega$满足$f_i(\bar{x})\le {\alpha }_i(i=1,2,\cdots ,m)$时,就认为$\bar{x}$是可以接受的、是满意的。这样的$\bar{x}$就称为一个满意解。

1.3 多目标规划的求解

由于对绝大多数多目标决策实际问题，决策者最偏好的方案都是有效解，下面介绍几种常用的求解问题(MP)的有效解的常用方法

值得注意的是，在多目标规划中，除去目标函数一般是彼此冲突外，还有另一个特点：目标函数的不可公度性。所以通常在求解前,先对目标函数进行预处理。预处理的内容包括:无量纲化处理,归一化处理等

MP问题求解有效解的常用方法

• 线性加权法

  该方法的基本思想是根据目标的重要性确定一个权重，以目标函数的加权平均值为评价函数，使其达到最优。权重的确定一般由决策者给出，因而具有较大的主观性，不同的决策者给的权重可能不同，从而会使计算的结果不同。

• $\epsilon$约束法

  根据决策者的偏好，选择一个主要关注的参考目标，而将其他目标函数放到约束条件中。约束法也称主要目标法或参考目标法，参数E是决策者对变为约束条件的目标函数的容许接受阈值。

• 理想点法

  该方法的基本思想是：以每个单目标最优值为该目标的理想值，使每个目标函数值与理想值的差的加权平方和最小。

• 优先级法

  该方法的基本思想是根据目标重要性分成不同优先级，先求优先级高的目标函数的最优值，在确保优先级高的目标获得不低于最优值的条件下，再求优先级低的目标函数

线性加权法详解：

若一个规划问题中有多个目标，我们可以对多目标函数进行加权组合使问题变为单目标规划，然后再利用之前学习的解法进行求解

线性加权法具体步骤如下：

1. 确定每个目标的权系数。

$$0\le w_j\le 1,j=1,2,\cdots ,m;\sum _{j=1}^m{w}_j=1$$

2. 写出评价函数
   $$\sum _{j=1}^m{w}_j{f}_j$$

3. 求评价函数最优值
   $$\begin{array}{ll}min& {\sum }_{i=1}^m{w}_i{f}_i(x),\\ s.t.& \mathbf{x}\in \mathbf{\Omega }.\end{array}$$

注意：

1. 要将多个目标函数统一为最大化和最小化问题(不同的加“-” 号)才可以进行加权组合
2. 如果目标函数量纲不同，则需要对其进行标准化再进行加权，标准化的方法一般是目标函数除以某一个常量，该常量是这个目标函数的某个取值，具体取何值可根据经验确定
3. 对多目标函数进行加权求和是，权重一般由该领域专家给定，实际比赛中，若无特殊说明，我们可令权重相同

2. 典型例题

某化工厂今年拟生产两种新产品A和B，其生产费用分别为2万元/吨和5万元/吨。这两种产品均将造成环境污染，每生产一吨A产品会产生0.4吨的污染，每生产一吨B产品会产生0.3吨的污染。由于条件限制，工厂生产产品A和B的最大生产能力各为每月5吨和6吨，而市场需要这两种产品的总量每月不少于7吨。该工厂决策认为，这两个目标中环境污染应该优先考虑，且根据经验生产费用的参考值为30万元，污染量参考值为2吨。试问工厂如何安排生产计划，在满足市场需要的前提下，使设备的花费和产生的污染均达到最小。

设工厂每月产品A生产$x_1$吨，B生产$x_2$吨，那么产生的污染分别为0.4$x_1$吨和0.3$x_2$吨

建立多目标规划模型：
$$\{\begin{array}{l}\min f_1=2x_1+5x_2\\ \min f_2=0.4x_1+0.3x_2\\ st.\{\begin{array}{l}{x}_1+x_2\ge 7\\ 0\le x_1\le 5\\ 0\le x_2\le 6\end{array}\end{array}$$
下面我们将其转换为一个单目标规划问题，即对上面的两个目标函数进行加权，由于该工厂决策认为环境污染应优先考虑，因此我们可以选取$f_1$和$f_2$的权重分别为0.4和0.6。注意到两个目标函数的单位不同，一个为“万元”,一个为“吨”,因此我们需要首先对目标函数进行标准化来消除量纲的影响，然后再进行加权，由于题目中已经给了产品费用和污染量的参考值，因此我们将这两个目标函数分别除以其参考值来消除量纲。

加权后的目标函数：
$$f=0.4\times \frac{f_1}{30}+0.6\times \frac{f_2}{2}=\frac{0.4}{30}\times (2x_1+5x_2)+\frac{0.6}{2}\times (0.4x_1+0.3x_2)$$
敏感性分析：

下面我们对结果进行敏感性分析，敏感性分析是指从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。其实质是通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小的规律。

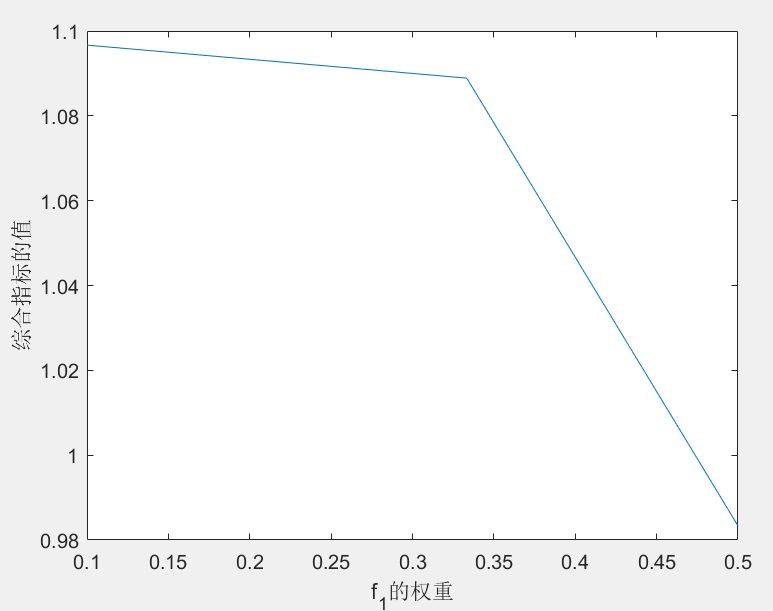
我们改变$f_1$和$f_2$的权重，来观察对结果的影响。(由于两个权重和为1，因此我们只需要改变$f_1$的权重即可)，下面是图形：

可以看出，$f_1$的权重的转折点在0.333-0.334之间，当$f_1$的权重小于这个转折点时，$x_1=1,x_2=$ 6,大于转折点时，$x_1=5,x_2=2$。其主要原因是：当$f_1$的权重越小时，厂家对环境污染的权重就越大，那么厂家就更加倾向于生产污染较少的产品B，尽管B的生产费用要远高于产品A。

3. matlab代码实现

多目标规划模型的求解

%% 多目标规划问题
clc
clear
% 两个目标权重
w1=0.4;
w2=0.6;
c=[w1/30*2+w2/2*0.4;w1/30*5+w2/2*0.3];
% 不等式约束
A=[-1,-1];
b=-7;
% 上下界
lb=[0 0]';
ub=[5 6]';
% 求解
[x,fval]=linprog(c,A,b,[],[],lb,ub)
f1=2*x(1)+5*x(2)
f2=0.4*x(1)+0.3*x(2)

输出：

找到最优解。


x =

     5
     2


fval =

    1.0467


f1 =

    20


f2 =

    2.6000

敏感性分析：

%% 敏感性分析
clear
clc
W1=0.1:0.001:0.5;
W2=1-W1;
n=length(W1);
F1=zeros(n,1);
F2=zeros(n,1);
X1=zeros(n,1);
X2=zeros(n,1);
FVAL=zeros(n,1);
A=[-1,-1];
b=-7;
lb=[0 0];
ub=[5 6];
for i=1:n
    w1=W1(i);
    w2=W2(i);
    c=[w1/30*2+w2/2*0.4;w1/30*5+w2/2*0.3];
    [x,fval]=linprog(c,A,b,[],[],lb,ub);
    F1(i)=2*x(1)+5*x(2);
    F2(i)=0.4*x(1)+0.3*x(2);
    X1(i)=x(1);
    X2(i)=x(2);
    FVAL(i)=fval;
end
figure(1)
plot(W1,F1,W1,F2)
xlabel('f_{1}的权重')
ylabel('f_{1}和f_{2}的取值')
legend('f_{1}','f_{2}')

figure(2)
plot(W1,X1,W1,X2)
xlabel('f_{1}的权重')
ylabel('x_{1}和x_{2}的取值')
legend('x_{1}','x_{2}')

figure(3)
plot(W1,FVAL)% 看起来是两个直线组合起来的下半部分
xlabel('f_{1}的权重')
ylabel('综合指标的值')

输出：

figure1:

figure2:

figure3: