1.10 DFT示例2

1.10.2 一个通用正弦波

通过将复正弦波的表达式代入DFT的定义，并按照矩形序列示例中的相同步骤，可以类似地推导出通用正弦波的DFT。

尽管如此，在理解了上述概念后，我们可以通过一种更简单的方法看到一般正弦波的离散傅里叶变换（DFT）的幅度和相位图的样子。因为全为1的矩形序列实际上是一个频率为0、长度为$L=N$ 的复正弦波，所以一般复正弦波的DFT幅度可以通过在方程（1.67）的sinc信号中，将$L=N$（因为它跨越了整个长度）、$n_s=0$（从0开始），以及用$k-k^{\prime }$代替$k$ 来计算（使sinc中心对齐到零）：

$$|S[k]| = \frac{\sin(\pi(k - k'))}{\sin(\pi(k - k')/N)}$$$$\angle S[k] = -2\pi \frac{k - k'}{N} \left(\frac{N - 1}{2}\right) \tag{1.70}$$

类似地，实数正弦波 $\cos \left[2\pi \left(k^{\prime }/N\right)n\right]$ 的DFT可以看作是上述表达式的和，其中将 $k-k^{\prime }$ 替换为 $k+k^{\prime }$，因为每个实数正弦波由两个复数正弦波组成，并且缩放了一半，参见方程 (1.27)。

例如，考虑图1.68中显示的信号，它由两个频率分别为1 kHz 和 2 kHz 的正弦波组成，如下所示：

$$s(t) = s_1(t) + s_2(t)$$$$= \sin(2\pi 1000t) + 0.75 \sin(2\pi 2000t + 120^\circ)$$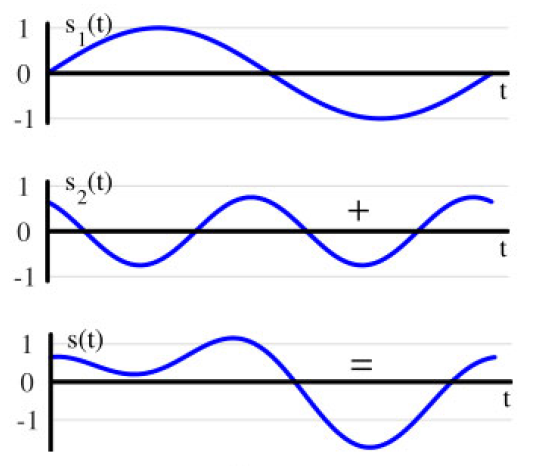

​​

图 1.68: 一个由两个正弦波组成的信号 $s(t)$

上述信号以采样率 $1/T_S=F_S=8$ kHz 生成：

$$s[n] = \sin(2\pi1000nT_S) + 0.75 \sin(2\pi2000nT_S + 120^\circ)$$$$= \sin\left( 2\pi \frac{1}{8} n \right) + 0.75 \sin\left( 2\pi \frac{2}{8} n + 120^\circ \right) \quad (1.71)$$

我们DFT分析的频率 $F=F_S(k/N)$ 对于一个8点的DFT，结果为：

• 当 $k=0$: $8000\cdot \frac{0}{8}=0$ kHz
• 当 $k=\pm 1$: $8000\cdot \frac{\pm 1}{8}=\pm 1$ kHz
• 当 $k=\pm 2$: $8000\cdot \frac{\pm 2}{8}=\pm 2$ kHz
• 当 $k=\pm 3$: $8000\cdot \frac{\pm 3}{8}=\pm 3$ kHz

因此，在这种情况下，频段 1 对应于实际频率 1 kHz，频段 2 对应 2 kHz，依此类推。DFT $S[k]$ 的 IQ 形式和幅度相位图如图 1.69 所示。

​​

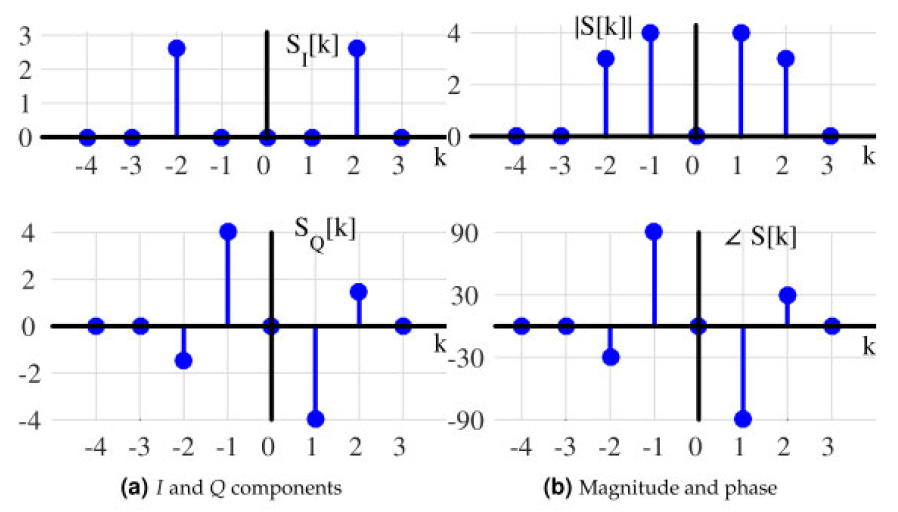
图 1.69: 由两个正弦波组成的 $s[n]$ 的 DFT

从图的幅度图中可以观察到，DFT检测到了信号中的两个实际正弦波，因为在频段 1 和 -1 处的脉冲指示了两个复数正弦波的存在，这些复数正弦波组合形成了频率为 $8000\cdot \frac{1}{8}=1$ kHz 的一个实数正弦波。类似的情况适用于另一频率 2 kHz 的正弦波。

直流或平均值

该信号的直流（DC）或平均值 $\frac{1}{N}\sum s[n]$ 为0，这可以从方程（1.71）中看出，因为正弦波在整数个周期上的平均值为0。

幅度

当输入信号包含一个峰值幅度为 $A$ 且在 $N$ 个输入样本中具有整数个周期的复正弦波时，该特定正弦波的离散傅里叶变换（DFT）的输出幅度为 $AN$。这可以通过将幅度为 $A_0$ 的复正弦波的表达式代入DFT定义来验证。

$$I \rightarrow \sum_{n=0}^{N-1} \left[ A_0 \cos \frac{2 \pi k}{N} n \cdot \cos \frac{2 \pi k}{N} n + A_0 \sin \frac{2 \pi k}{N} n \cdot \sin \frac{2 \pi k}{N} n \right]$$$$Q \uparrow \sum_{n=0}^{N-1} \left[ A_0 \sin \frac{2 \pi k}{N} n \cdot \cos \frac{2 \pi k}{N} n - A_0 \cos \frac{2 \pi k}{N} n \cdot \sin \frac{2 \pi k}{N} n \right]$$

利用恒等式 $\cos A\cos B+\sin A\sin B=\cos (A-B)$ 和 $\sin A\cos B-\cos A\sin B=\sin (A-B)$，

$$I \rightarrow \sum_{n=0}^{N-1} A_0 \cos 0 = A_0 N$$$$Q \uparrow \sum_{n=0}^{N-1} A_0 \sin 0 = 0$$

因此，DFT的输出幅度被证明为 $A_{0}N$。

对于一个实正弦波，$s_Q[n]$ 为0，以上等式中只有部分 $I$ 的第一项保留下来。由于 ${\cos }^{2}A=1/2(1+\cos 2A)$，实正弦波的DFT输出幅度为 $A_{0}N/2$。

考虑到 $s[n]$ 是由两个幅度为1和0.75的实正弦波组成的，我们可以在图1.69b中看到，1kHz的正弦波具有幅度 $1\times N/2=4$，而2kHz的正弦波具有幅度 $0.75\times N/2=3$。

相位

要解读图1.69b的相位图，我们需要回到图1.32，在其中生成一个在时间I轴上的正弦波，我们看到在三维中，两个脉冲分别代表两个复正弦波，位于+F和-F处，并分别被旋转了-90度和+90度。换句话说，相位参考是I轴上的余弦。

因此，图1.69b中频率为1的第一个频段在8000 * 1/8 = 1 kHz处的相位为-90度。根据恒等式$\cos (A-90°)=\sin (A)$，它确实是一个相位为-90度的余弦波。对应的频段-1的相位显然是-(-90°) = +90°。

至于第二项$0.75\sin 2\pi (2/8)n+120°$，它是一个相位偏移为120度的2kHz正弦波，或者是一个相位为-90° + 120° = +30°的余弦波，如图1.69b的频段2所示。

参考图1.68中的时域图，第一个正弦波$s_1(t)$根据其-90度余弦（或0度正弦）相位“定位”在原点周围，而第二个正弦波$s_2(t)$则根据其30度余弦（或120度正弦）相位定位在原点周围。正如之前所分析的，通过相位图，DFT实际上在频率$F_s\cdot k/N$处找到了所有正弦波在时间上的对齐方式。

请记住，图1.69b中的图像——再一次——是重叠的sinc函数。然而，由于信号由两个精确的分析频率组成，频域被采样在零交叉点的精确位置。因此，sinc函数变得不可见，看起来像是两组脉冲。

1.10.3 单位脉冲

在知道矩形信号的DFT后，我们有两种方法可以找到单位脉冲的傅里叶变换。

$$s[n] = \delta[n]$$

时频双重性： 仔细观察DFT和IDFT方程可以发现，正变换和逆变换几乎完全相同，除了缩放因子 $1/N$ 和分析正弦波旋转方向。因此，时间域和频率域是对偶的，时间域信号的DFT可以由频率域信号的IDFT得到。例如，图1.60中的频率bin 0处的单个脉冲在时间域中是一个全为1的矩形序列。反之亦然：时间域中的单个脉冲对应于频率域中的一个全为1的矩形序列。

矩形信号： 从图1.59中可以明显看出，单位脉冲也是一个长度为$L=1$的矩形序列。因此，

$$I \rightarrow S_I[k] = |S[k]| = \frac{\sin \pi k / N}{\sin \pi k / N} = 1$$$$Q \uparrow S_Q[k] = \angle S[k] = 0$$

由于起始样本$n_s=0$，信号是对称的，角度等于0。这个DFT在图1.55的顶部以图形方式说明。

移位单位脉冲

移位单位脉冲的DFT可以从单位脉冲的DFT是一个全为1的序列这一结果中导出。

$$\tilde{s}[n] = \delta[(n + n_0) \mod N]$$

然后，我们利用等式(1.60)：

$$I \rightarrow \tilde{S}_I[k] = \cos\frac{2\pi k}{N}n_0$$$$Q \uparrow \tilde{S}_Q[k] = \sin\frac{2\pi k}{N}n_0 \tag{1.72}$$

这正是图1.56中早先发现的复正弦波。

1.10.4 采样序列

采样序列是一个以周期 $M$ 重复的单位脉冲序列，位于我们的观察窗口内（由于DFT输入的周期性，也在观察窗口外）。图1.70显示了时间域中 $N=15$ 和 $M=3$ 时的采样序列。

​​

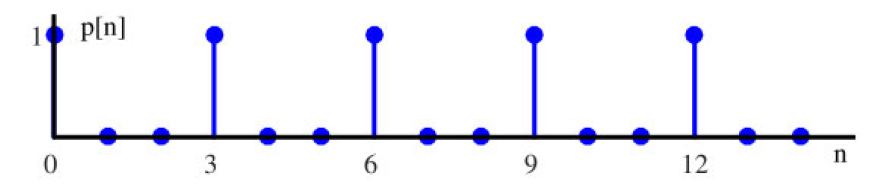
图1.70：时间域中采样序列（$N=15$，$M=3$）

为了计算它的DFT，假设 $p_I[n]=p[n]$ 且 $p_Q[n]=0$。于是，

$$P_I[k] = \sum_{n=0}^{N-1} p[n] \cos\left(2 \pi \frac{k}{N} n\right)$$

由于除了 $n=M$之外，$p[n]=0$，我们可以写成 $p[Mm]=1$，其中 $m=0,1,\cdots ,N/M-1$。我们假设 $N/M$ 为整数，因为否则 $p[n]$ 在观察窗口外将不再是周期性的。因此在上面的例子中，

$$m = 0, 1, 2, 3, 4\ \ \ \ \ \ \ \ n = Mm = 0, 3, 6, 9, 12$$

并且

$$P_I[k] = \sum_{m=0}^{N/M-1} \cos\left(2 \pi \frac{k}{N} Mm\right) = \sum_{m=0}^{N/M-1} \cos\left(2 \pi \frac{k}{N/M} m\right)$$

请注意，上述方程与计算矩形序列的DFT时遇到的等式（1.63）非常相似。在这里，我们有：

$$n_s \rightarrow 0, \quad N \rightarrow \frac{N}{M}, \quad L \rightarrow \frac{N}{M}$$

‍

因此，采样序列的离散傅里叶变换（DFT）可以类似于矩形序列的DFT写为：

$$|P[k]| = \frac{\sin \pi k}{\sin \pi k M/N}$$$$\angle P[k] = 0 \tag{1.73}$$

幅度和相位

序列在图 1.71 中以频域显示，并由 $M$ 个脉冲组成，其中显示了 $M=3$ 和 $N=15$ 的 I 和 Q 分量。尽管由于分子对所有 $k$ 都是 $\pi$ 的倍数，似乎频谱应为零，但我们很快会看到为什么事实并非如此。此外，如上所述，由于序列在时域中关于零是实数且对称的，频域中的相位为零，因此幅度图与 I 分量相同。

​​

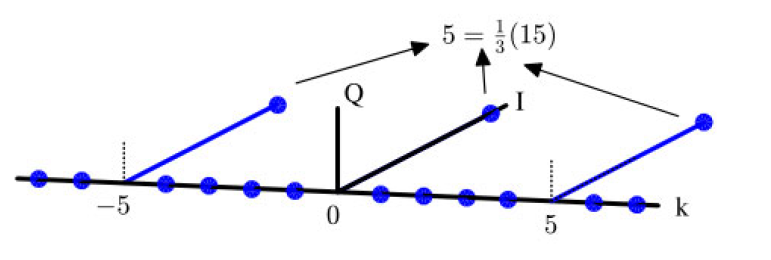
图 1.71: 在频域中采样序列，参数 $N=15$ 和 $M=3$

主瓣峰值

在矩形信号的离散傅里叶变换 (DFT) 中，我们看到当 $k=0$ 时，分子和分母都变为零。在这种情况下，主瓣的峰值等于序列的长度 $L$。我们通过将 $k=0$ 代入 DFT 定义得到了这个值，并推断出结果仅是所有时域样本的和，因为 $\cos (2\pi k/N)=1$ 且 $\sin (2\pi k/N)=0$。在这种情况下，峰值可以很容易地看作是 $N/M$ 个单位脉冲的和，因此等于 $N/M=5$。

请记住在 1.10.2 节中提到的，具有幅度 $A_0$ 的复正弦波在时域中具有 $A_{0}N$ 的幅度，在频域中也是如此。在这里，频谱副本的峰值幅度为 5 而不是 15，这表明由于中间零值样本的影响，实际频谱已缩小了 $1/M=1/3$ 倍。这在图 1.71 中显示。

主瓣位置

这里在频域中有多个脉冲：在一个全为1的矩形序列的DFT中比一个多，但在单位脉冲的DFT中比$N$少。注意从等式(1.73)中可以看出，当分母不为零时，由于整数$k$的存在，频谱显然为零。当分子和分母都为零时，峰值为如上所述的$N/M$。为了找到这些位置，检查分母为零的地方，即为$\pi$的整数倍。

$$\pi k_{\text{peak}} \frac{M}{N} = \text{整数} \cdot \pi$$$$k_{\text{peak}} = \text{整数} \cdot \frac{N}{M}$$

在我们的例子中，由于选定的$N$和$M$值，这些峰值变为0和$\pm 5$，如图1.71所示。在大多数DSP应用中，我们对从$-0.5$到0.5的频率轴感兴趣。在这种情况下，这些位置由$N$归一化，因此由1/M的整数倍给出，即1/3。

如果你猜测这些频域中的脉冲实际上是在峰值和零值处采样的Sinc函数，你是对的（例如，计算一个长度为32的DFT而不是长度为15的序列）。

一个位移采样序列

当上面研究的采样序列被移位一个或多个样本时，会发生什么，如图1.72a所示。我们已经在第1.9节中看到，时间域中信号的移位会使其频谱与一个具有与该移位相等的逆周期的复数正弦信号相乘。随后，我们可以看到，右移1个采样序列的离散傅里叶变换（DFT）可以通过应用公式(1.58)或公式(1.61)得到，即一个采样序列的DFT被旋转了$-2\pi (k/N)$的相位。这在图1.72b中展示，其中相位移可以被表示为：

$$\pm 2\pi \frac{k}{N} n_0 = \pm 2\pi \frac{5}{15} (-1) = \mp 120°$$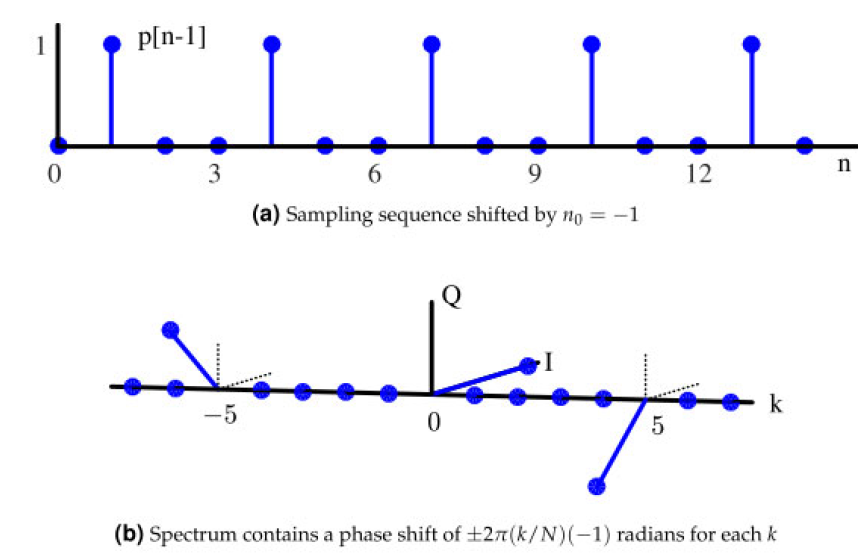

​​

图1.72：在时间域移位的采样序列的频谱包含了相位旋转的脉冲