目录
导入数据
线性模型和主效应模型
线性模型、主效应模型和交互作用模型
使用bandwidth
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ExpSineSquared, WhiteKernel
from sklearn.linear_model import LinearRegression
import causalpy as cp
%config InlineBackend.figure_format = 'retina'导入数据
data = cp.load_data("rd")
data.head()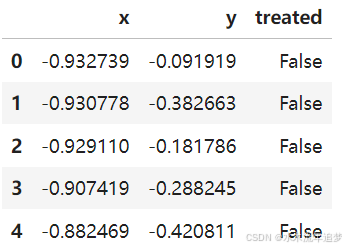
线性模型和主效应模型
result = cp.skl_experiments.RegressionDiscontinuity(
data,
formula="y ~ 1 + x + treated",
model=LinearRegression(),
treatment_threshold=0.5,
)
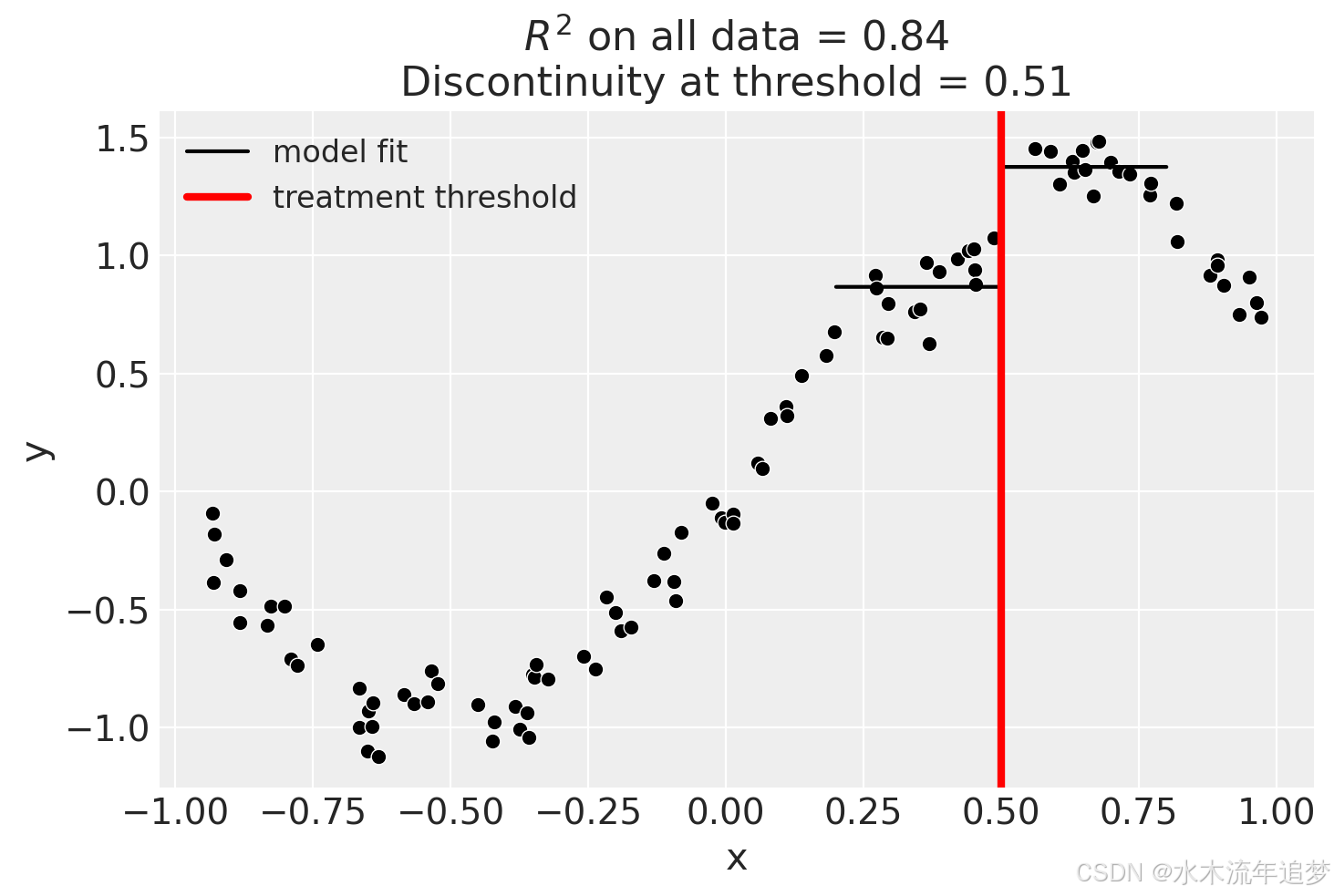
fig, ax = result.plot()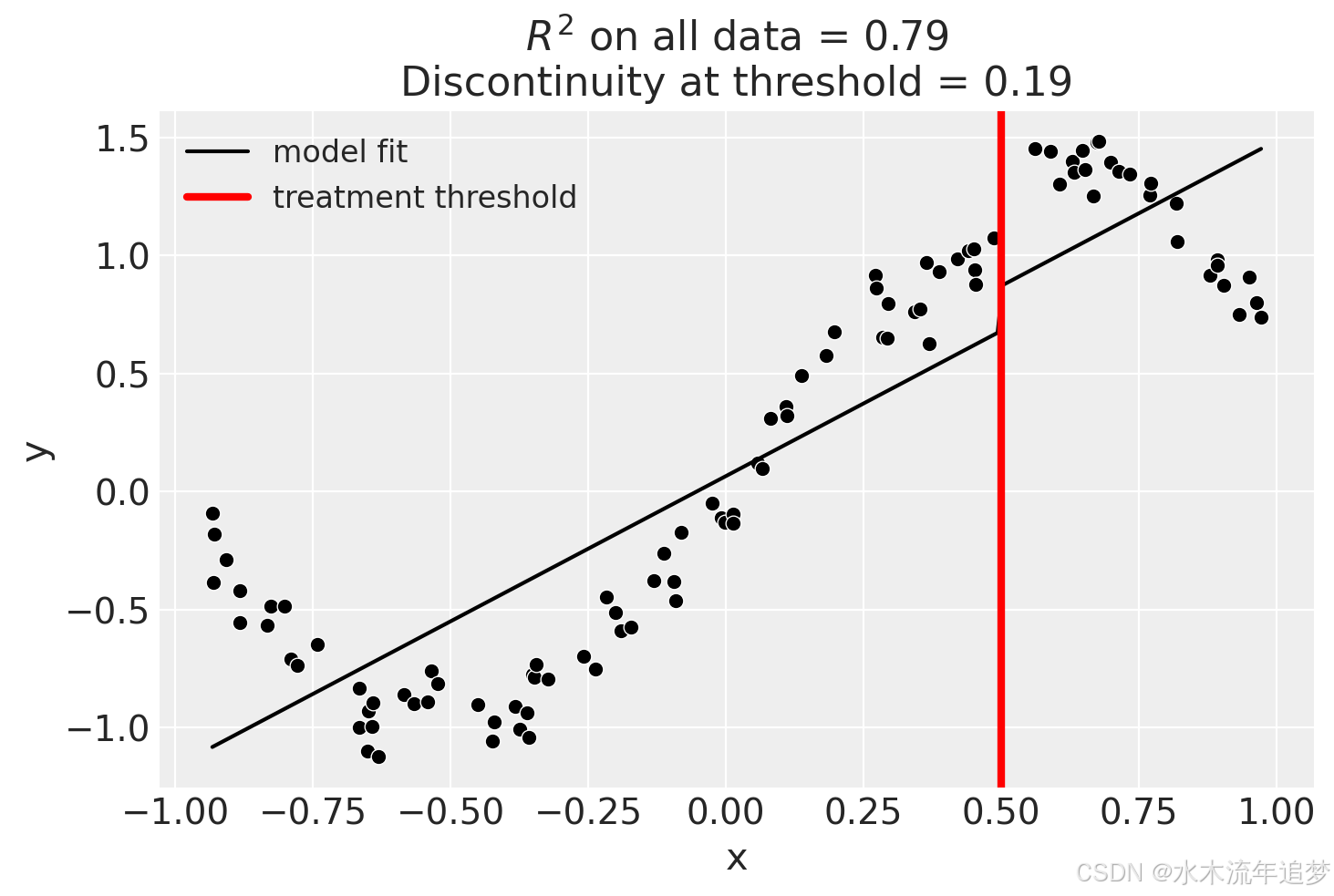
result.summary(round_to=3)Difference in Differences experiment Formula: y ~ 1 + x + treated Running variable: x Threshold on running variable: 0.5 Results: Discontinuity at threshold = 0.19 Model coefficients: Intercept 0 treated[T.True] 0.19 x 1.23
线性模型、主效应模型和交互作用模型
result = cp.skl_experiments.RegressionDiscontinuity(
data,
formula="y ~ 1 + x + treated + x:treated",
model=LinearRegression(),
treatment_threshold=0.5,
)
result.plot();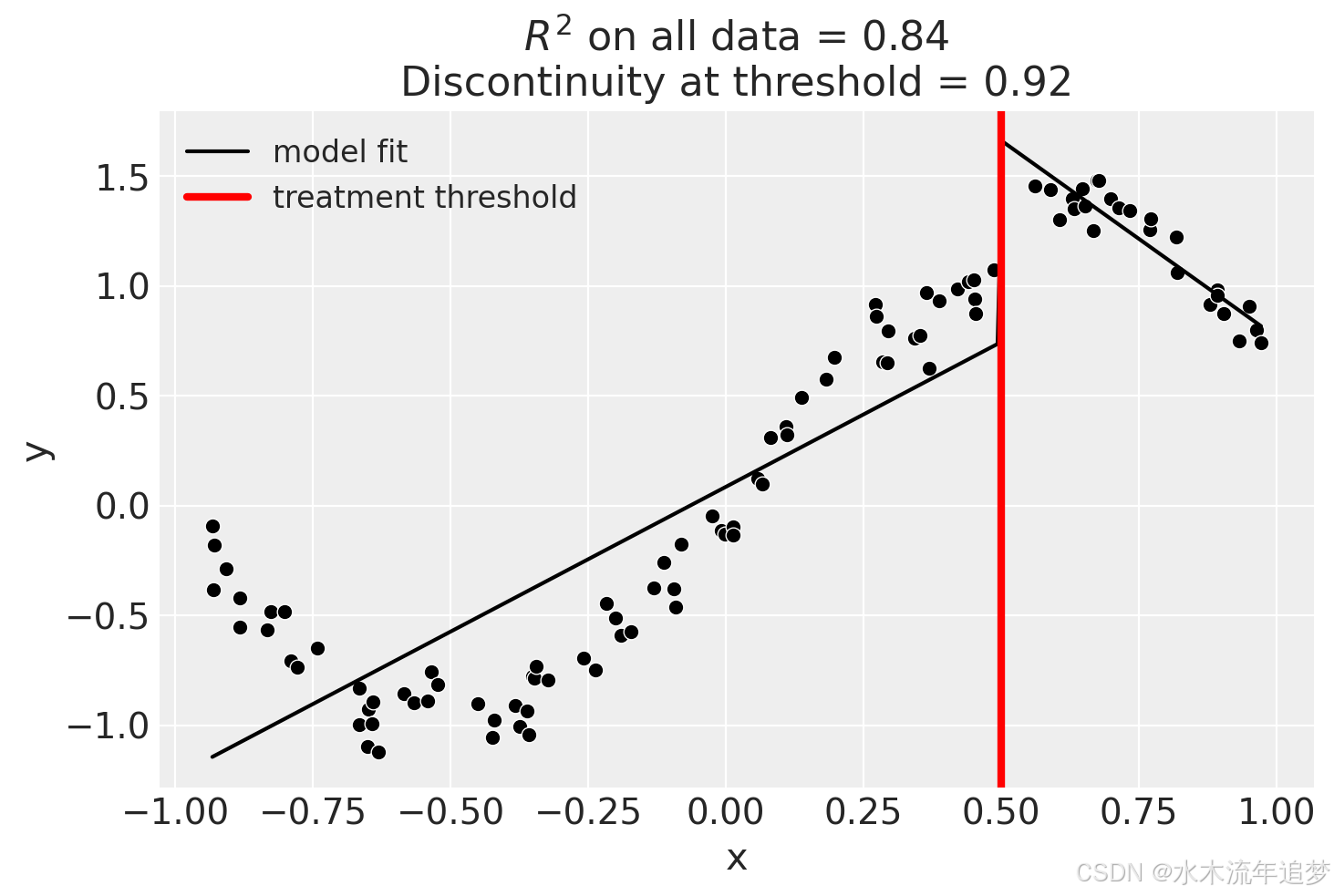
虽然我们可以看到这样做并不能很好地拟合数据,几乎肯定高估了阈值处的不连续性。
result.summary(round_to=3)Difference in Differences experiment Formula: y ~ 1 + x + treated + x:treated Running variable: x Threshold on running variable: 0.5 Results: Discontinuity at threshold = 0.92 Model coefficients: Intercept 0 treated[T.True] 2.47 x 1.32 x:treated[T.True] -3.11
使用bandwidth
我们处理这个问题的一种方法是使用 `bandwidth` 参数。这将只对阈值附近的一定带宽内的数据进行拟合。如果 x 是连续变量,那么模型将只对满足 的数据进行拟合。
result = cp.skl_experiments.RegressionDiscontinuity(
data,
formula="y ~ 1 + x + treated + x:treated",
model=LinearRegression(),
treatment_threshold=0.5,
bandwidth=0.3,
)
result.plot();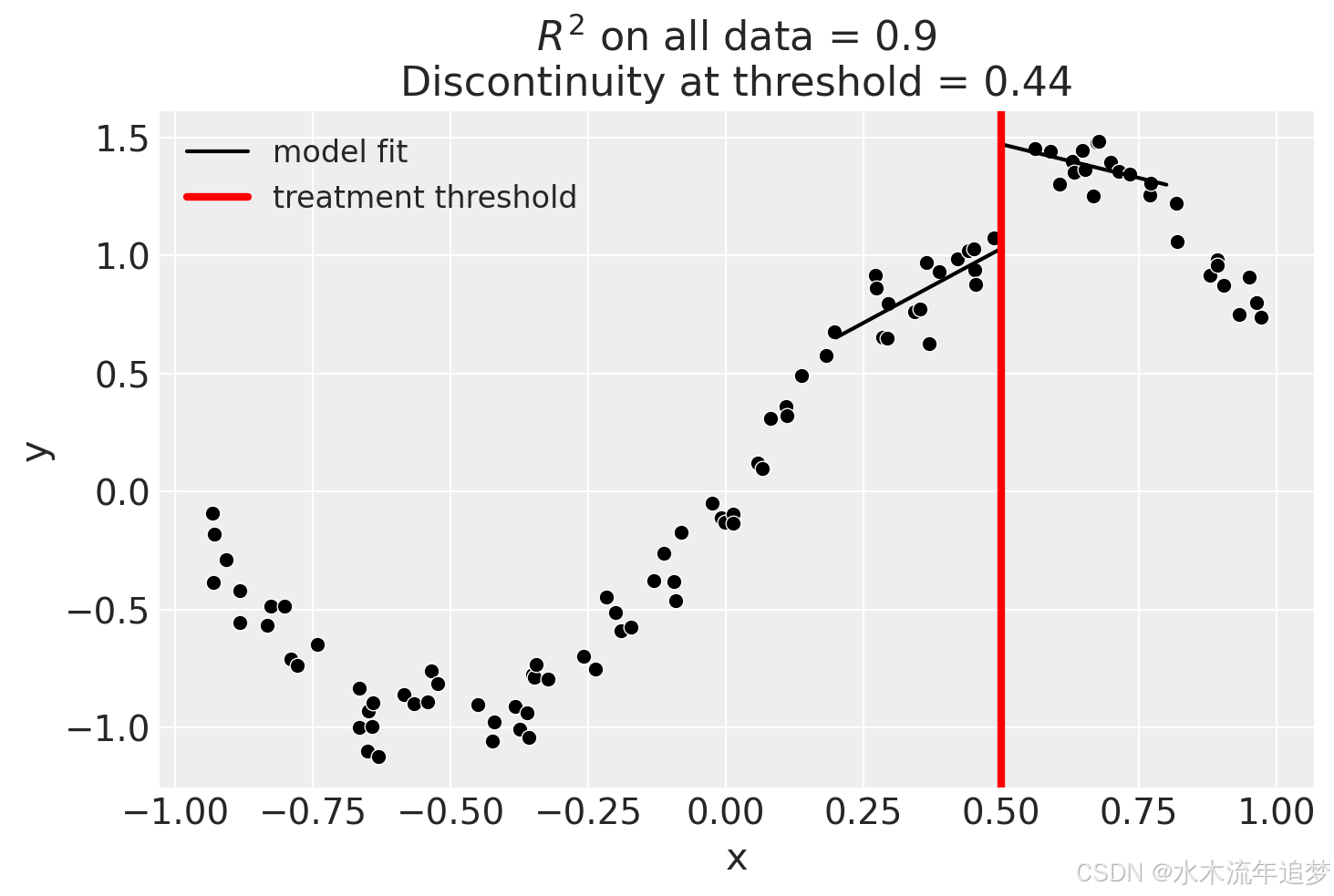
我们甚至可以走得更远,只为接近阈值的数据拟合截距。但很明显,这将涉及更多的估计误差,因为我们使用的数据较少。
result = cp.skl_experiments.RegressionDiscontinuity(
data,
formula="y ~ 1 + treated",
model=LinearRegression(),
treatment_threshold=0.5,
bandwidth=0.3,
)
result.plot();