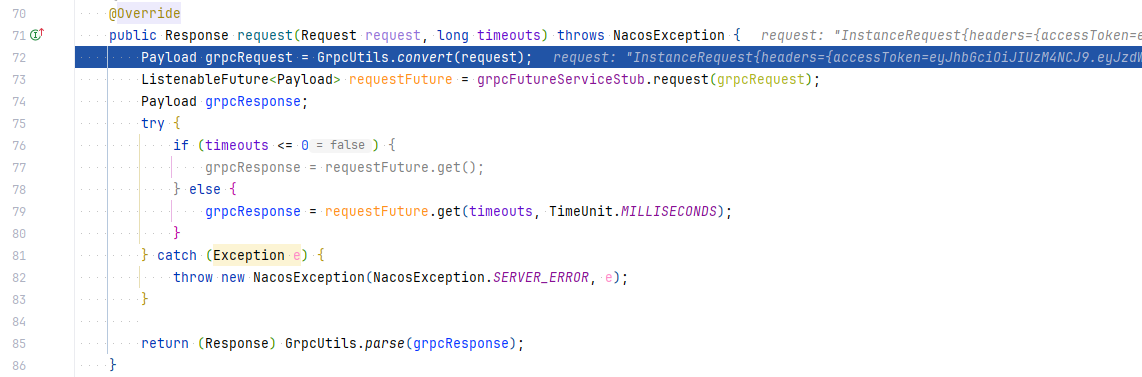
二分图，把所有点划分到两边去，使得所有边都是在集合之间的，集合内部没有边。

一个图是二分图，当且仅当图中不含奇数环(环的边数是奇数)。这是个充分必要条件，是二分图就一定不含奇数环；不含奇数环就一定是二分图。

从前往后遍历每一个点，然后如果当前这个点还没有分好组的话，我们就把它分到左边去(右边也行)，分完这个点之后，遍历一下这个点所有的邻点，所有和这个点连通的点，染色这个点所在的连通块。这个点属于左边的，那他相邻的点就属于右边，和右边这个点相邻的点就属于左边。

可以看成是一个染色的过程，我们要把所有点染上颜色(白色、黑色)。一条边的两个端点颜色不同，属于不同集合。通过这种方式可以把图中所有的点染色。

一个连通块中只要有一个点的颜色确定了，整个连通块所有点的颜色就确定了。

我们就可以用这样一种构造方式把整个图分成两个点集，使得所有边都是出现在两个点集之间的，那么显然是一个二分图。

某一次我们一个白色的点，搜到了一个已经染过颜色的点，之前染过颜色这个点和当前这个点颜色是相同的，那就矛盾了，环中的点一定是奇数。

染色法判断一个图是不是二分图。一个图在染色过程中出现了矛盾，说明存在奇数环，就不是二分图。没有出现矛盾，可以完美的染一遍，就说明没有奇数环，就是二分图。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=1e5+10,M=2e5+10;//无向图两条边2e5

int n,m;
int h[N],e[M],ne[M],idx;
int color[N];//0代表没染色，染色的两种颜色是1和2

void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;    
}

bool dfs(int u,int c){
    color[u]=c;//染色当前点
    
    for(int i=h[u];i!=-1;i=ne[i]){//遍历这的点所有出边
        int j=e[i];
        if(!color[j]){//如果没有染色
            if(!dfs(j,3-c)) return false;//那就染色，3-c把1变成2，把2变成1，染相对的颜色。
        }else if(color[j]==c) return false;//如果已经染色，两个相邻点颜色相同，那就矛盾了(染色图一条边的两段颜色不同)，说明存在奇数环。
    }
    return true;
}

int main(){
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }
    
    bool flag=true;//是否成功完成染色过程
    for(int i=1;i<=n;i++){
        if(!color[i]){
            if(!dfs(i,1)){//染了颜色1
                flag=false;
                break;
            }
        }
    }
    
    if(flag) puts("Yes");
    else puts("No");
    return 0;
}