一文讲解多种GIS分析功能

GIS行业有很多分析功能，对于刚入行的新手有着足够的吸引力，其实有许多分析功能实现原理大差不差，比如模型压平，基于模型的淹没分析以及模型裁切。本文将以模型裁切为切入口进行介绍其中原理。

首先

（立方体剖切示意图，图源：Mapmost SDK for WebGL）

在GIS行业中，诸多分析功能吸引着新手探索，而其中不乏原理相通之处，诸如模型压平、淹没分析与模型裁切等。以模型裁切为例，其核心在于利用空间分析技术，从复杂的地理实体中依据预定条件精准提取或裁切所需部分。这一过程涉及空间叠加运算，即确定数据集之间的空间关系，通过设定裁切边界来筛选目标区域，剔除非关注部分。相似地，模型压平是将局部模型扁平化，淹没分析预测水体上涨影响范围，皆围绕空间筛选与关系处理展开，虽应用场景各异，但均依托于GIS强大的空间分析引擎实现高效数据挖掘与可视化。对这些原理的掌握，将为GIS新手打下坚实基础。

通过剖析立方体剖切原理，本指南将启发现学者触类旁通，灵活运用此基础技法拓展至其他两项GIS分析功能实现，深入浅出解析空间分析精髓。

功能步骤拆解：

判定像素在立方体之内
在立方体之内则丢弃像素，否则正常渲染

对于第2点，glsl中提供了discard功能，用于丢弃当前像素。那么问题就只剩一个了，如何判定像素在立方体之内？

在OpenGL Shading Language (GLSL)中，准确判定像素是否位于立方体内部是一个涉及空间坐标变换与逻辑判断的关键过程。具体实现步骤可细分为下面两个步骤：

一、坐标空间统一

首先，需要保证像素坐标与立方体顶点坐标处于同一个坐标系中，个人推荐是在模型本地坐标系下进行。这里简单回顾下MVP矩阵转换。MVP矩阵分别是模型（Model）、观察（View）、投影（Projection）三个矩阵。

首先

（立方体剖切示意图，图源：Mapmost SDK for WebGL）

通过剖析立方体剖切原理，本指南将启发现学者触类旁通，灵活运用此基础技法拓展至其他两项GIS分析功能实现，深入浅出解析空间分析精髓。

功能步骤拆解：

判定像素在立方体之内
在立方体之内则丢弃像素，否则正常渲染

对于第2点，glsl中提供了discard功能，用于丢弃当前像素。那么问题就只剩一个了，如何判定像素在立方体之内？

一、坐标空间统一

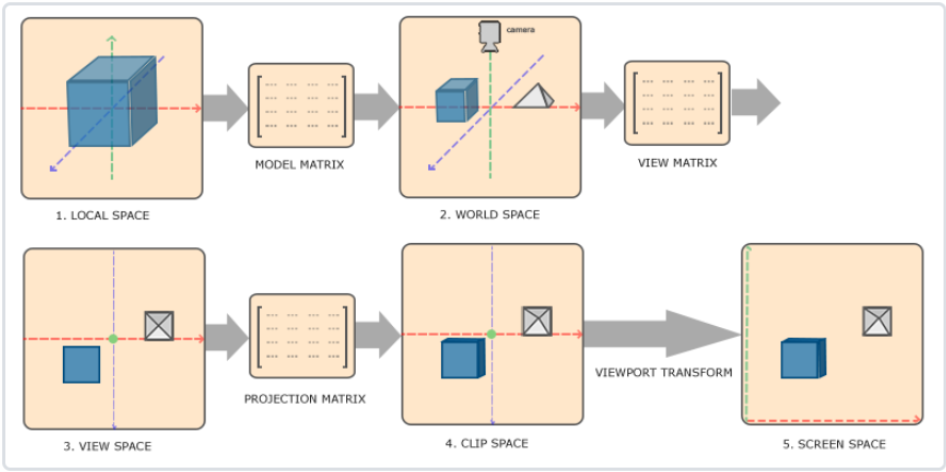
（MVP矩阵流程图，图源：https://blog.csdn.net/s178435865/article/details/131706248）

通常引擎中的片元着色器中都会有模型本地坐标系下的变量，形似：v_PositionMC，以及模型矩阵：u_ModelMatrix，因为需要把立方体中心点（世界坐标系）坐标转到模型本地坐标系下，实际上我们用到的是模型矩阵的逆矩阵，在验证技术链路时建议使用下面逆矩阵运算方法，验证通过后建议由JS提前运算，使用uniform参数传入，避免GPU计算资源浪费，因为JS计算只需要计算一次，片元计算是每一帧每一个像素都要调用下面方法，会造成计算资源浪费，下面是着色器代码进行矩阵逆运算方法：

mat4 inverse_mat4(mat4 m)
{
    float Coef00 = m[2][2] * m[3][3] - m[3][2] * m[2][3];
    float Coef02 = m[1][2] * m[3][3] - m[3][2] * m[1][3];
    float Coef03 = m[1][2] * m[2][3] - m[2][2] * m[1][3];
    
    float Coef04 = m[2][1] * m[3][3] - m[3][1] * m[2][3];
    float Coef06 = m[1][1] * m[3][3] - m[3][1] * m[1][3];
    float Coef07 = m[1][1] * m[2][3] - m[2][1] * m[1][3];
    
    float Coef08 = m[2][1] * m[3][2] - m[3][1] * m[2][2];
    float Coef10 = m[1][1] * m[3][2] - m[3][1] * m[1][2];
    float Coef11 = m[1][1] * m[2][2] - m[2][1] * m[1][2];
    
    float Coef12 = m[2][0] * m[3][3] - m[3][0] * m[2][3];
    float Coef14 = m[1][0] * m[3][3] - m[3][0] * m[1][3];
    float Coef15 = m[1][0] * m[2][3] - m[2][0] * m[1][3];
    
    float Coef16 = m[2][0] * m[3][2] - m[3][0] * m[2][2];
    float Coef18 = m[1][0] * m[3][2] - m[3][0] * m[1][2];
    float Coef19 = m[1][0] * m[2][2] - m[2][0] * m[1][2];
    
    float Coef20 = m[2][0] * m[3][1] - m[3][0] * m[2][1];
    float Coef22 = m[1][0] * m[3][1] - m[3][0] * m[1][1];
    float Coef23 = m[1][0] * m[2][1] - m[2][0] * m[1][1];
    
    const vec4 SignA = vec4( 1.0, -1.0,  1.0, -1.0);
    const vec4 SignB = vec4(-1.0,  1.0, -1.0,  1.0);
    
    vec4 Fac0 = vec4(Coef00, Coef00, Coef02, Coef03);
    vec4 Fac1 = vec4(Coef04, Coef04, Coef06, Coef07);
    vec4 Fac2 = vec4(Coef08, Coef08, Coef10, Coef11);
    vec4 Fac3 = vec4(Coef12, Coef12, Coef14, Coef15);
    vec4 Fac4 = vec4(Coef16, Coef16, Coef18, Coef19);
    vec4 Fac5 = vec4(Coef20, Coef20, Coef22, Coef23);
    
    vec4 Vec0 = vec4(m[1][0], m[0][0], m[0][0], m[0][0]);
    vec4 Vec1 = vec4(m[1][1], m[0][1], m[0][1], m[0][1]);
    vec4 Vec2 = vec4(m[1][2], m[0][2], m[0][2], m[0][2]);
    vec4 Vec3 = vec4(m[1][3], m[0][3], m[0][3], m[0][3]);
    
    vec4 Inv0 = SignA * (Vec1 * Fac0 - Vec2 * Fac1 + Vec3 * Fac2);
    vec4 Inv1 = SignB * (Vec0 * Fac0 - Vec2 * Fac3 + Vec3 * Fac4);
    vec4 Inv2 = SignA * (Vec0 * Fac1 - Vec1 * Fac3 + Vec3 * Fac5);
    vec4 Inv3 = SignB * (Vec0 * Fac2 - Vec1 * Fac4 + Vec2 * Fac5);
    
    mat4 Inverse = mat4(Inv0, Inv1, Inv2, Inv3);
    
    vec4 Row0 = vec4(Inverse[0][0], Inverse[1][0], Inverse[2][0], Inverse[3][0]);
    
    float Determinant = dot(m[0], Row0);
    
    Inverse /= Determinant;
    
    return Inverse;
}

二、立方体边界检验

通过两个变量定义立方体：中心点（u_center）以及长宽高尺寸(u_size)，

通过把模型本地坐标减去立方体中心点坐标得到相对坐标，然后使用相对坐标对比立方体尺寸，如果相对坐标XYZ各自分量的绝对值都小于立方体尺寸，则判定像素是否在立方体之内，否则判定为立方体之外，伪代码如下：

// 模型本地坐标
varying vec3 v_PositionMC;
uniform mat4 u_ModelMatrix;
// 世界坐标系下的立方体中心坐标
uniform vec3 u_centerWC;
// 立方体尺寸
uniform vec3 u_size;
mat4 inverse_mat4(mat4 m)
{
    ...
    ...
}
void main() {
    vec3 centerMC = vec3(inverse_mat4(u_ModelMatrix) * vec4(u_centerWC, 1.0));
    vec3 offsetMC = v_PositionMC - centerMC;
    if (abs(offsetMC.x) <= u_size.x && abs(offsetMC.y) <= u_size.y && abs(offsetMC.z) <= u_size.z) {
        discard
    }
}

以上立方体剖切大致实现流程，在此基础上可以对立方体进行旋转，这时模型顶点也要做相应的旋转。当然了在GIS行业中，通常是使用geojson文件的不规则平面数据进行裁剪与压平等分析，这里给出思路：