数学建模笔记——层次分析法

层次分析法（ Analytic Hierarchy Process，简称 AHP）是对一些较为复杂、较为模糊的问题作出决策的简易方法，它特别适用于那些难于完全定量分析的问题。

1. 层次分析法的基本原理和步骤

人们在进行社会的、经济的以及科学管理领域问题的系统分析中，面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。

运用层次分析法建模，大体上可按下面四个步骤进行：

1. 建立递阶层次结构模型；
2. 构造出各层次中的所有判断矩阵；
3. 层次单排序及一致性检验；
4. 层次总排序及一致性检验。

下面说明这四个步骤的实现过程

2. 层次分析法的建模过程

2.1 问题的提出

新浪微博要选出一个明星作为微博之星，现在有三个候选明星A、B、C,该选择哪位明星呢？
考虑一个明星的成就可以看其粉丝数、颜值、作品数量、作品质量(考虑用作品某瓣平均评分代替)
A、B、C的相关数据如下

表 1 明星成就表

明星	粉丝数	颜值	作品质量	作品数量
A	6000w	10	6.5	25
B	3400w	6	8.1	46
C	5500w	8	7.5	31

2.2 模型原理

应用 AHP分析决策问题时，首先要把问题条理化、层次化，构造出一个有层次的结构模型。在这个模型下，复杂问题被分解为元素的组成部分。这些元素又按其属性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。这些层次可以分为三类：

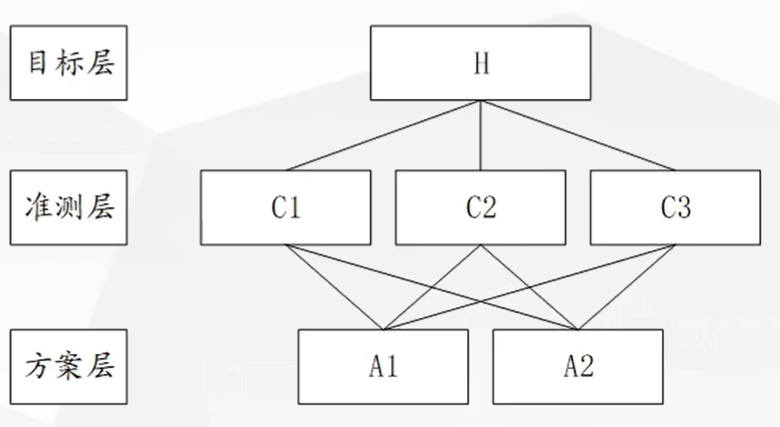
1. 最高层：这一层次中只有一个元素，一般它是分析问题的预定目标或理想结果，因此也称为目标层。
2. 中间层：这一层次中包含了为实现目标所涉及的中间环节，它可以由若干个层次组成，包括所需考虑的准则、子准则，因此也称为准则层。
3. 最底层：这一层次包括了为实现目标可供选择的各种措施、决策方案等，因此也称为措施层或方案层。

递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关，一般地层次数不受限制。每一层次中各元素所支配的元素一般不要超过 9 个。这是因为支配的元素过多会给两两比较判断带来困难。

图 1 层次结构模型

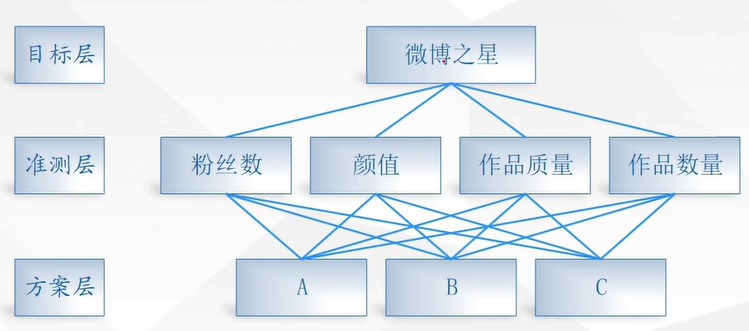
2.3 为该问题建立层次结构模型

建立的递阶层次结构模型如下

图 2 建立递阶层次结构模型

2.4 构造判断矩阵

1. 判断矩阵的含义

• 对指标的重要性进行两两比较，构造判断矩阵，从而科学求出权重
• 矩阵中元素$a_{ij}$的意义是，第$i$个指标相对第$j$个指标的重要程度

定义 1 若矩阵$A=(a_{i}j{)}_{n\times n}$满足

• $a_{ij}>0$
• $a_{ji}=\frac{1}{a_{ij}}$($i,j=1,2,\cdots ,n$)

则称之为正互反矩阵(易见$a_{ii}=1,i=1,\cdots ,n$ )。

关于如何确定$a_{ij}$ 的值，Saaty 等建议引用数字 1~9 及其倒数作为标度。表 7- 1 列出了 1~9 标度的含义：

表 2 标度的含义

标度	含义
1	表示两个因素相比 具有相同重要性
3	表示两个因素相比，前者比后者稍重要
5	表示两个因素相比，前者比后者明显重要
7	表示两个因素相比，前者比后者强烈重要
9	表示两个因素相比，前者比后者极端重要
2, 4, 6, 8	表示上述判断的中间值
倒数	若因素 i 与因素 j 的重要性之比为 $a_{ij}$，那么因素 j 与因素 i 的重要性之比为 $a_{ji}=1/a_{ij}$

2. 为该问题构造判断矩阵

依次对矩阵进行两两比较，得到完整的判断矩阵，如表3所示

表 3 判断矩阵

	粉丝数	颜值	作品质量	作品数量
粉丝数	1	2	3	5
颜值	1/2	1	1/2	2
作品质量	1/3	2	1	1/2
作品数量	1/5	1/2	2	1

由于两两比较的过程中忽略了其他因素，最后导致最后结果可能出现矛盾

$a_{23}=\frac{1}{2}$说明作品质量比颜值重要

$a_{24}=2$说明颜值比作品数量重要

由上面两个结果可以推出作品质量比作品数量重要

而由$a_{34}=\frac{1}{2}$推出作品数量比作品质量重要，产生了矛盾

因此我们需要进行一致性检验避免上述情况

2.5 一致性检验

1. 一致性检验方法

判断矩阵$A$对应于最大特征值${\lambda }_{\max }$的特征向量$W$ ,经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值，这一过程称为层次单排序。
上述构造成对比较判断矩阵的办法虽能减少其它因素的干扰，较客观地反映出一对因子影响力的差别。但综合全部比较结果时，其中难免包含一定程度的非一致性。如果比较结果是前后完全一致的，则矩阵$A$的元素还应当满足：
$$a_{ij}{a}_{jk}=a_{ik},\forall i,j,k=1,2,\cdots n$$
定义 2 满足上述关系式的正互反矩阵称为一致矩阵。

需要检验构造出来的(正互反)判断矩阵$A$是否严重地非一致，以便确定是否接受$A$。
定理 1 正互反矩阵$A$的最大特征根${\lambda }_{\max }$必为正实数，其对应特征向量的所有分量均为正实数。$A$的其余特征值的模均严格小于${\lambda }_{\max }$ 。
定理 2 若$A$为一致矩阵，则

1. $A$必为正互反矩阵。
2. $A$的转置矩阵$A^T$也是一致矩阵。
3. $A$ 的任意两行成比例，比例因子大于零，从而$\mathrm{rank}(A)=1$(同样，$A$ 的任意两列也成比例)。
4. $A$的最大特征值${\lambda }_{\max }=n$ ,其中$n$为矩阵$A$的阶。$A$的其余特征根均为零。
5. 若$A$的最大特征值 ${\lambda }_{\max }$ 对应的特征向量为$W=(w_1,\cdots ,w_n{)}^T$,则$a_{ij}=\frac{w_i}{w_j}$,$\forall i,j=1,2,\cdots ,n$,即

$$A=\left[\begin{array}{cccc}\frac{w_1}{w_1}& \frac{w_1}{w_2}& \cdots & \frac{w_1}{w_n}\\ \frac{w_2}{w_1}& \frac{w_2}{w_2}& \cdots & \frac{w_2}{w_n}\\ \cdots & \cdots & \cdots & \cdots \\ \frac{w_n}{w_1}& \frac{w_n}{w_2}& \cdots & \frac{w_n}{w_n}\end{array}\right]$$

定理 3 $n$阶正互反矩阵$A$为一致矩阵当且仅当其最大特征根${\lambda }_{\max }=n$ ,且当正互反矩阵$A$非一致时，必有${\lambda }_{\max }>n$ 。

根据定理 3,我们可以由${\lambda }_{\max }$是否等于$n$来检验判断矩阵$A$是否为一致矩阵。由于特征根连续地依赖于$a_{ij}$,故${\lambda }_{\max }$比$n$ 大得越多，$A$的非一致性程度也就越严重，${\lambda }_{\max }$对应的标准化特征向量也就越不能真实地反映出 X = { x 1 , ⋅ ⋅ ⋅ , x n } X=\{x_1,\cdotp\cdotp\cdotp,x_n\} X={x1​,⋅⋅⋅,xn​}在对因素$Z$的影响中所占的比重。因此，对决策者提供的判断矩阵有必要作一次一致性检验，以决定是否能接受它。

对判断矩阵的一致性检验的步骤如下：

1. 计算一致性指标$CI$
   $$CI=\frac{{\lambda }_{\max }-n}{n-1}$$

2. 查找相应的平均随机一致性指标$RI$ 。对 $n=1,\cdots ,9$ ,Saaty 给出了$RI$ 的值如表 3所示。

表 4

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45

$RI$的值是这样得到的，用随机方法构造 500 个样本矩阵：随机地从 1~9 及其倒数中抽取数字构造正互反矩阵，求得最大特征根的平均值${\lambda }_{\max }^{\prime }$,并定义
$$RI=\frac{{\lambda }_{\max }^{\prime }-n}{n-1}$$

3. 计算一致性比例$CR$
   $$CR=\frac{CI}{RI}$$

$$CR=\frac{CI}{RI}\{\begin{array}{llc}& 0,& \text{判断矩阵为一致矩阵}\\ & <0.1,& \text{判断矩阵一致}\\ & \ge 0.1,& \text{判断矩阵不一致}\end{array}$$

2. 对上述判断矩阵进行一致性检验

当前判断矩阵的${\lambda }_{max}=4.68,n=4$, 求得$CI=0.227$, 查表$RI=0.89$, 得CR = 0. 255，CR$\geq$0.1需修改判断矩阵。

修改后的判断矩阵如表5

表 5 修改后的判断矩阵

	粉丝数	颜值	作品质量	作品数量
粉丝数	1	2	3	5
颜值	1/2	1	1/2	2
作品质量	1/3	2	1	2
作品数量	1/5	1/2	1/3	1

对修改后的判断矩阵进行一致性检验，求得${\lambda }_{max}=4.1128,n=4$, 求得$CI=0.227$, 查表$RI=0.89$, 得CR = 0.0418，CR$\textless$0.1，通过一致性检验

2.6 求权重

1.算术平均法求权重

一般步骤：

1. 将判断矩阵按照列归一化（每个元素除以其所在列的和）
2. 将归一化的各列相加（按行求和）
3. 将相加后得到的向量中每个元素除以n即可得到权重向量

假设判断矩阵$A=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right]$，那么算术平均法求得的权重向量
$$w_i=\frac{1}{n}\sum _{j=1}^n\frac{a_{ij}}{{\sum }_{k=1}^n{a}_{kj}}(i=1,2,3,...,n)$$
由算术平均法求出微博之星的权重：

由表5的判断矩阵，进行列归一化得

表 6 进行归一化后的判断矩阵

	粉丝数	颜值	作品质量	作品数量
粉丝数	0.492	0.364	0.600	0.500
颜值	0.246	0.182	0.100	0.200
作品质量	0.164	0.364	0.200	0.200
作品数量	0.098	0.091	0.100	0.100

进行算术平均后求得权重

	权重
粉丝数	0.489
颜值	0.182
作品质量	0.232
作品数量	0.097

2. 几何平均法求权重

一般步骤：

1. 将判断矩阵的元素按照行相乘得到一个新的列向量
2. 将新的向量的每个分量开n次方
3. 对该列向量进行归一化即可得到权重向量

假设判断矩阵A=$\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{n1}& \cdots & a_{nn}\end{array}\right]$

那 么 算 术 平 均 法 求 得 的 权 重 向 量
$$w_i=\frac{{\left({\prod }_{j=1}^n{a}_{ij}\right)}^{\frac{1}{n}}}{{\sum }_{k=1}^n{\left({\prod }_{i=1}^n{a}_{kj}\right)}^{\frac{1}{n}}},(i=1,2,\dots ,n)$$
用几何平均法求微博之星的权重：

由表5的判断矩阵，行相乘后开方，得

	行相乘后开方
粉丝数	2.34
颜值	0.84
作品质量	1.07
作品数量	0.47

求出权重

	权重
粉丝数	0.495
颜值	0.178
作品质量	0.227
作品数量	0.100

3. 特征值法求权重

一致矩阵有一个特征值n，其余特征值为0，同时我们很容易得到特征值为n时，对应的特征向量刚好为
$$k{\left[\frac{1}{a_{11}},\frac{1}{a_{12}},\dots ,\frac{1}{a_{1n}}\right]}^T(k\ne 0)$$
假如我们的判断矩阵一致性可以接受，我们可以仿照一致性矩阵权重的求法

1. 求出矩阵A的最大特征值以及其对应的特征向量
2. 对求出的特征向量进行归一化即可得到我们的权重

由表5的判断矩阵，求出特征向量如下

	特征向量
粉丝数	0.8487
颜值	0.3076
作品质量	0.3962
作品数量	0.1676

求出权重

	权重
粉丝数	0.493
颜值	0.179
作品质量	0.230
作品数量	0.097

2.7 求评分

3种方法的权重差不多，我们选用特征值法，结果如下

明星	粉丝数	颜值	作品质量	作品数量	评分
A	0.40*0.493	0.42*0.179	0.29*0.23	0.25*0.097	0.363
B	0.23*0.493	0.25*0.179	0.37*0.23	0.45*0.097	0.287
C	0.37*0.493	0.33*0.179	0.34*0.23	0.30*0.097	0.349

由上可知，应当选A当选微博之星

3. 层次分析法的python实现代码

3.1 一致性检验代码

import numpy as np
# A为判断矩阵
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2],
             [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
n = A.shape[0]  # 获取A的行数

# 求出最大特征值和对应的特征向量，np.linalg.eig()函数可以求出矩阵的特征值和特征向量
eigvals, eigvecs = np.linalg.eig(A)
max_eigval = max(eigvals)  # 最大特征值
CI = (max_eigval-n)/(n-1)  # 一致性指标
RI = [0, 0.0001, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41,
      1.46, 1.49, 1.52, 1.54, 1, 56, 1, 58, 1.59]  # 随机一致性指标
# 上述n=2时，一定是一致矩阵，为了避免分母为0，将第二个元素改为很接近0的正数
CR = CI/RI[n-1]  # 一致性比例
print("一致性指标CI=", CI)
print("一致性比例CR=", CR)
if CR < 0.1:
    print("一致性较好,判断矩阵可以接受")
else:
    print("一致性较差，判断矩阵不可接受")

输出：

一致性指标CI= (0.037610012730716846+0j)
一致性比例CR= (0.04225844127046837+0j)
一致性较好,判断矩阵可以接受

3.2 求权重代码

1. 算术平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2],
             [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 计算每一列的和
Asum = np.sum(A, axis=0)
# 获取A的行数
n = A.shape[0]
# 归一化，二维数组除以一维数组，会自动将一维数组扩展为二维数组，然后再相除
Stand_A = A/Asum
# 各列相加到同一行
A_sum_row = np.sum(Stand_A, axis=1)
# 求出权重
weight = A_sum_row/n
print("权重为：", weight)

输出:

权重为： [0.48885991 0.18192996 0.2318927  0.09731744]

2. 几何平均法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2],
             [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 将A中的每一行元素相乘得到一列向量
# np.prod()函数可以计算数组中所有元素的乘积
prod_A = np.prod(A, axis=1)
# 将新的向量的每个分量开n次方等价于求n次方根
prod_n_A = np.power(prod_A, 1/4)
# 归一化处理
re_prod_A = prod_n_A/np.sum(prod_n_A)
# 输出特征向量
print("特征向量为：", re_prod_A)

输出：

特征向量为： [0.49492567 0.17782883 0.22724501 0.1000005 ]

3. 特征值法求权重

import numpy as np
# 定义判断矩阵A
A = np.array([[1, 2, 3, 5], [1/2, 1, 1/2, 2],
             [1/3, 2, 1, 2], [1/5, 1/2, 1/2, 1]])
# 获取A的行数
n = A.shape[0]
# 求出特征值和特征向量
eigvals, eigvecs = np.linalg.eig(A)
# 找出最大特征值的索引，np.argmax()函数可以找出数组中最大值的索引
max_index = np.argmax(eigvals)
# 找出最大特征值对应的特征向量
max_eigvec = eigvecs[:, max_index]
# 归一化处理
weight = max_eigvec/np.sum(max_eigvec)
print("权重为：", weight)

输出：

权重为： [0.4933895 +0.j 0.17884562+0.j 0.230339  +0.j 0.09742588+0.j]