【线性代数】正定矩阵，二次型函数

news2024/12/25 9:23:17

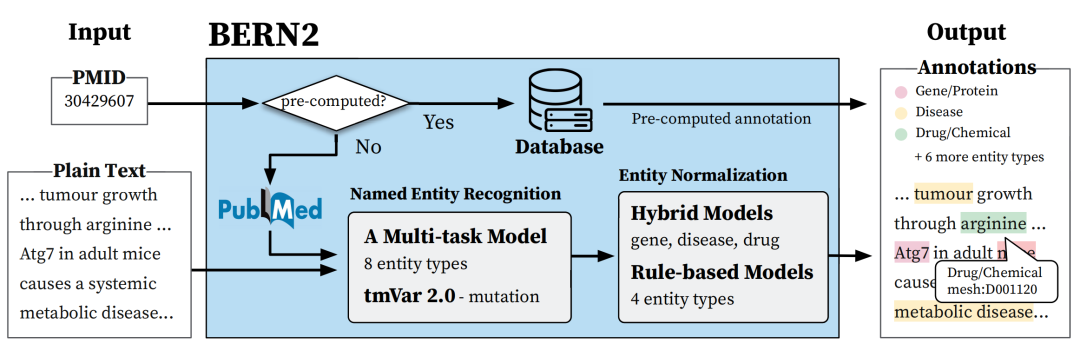
本文主要介绍正定矩阵，二次型函数，及其相关的解析证明过程和各个过程的可视化几何解释（深蓝色字体）。

非常喜欢清华大学张颢老师说过的一段话：如果你不能用可视化的方式看到事情的结果，那么你就很难对这个事情有认知，认知就是直觉，解析的东西可以让你理解，但未必能让你形成直觉，因为他太反直觉了。

正定矩阵

定义

给定一个大小为 n×n 的实对称矩阵 A ，若对于任意长度为 n 的非零向量 $X$ ，有 $X^{T}AX>0$ 恒成立，则矩阵 A是一个正定矩阵。

推荐文章：如何理解正定矩阵和半正定矩阵 - marsggbo - 博客园 (cnblogs.com)

正定矩阵有什么用

给定一个多元二次函数： $f(x)=(x_{1}-x_{2})^{2}+2x_{1}+x_{2}+3$

写成矩阵的形式： $f(x)=\begin{bmatrix} x_{1} & x_{2} \end{bmatrix}\begin{bmatrix} 1 &-1 \\-1 &1 \end{bmatrix}\begin{bmatrix} x_{1}\\ x^{_{2}} \end{bmatrix}+\begin{bmatrix} 2 &1 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}+3$

一个二次函数的一般形式是： $f(x)=\frac{1}{2}x^{T}Ax+b^{T}x+c$

它的一阶导 $\forall f(x)=Ax+b$ 二阶导 $\forall ^{2}f(x)=A$ ，它的二阶导就是这个二次型的矩阵A。

可视化：如果A是正定的，那么f(x)就是一个严格的凸函数（如图1），那么f(x)的极小值就是最小值，就是全局的最小值。此时最小化f(x)就等价于解一个线性方程组 $minimize.f(x)\ll =\gg Ax+b=0$ 。在优化算法和机器学习中是一个非常重要的性质，可以避免我们得到的驻点但不是全局最小值的情况，如果A不是正定的，那么f(x)就不是严格的凸函数（如图2、图3）。最小化f(x)时就会很麻烦。

正定矩阵的判定

一、验证定义

$x^{T}Ax>0,\forall x\epsilon R^{n},x\neq 0$

此方法在运算过程中可能会涉及到配方换元等，不方便，几乎不采用此方法。

可视化：从定义可知，任意一个向量x经A的变换后，再与x做点积，结果大于0，说明x经过A的变换后它与原x的夹角是小于90°的。这也正好正定矩阵对应名字中“正”的粗略含义，并没有翻折等负的操作。

二、验证特征值都大于0

对于对称矩阵，特征值都大于0与矩阵正定是等价的。证明如下：

（1）A正定，验证特征值都大于0：

取x为特征向量，则 $x^{T}Ax=x^{T}(\lambda x)=\lambda x^{T}x>0$ ，其中 $x^{T}x=x_{1}^{2}+...+x_{n}^{2}>0$ ，所以 $\lambda>0$

（2）特征值都大于0，验证A正定：

因为A是实对称阵，给A做一个正交相似对角化 $x^{T}Ax=x^{T}Q^{T}\Lambda Qx=(Qx)^{T}\Lambda (Qx)>0$ ，其中 $Qx\neq 0$ ， $\Lambda =diag(\lambda _{1},...,\lambda _{n})$ , $\lambda$ 都大于0.

要计算所以特征值比较麻烦，此方法用的少。

可视化：先说明对特征值的理解，正的特征值是这个变换在特征向量方向上的拉伸，并没有翻转。而对称矩阵的特征向量是正交的，在没有翻转的情况下，变换前后的向量不可能夹角大于90°，所以矩阵特征值都大于0时，矩阵就是正定的。

三、验证各阶主子式的行列式都大于0

各阶主子式的行列式都大于0与矩阵正定是等价的。证明如下：

（1）A正定，验证各阶主子式的行列式都大于0

（2）各阶主子式都大于0，验证A正定

可视化：行列式的几何意义是变换前后高维“体积”缩放的倍数，而特征值的几何意义是变换前后在某个方向缩放的倍数，故矩阵的行列式等于矩阵所以特征值的乘积，矩阵的行列式为正，说明矩阵特征值全为正或有偶数个负，但如果矩阵的各阶主子式都大于0，那么矩阵的特征值就全为正的。理由：n维矩阵的n-1阶主子式的特征值为（n-1）个，这（n-1）个特征值为原n维矩阵的n个特征值中的（n-1）个向（n-1）维做投影，其正负属性不变，所以当如果矩阵的各阶主子式都大于0，那么矩阵的特征值就全为正的，矩阵正定。

二次型函数

圆锥曲线判别式

对于二次型函数 $f(x,y)=ax^{2}+2bxy+cy^{2}=\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} a &b \\ b &c \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$

当 $a>0$ 时， $ac-b^{2}>0$ ，则矩阵为正定矩阵，二次型函数为正定函数（如图4）

当 $a>0$ 时， $ac-b^{2}<0$ ，则矩阵为不定矩阵，二次型函数为不定函数（如图5）

当 $a<0$ 时， $ac-b^{2}<0$ ，则矩阵为不定矩阵，二次型函数为不定函数（如图6）

当 $a<0$ 时， $ac-b^{2}>0$ ，则矩阵为负定矩阵，二次型函数为负定函数（如图7）

当 $ac-b^{2}=0$ ，则矩阵为半正定矩阵，二次型函数为半正定定函数（如图8）

图4： $f(x,y)=2x^{2}+2xy+4y^{2}$ ， $\begin{bmatrix} a & b\\ b & c \end{bmatrix}=\begin{bmatrix} 2 &1 \\ 1 &4 \end{bmatrix}$ ，正定，矩阵特征值都为正

图5： $f(x,y)=2x^{2}+8xy+4y^{2}$ ， $\begin{bmatrix} a & b\\ b & c \end{bmatrix}=\begin{bmatrix} 2 &4 \\ 4&4 \end{bmatrix}$ ，不定，矩阵特征值一正一负

图6： $f(x,y)=-2x^{2}-8xy+4y^{2}$ ， $\begin{bmatrix} a & b\\ b & c \end{bmatrix}=\begin{bmatrix} -2 &-4 \\ -4 &4 \end{bmatrix}$ ，不定，矩阵特征值一正一负

图7： $f(x,y)=-2x^{2}+2xy-4y^{2}$ ， $\begin{bmatrix} a & b\\ b & c \end{bmatrix}=\begin{bmatrix} -2 &1 \\ 1 &-4 \end{bmatrix}$ ，负定，矩阵特征值都为负

图8： $f(x,y)=2x^{2}+4xy+2y^{2}$ ， $\begin{bmatrix} a & b\\ b & c \end{bmatrix}=\begin{bmatrix} 2 &2 \\ 2 &2 \end{bmatrix}$ ，半正定，矩阵特征值含0

合同变换，正交变换

对于二次型函数 $f(x,y)=2x^{2}+2bxy+4y^{2}=\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} 2 &b \\ b &4 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}$ 中的矩阵 $\begin{bmatrix} 2 &b \\ b & 4 \end{bmatrix}$ ，