八叉树CSG布尔运算

news2024/11/15 18:03:37

1. 前言

布尔运算是几何内核的核心话题之一，又分为二维布尔运算和三维布尔运算，其中三维布尔运算技术难度较高，缘之空间维度的提升。

根据实现的理论不同，三维布尔运算又分为B-Rep布尔运算、CSG布尔运算、三角网格布尔运算等方法，其背后的理论与几何数据结构紧密联系，如B-Rep方式表达的几何体往往采用B-Rep布尔运算方法进行造型，CSG方式表达的几何体造型过程又离不开CSG布尔运算，在一些场合中又离不开三角网格布尔运算…

本文就三角网格布尔运算进行介绍。

2. 概述

三角网格布尔运算有多种理论支撑实现，比如BSP网格布尔运算方法、八叉树网格布尔运算等，同样，不同的方法有其特点及适用范围。

BSP网格布尔运算依赖于较为严格的实体规范表达，即参与运算的几何实体需要是闭合的、规整的，如果出现不闭合的几何实体，运算可能出错，比如对一颗网格化表达的树进行布尔就会出错，得到意想不到的造型效果。如果实体内部由有其他元素时也会出现上述问题，比如大坝内部有其他多种围挡等建造元素时。
图2.1：网格化表达的树

八叉树布尔运算适用性较好，缘于其较好的鲁棒性——对于不规整几何体的兼容处理能力。当然并不是说这种方法对任意网格数据均能“正确的”进行布尔运算，这里的良好的鲁棒性指的是网格数据规范的情况下，比如遵循正面的三角面索引顺序为逆时针方式等基础规范。

八叉树布尔运算应用范围较广，一些基于CSG方式表达的几何内核采用CSG-OctTree网格布尔运算，当然基于B-Rep方式表达的几何内核也可以采用八叉树布尔运算，根据其需要。（如果OCC支持网格布尔运算，会有很多人大喜之）

3. 内容

3.1 八叉树表达

需要将参与运算的几何实体进行八叉树空间划分和归属，这里有一些技巧。
图3.1.1：meshA构造的八叉树
图3.1.2：meshB构造的八叉树

上图中叶子节点为什么大小不一样？不同节点由于其所涉及的三角面数量不一样，进行了不同程度的细化，也可以说是自适应细化。

3.2 标记传递

几何实体将空间分割，叶子节点被区分为几何体内（in）、几何体外（out）、几何体切割（cut）三种情况，而cut情况进一步的得到parts in& parts out，聪明的你大概已经知道接下来要怎么做了，那将是下节内容要讲的。怎么知道是该标记为in、out、cut呢？

首先我们知道树叶子节点为cut的情况，简单来说就是有三角面“经过”该叶子节点所处空间时，此叶子节点即被标记为cut，进而我们标记了所有cut类型的叶子节点；

对标记为cut的叶子节点进行切割，得出parts in& parts out部分，进一步可以标记所处空间的6个面（将其标记为in、out或cut），这里的面标记非常重要，它是标记传递的源动力；

下面以meshB对应的八叉树为例进行说明，
图3.2.1：标记为cut的叶子节点中的“part in”部分

由标记为cut的叶子节点出发进行标记传递，即由其空间的6个面进行出发进行面标记传递，相邻空间的相邻面是标记传递的对象；一般来说可以这样进行传递：由cut类型的叶子节点出发标记其兄弟姐妹（另外7个叶子节点），进一步和其兄弟姐妹一起共同标记他们的父节点；

这样一颗八叉树表达的网格实体被标记完成，所有的节点（叶子节点及祖先节点）均被进行了有效标记。也就是我们得到了整个全覆盖空间的标记，试想，如果给你一个三角面，是否可以快速判断它是在这个八叉树空间中是in、out或cut？聪明的你已经想到了，可以用被标记的八叉树去“切割”另一颗八叉树，无论其有没有被标记！我们将在下一节中继续娓娓道来。
图3.2.2：标记为cut的叶子节点切割三角面

图3.2.3：标记为in的叶子节点
图3.2.4：标记为out的叶子节点（视图1）

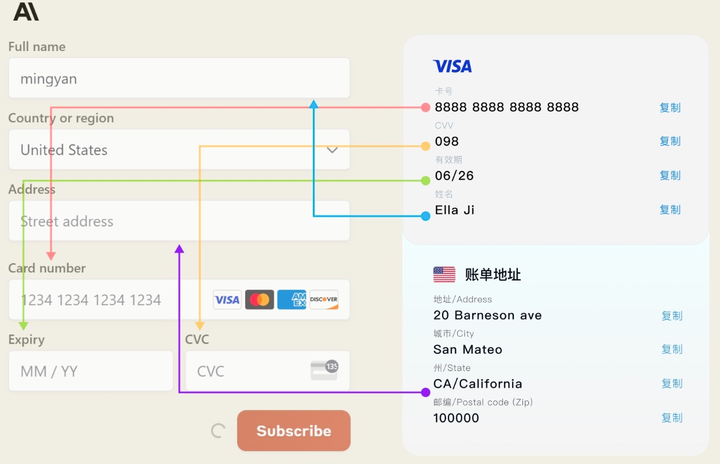
我们从底部来看下标记为out的叶子节点，
图3.2.5：标记为out的叶子节点（视图2）

当然此过程有很多细节需要去考虑，有一些处理技巧，由于篇幅所限（作者懒~），不再展开。

我们来看整体效果，

meshA构造的八叉树如下，
图3.2.6：被标记的八叉树（meshA构造）

meshA构造的八叉树在标记后的效果如下，
图3.2.7：被标记的八叉树（meshA构造）
图3.2.8：被标记的八叉树（meshB构造）
图3.2.9：被标记的八叉树（meshB构造）

3.3 布尔运算

对于参数布尔运算的网格实体meshA和meshB，经过上述过程，我们得到了两颗对应的八叉树octTreeA和octTreeB，且它们均被成功标记；

octTreeA切割octTreeB，可以得到meshB在meshA中的部分（meshA_out_meshB）、meshB在meshA外的部分(meshA_in_meshB)；
同样用octTreeB切割octTreeA，我们可以得到meshB_out_meshA、meshB_in_meshA；

这就是布尔运算的过程。

3.4 获取结果

不知不觉就来到了获取结果的阶段，怎么获取结果呢？如果你有一定的几何理论基础，你可能已经知道答案了。

对上述四部分进⾏组合即可得到交、并、差结果。如求交运算为将meshA_in_meshB和meshB_in_meshA组合，A减B运算为先将meshB_in_meshA取反，再与meshA_out_meshB组合。

表3.4.1 运算结果

运算类型	组合	备注
A∩B	“meshA_in_meshB” + “meshB_in_meshA”
A∪B	“meshA_out_meshB” + “meshB_out_meshA”
A-B	“meshA_out_meshB” + ~“meshB_in_meshA”	~为取反，此处为取反面
B-A	“meshB_out_meshA” + ~“meshA_in_meshB”	~为取反，此处为取反面